The standard potential of the following cell is 0.23 V at and at .
(i) write the cell reaction .
(ii) Calculate and for the cell reaction by assuming that these quantities remain unchanged in the range to .
(iii) calculate the solubility of in water at .
Give , the standard reduction potential of the is 0.80 V at .
To solve the given problem step by step, we will break it down into three parts as specified in the question.
Part (i): Write the cell reaction.
1. Identify the half-reactions:
- At the anode (oxidation):
12H2→H++e−
- At the cathode (reduction):
AgCl+e−→Ag+Cl−
2. Combine the half-reactions:
- The overall cell reaction can be written by combining the two half-reactions:
12H2+AgCl→H++Ag+Cl−
Part (ii): Calculate ΔH∘ and ΔS∘ for the cell reaction.
1. Use the relationship between Gibbs free energy, enthalpy, and entropy:
ΔG∘=ΔH∘−TΔS∘
We also know that:
ΔG∘=−nFEcell
where n is the number of moles of electrons transferred, F is Faraday's constant (96500 C/mol), and Ecell is the cell potential.
2. Calculate ΔG∘ at both temperatures:
- For 15∘C (288 K):
ΔG∘15=−nF⋅Ecell=−1⋅96500⋅0.23=−22219.5J
- For 35∘C (308 K):
ΔG∘35=−nF⋅Ecell=−1⋅96500⋅0.21=−20265J
3. Set up equations for ΔH∘ and ΔS∘:
- For 15∘C:
−22219.5=ΔH∘−288ΔS∘(1)
- For 35∘C:
−20265=ΔH∘−308ΔS∘(2)
4. Solve the equations simultaneously:
- Rearranging both equations gives:
ΔH∘=−22219.5+288ΔS∘(from(1))
ΔH∘=−20265+308ΔS∘(from(2))
- Set the two expressions for ΔH∘ equal to each other:
−22219.5+288ΔS∘=−20265+308ΔS∘
- Solving for ΔS∘:
−1954.5=20ΔS∘⟹ΔS∘=−97.725J/K
5. Substituting ΔS∘ back to find ΔH∘:
- Using ΔS∘ in equation (1):
ΔH∘=−22219.5+288⋅(−97.725)=49.987kJ
Part (iii): Calculate the solubility of AgCl in water at 25∘C.
1. Use the Nernst equation:
E=E∘−0.0591nlogQ
At equilibrium, E=0 and Q=Ksp:
0=E∘−0.05911logKsp
2. Substituting the standard reduction potential for Ag+:
E∘=0.80V⟹0.80=0.05911logKsp
Rearranging gives:
logKsp=0.800.0591⟹Ksp=100.800.0591≈1.47×10−10
3. Calculate the solubility:
- The solubility S of AgCl in water is given by:
Ksp=(Ag+)(Cl−)=S2⟹S=√Ksp=√1.47×10−10≈1.21×10−5mol/L
Summary of Results
- (i) Cell Reaction: 12H2+AgCl→H++Ag+Cl−
- (ii) ΔH∘≈49.987kJ, ΔS∘≈−97.725J/K
- (iii) Solubility of AgCl at 25∘C is approximately 1.21×10−5mol/L.
- At the anode (oxidation):
12H2→H++e−
- At the cathode (reduction):
AgCl+e−→Ag+Cl−
- The overall cell reaction can be written by combining the two half-reactions:
12H2+AgCl→H++Ag+Cl−
ΔG∘=ΔH∘−TΔS∘
We also know that:
ΔG∘=−nFEcell
where n is the number of moles of electrons transferred, F is Faraday's constant (96500 C/mol), and Ecell is the cell potential.
- For 15∘C (288 K):
ΔG∘15=−nF⋅Ecell=−1⋅96500⋅0.23=−22219.5J
- For 35∘C (308 K):
ΔG∘35=−nF⋅Ecell=−1⋅96500⋅0.21=−20265J
- For 15∘C:
−22219.5=ΔH∘−288ΔS∘(1)
- For 35∘C:
−20265=ΔH∘−308ΔS∘(2)
- Rearranging both equations gives:
ΔH∘=−22219.5+288ΔS∘(from(1))
ΔH∘=−20265+308ΔS∘(from(2))
- Set the two expressions for ΔH∘ equal to each other:
−22219.5+288ΔS∘=−20265+308ΔS∘
- Solving for ΔS∘:
−1954.5=20ΔS∘⟹ΔS∘=−97.725J/K
- Using ΔS∘ in equation (1):
ΔH∘=−22219.5+288⋅(−97.725)=49.987kJ
E=E∘−0.0591nlogQ
At equilibrium, E=0 and Q=Ksp:
0=E∘−0.05911logKsp
E∘=0.80V⟹0.80=0.05911logKsp
Rearranging gives:
logKsp=0.800.0591⟹Ksp=100.800.0591≈1.47×10−10
- The solubility S of AgCl in water is given by:
Ksp=(Ag+)(Cl−)=S2⟹S=√Ksp=√1.47×10−10≈1.21×10−5mol/L
- (i) Cell Reaction: 12H2+AgCl→H++Ag+Cl−
- (ii) ΔH∘≈49.987kJ, ΔS∘≈−97.725J/K
- (iii) Solubility of AgCl at 25∘C is approximately 1.21×10−5mol/L.
Topper's Solved these Questions
- ELECTROCHEMISTRY Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROCHEMISTRY Exercise:Assignment (SECTION - I) (Subjective Type Question)
Explore 12 Videos
- COORDINATION COMPOUNDS Book:AAKASH INSTITUTE ENGLISHChapter:COORDINATION COMPOUNDS Exercise:Assignment (Section-J Aakash Challenger Questions )
Explore 10 Videos
- ENVIRONMENTAL CHEMISTRYBook:AAKASH INSTITUTE ENGLISHChapter:ENVIRONMENTAL CHEMISTRYExercise:ASSIGNMENT (SECTION-D) (Assertion - Reason Type Questions)
Explore 4 Videos
Similar Questions
The standard potential of the following cell is 0.23V at 15∘C and 0.21V at 35∘C:
Pt∣H2(g)|HCl(aq)|AgCl(s)∣Ag(s)
a. Write the cell reaction.
b. Calculate ΔHc− and ΔSc− for the cell reaction by assuming that these quantities remain unchanged in the range 15∘C to 35∘C
c. Calculate the solubility of AgCl in water at 25∘C.
Given : The standard reduction potential of Ag⊕(aq)∣Ag(s) is 0.80V at 25∘C.
View SolutionThe EMF of the following cellis 1.05V at 25∘C:
Pt,H2(g)(1.0atm)|NaOH(0.1m),NaCl(0.1M)|AgCl(s),Ag(s)
a. Write the cell reaction,
b. Calculate pKw of water.
View SolutionThe EMF of the following cellis 1.05V at 25∘C:
Pt,H2(g)(1.0atm)|NaOH(0.1m),NaCl(0.1M)|AgCl(s),Ag(s)
Write the cell reaction.
View SolutionFor the cell Zn|ZnCl2(m)|AgCl,E is 1.24V at 25∘C and 1.260V at 35∘C of m=10−3. Write down the cell reaction and calculate ΔG,ΔH, and ΔS at 25∘C.
View SolutionThe emf of the following cell is 0.256 V at 25∘C and 0.2595 V at 35∘C. Calculate heat of reaction taking place at 25∘C.
Pt(H2)|HCl(aq)||AgCl|Ag
View SolutionCalculate the standard potential of the cell ,If the standard electrode potentials of Zn2+/ZnandAg+/Ag are -0.763 V and + 0.799 V respectively .
View SolutionThe EMF of Westron standard cell is 1.0153 at 20∘C and 1.01807 at 25∘C. CalculateΔG,ΔH, and ΔS for the cell reaction at 25∘C.
View SolutionThe standard potential of a cell using the reaction
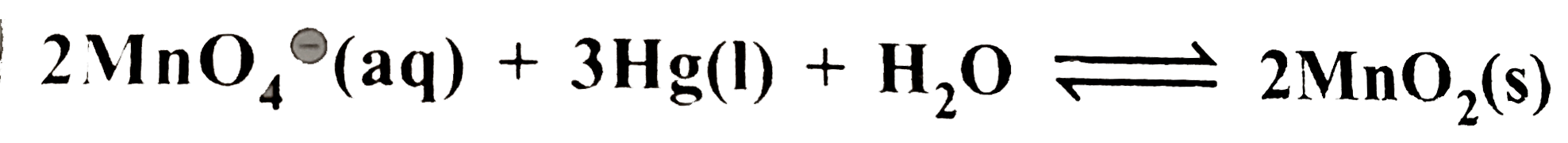 +3HgO(s)+2(c−OH)(aq) is 0.489V at 25∘C. What is the equilibrium constant of the reaction ?
+3HgO(s)+2(c−OH)(aq) is 0.489V at 25∘C. What is the equilibrium constant of the reaction ?
View SolutionCalculate the emf of the following cell at 25∘C
Ag(s)|AgNO3(0.01M)||AgNO3(0.05M)|Ag(s)
View SolutionThe standard emf of the cell, Cd(s)|CdCI2(aq)(0.1M)||AgCI(s)|Ag(s) in which the cell reaction is Cd(s)+2AgCI(s)→2Ag(s)+Cd2+(aq) is 0.6915V at 0∘C and 0.6753V at 25∘C. The ΔH of the reaction at 25∘C is,-
View Solution
