It we see the reaction of methane with halogen, the rate determining step for chlorination is, endothermic reaction of the chlorine atom with methane to form methyl radical and a molecule of HCl. So free radical is the intermediate of the reaction. Formation of free radical depends upon the energy required to break a bond between a hydrogen atom and a carbon atom. Chlorination of propane and Bromination of propane. when compared it is found that bromination is more selective than chlorination. The probability factor for 3∘,2∘,1∘H atom is 5.0:3.8:1.0 at 25∘C for chlorination.
Isobutane when reacts with chlorine in presence of ultra violet radiations yield 2 products primary hydrogen substituted and 3∘ hydrogen substituted Find their % in product mixture
64% 36%
72% 28%
36% 64%
30% 70%
The correct Answer is:A
To solve the problem of determining the percentage of primary and tertiary hydrogen substituted products when isobutane reacts with chlorine in the presence of ultraviolet radiation, we can follow these steps:
Step 1: Identify the structure of Isobutane
Isobutane (C4H10) has the following structure:
CH3|CH3−C−CH3|H
In isobutane, there are 9 primary hydrogen atoms and 1 tertiary hydrogen atom.
Step 2: Determine the probability factors
From the problem, we know the probability factors for the substitution of hydrogen atoms:
- For primary hydrogen: 1
- For tertiary hydrogen: 5
Step 3: Calculate the effective contribution of each type of hydrogen
- The total contribution from primary hydrogens:
- Number of primary hydrogens = 9
- Probability factor for primary hydrogen = 1
- Total contribution from primary hydrogens = 9 * 1 = 9
- The total contribution from tertiary hydrogen:
- Number of tertiary hydrogens = 1
- Probability factor for tertiary hydrogen = 5
- Total contribution from tertiary hydrogens = 1 * 5 = 5
Step 4: Calculate the total contributions
Now, we can find the total contributions from both types of hydrogen:
- Total contributions = Contribution from primary hydrogens + Contribution from tertiary hydrogens
- Total contributions = 9 + 5 = 14
Step 5: Calculate the percentage of each product
- Percentage of primary hydrogen substituted product (A):
\(
\text{Percentage of A} = \left(\frac{\text{Contribution from primary hydrogens}}{\text{Total contributions}}\right) \times 100 = \left(\frac{9}{14}\right) \times 100 \approx 64\%
\)
- Percentage of tertiary hydrogen substituted product (B):
\(
\text{Percentage of B} = \left(\frac{\text{Contribution from tertiary hydrogens}}{\text{Total contributions}}\right) \times 100 = \left(\frac{5}{14}\right) \times 100 \approx 36\%
\)
Conclusion
Thus, the percentages of the products formed are:
- Primary hydrogen substituted product: 64%
- Tertiary hydrogen substituted product: 36%
Final Answer
The percentages in the product mixture are 64% for the primary hydrogen substituted product and 36% for the tertiary hydrogen substituted product.
---
Isobutane (C4H10) has the following structure:
CH3|CH3−C−CH3|H
In isobutane, there are 9 primary hydrogen atoms and 1 tertiary hydrogen atom.
From the problem, we know the probability factors for the substitution of hydrogen atoms:
- For primary hydrogen: 1
- For tertiary hydrogen: 5
- The total contribution from primary hydrogens:
- Number of primary hydrogens = 9
- Probability factor for primary hydrogen = 1
- Total contribution from primary hydrogens = 9 * 1 = 9
- Number of tertiary hydrogens = 1
- Probability factor for tertiary hydrogen = 5
- Total contribution from tertiary hydrogens = 1 * 5 = 5
Now, we can find the total contributions from both types of hydrogen:
- Total contributions = Contribution from primary hydrogens + Contribution from tertiary hydrogens
- Total contributions = 9 + 5 = 14
- Percentage of primary hydrogen substituted product (A):
\(
\text{Percentage of A} = \left(\frac{\text{Contribution from primary hydrogens}}{\text{Total contributions}}\right) \times 100 = \left(\frac{9}{14}\right) \times 100 \approx 64\%
\)
\(
\text{Percentage of B} = \left(\frac{\text{Contribution from tertiary hydrogens}}{\text{Total contributions}}\right) \times 100 = \left(\frac{5}{14}\right) \times 100 \approx 36\%
\)
Thus, the percentages of the products formed are:
- Primary hydrogen substituted product: 64%
- Tertiary hydrogen substituted product: 36%
The percentages in the product mixture are 64% for the primary hydrogen substituted product and 36% for the tertiary hydrogen substituted product.
Topper's Solved these Questions
- HYDROCARBONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - HYDROCARBONSEXERCISE - SECTION-E ASSERTION-REASON TYPE QUESTIONS:
9 Videos
- HYDROCARBONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - HYDROCARBONSEXERCISE - SECTION-F MATRIX-MATCH TYPE QUESTIONS
5 Videos
- HYDROCARBONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - HYDROCARBONSEXERCISE - SECTION-C OBJECTIVE TYPE QUESTIONS (MORE THAN ONE OPTIONS ARE CORRECT)
12 Videos
- HALOALKANES AND HALOARENES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - HALOALKANES AND HALOARENES EXERCISE - ASSIGNMENT SECTION -D
15 Videos
- HYDROGENBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - HYDROGENEXERCISE - ASSIGNMENT (SECTION - D) (Assertion-Reason Type question)
15 Videos
Similar Questions
Knowledge Check
Formation of free radical is easiest in :
A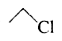 B
B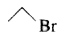 C
C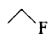 D
D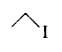
The most stable free radical is
A⋅CH3BCH3⋅CH2C(CH3)2⋅CHD(CH3)3⋅CFree radicals can undergo
Arearrangement to a more stable free radicalBdecomposition to give another free radicalCcombination with other free radicalDall are correct
Chlorination of methane proceeds by
View SolutionWhen two free radicals collide
View SolutionHunsdiecker reaction involve free radical in intermediate steps.
View SolutionHow do you account for the formation of ethane during chlorination of methane ?
View SolutionHow do you account for the formation of ethane during chlorination of methane ?
View Solution