Compound which rotates the plane polarised light is known as optically active compound . On the basis of direction of rotation two forms of an optically active compounds are termed as dextro and laevo rotatory . The two are termed as enantiomers . If we have a 1 : 1 mixture of d and l isomers of a given chiral compound , optical rotation of such mixture is zero Such a mixture is optically inactive and is called a recemic modification.
The net specific rotation of any mixture of the d and isomers of a given chiral compound is equal to the weighted average of the rotations due to both the isomers Mathematically if can be expressed as :
[α]≠t=fd[αd]+f1[αl]
Where fa and fl are fractions of d and l isomers respectively and [αd],[αl] are their specific rotations
The pure d isomer of certain chiral compound has
[α]25d=+55∘.A non racemic mixture of this compound has a net [α]25d=−11∘. What is the fractions of this isomer in mixture ?
0. 40
0.6
0.3
0. 70
The correct Answer is:1
To solve the problem, we need to find the fraction of the D isomer in a non-racemic mixture of a chiral compound, given the specific rotations of the D and L isomers and the net specific rotation of the mixture.
1. Understand the Given Data:
- Specific rotation of D isomer, (αd)=+55∘
- Specific rotation of L isomer, (αl)=−55∘ (since L is the enantiomer of D)
- Net specific rotation of the mixture, (αnet)=−11∘
2. Set Up the Fractions:
- Let the fraction of the D isomer be fD.
- Then, the fraction of the L isomer will be fL=1−fD.
3. Use the Formula for Net Specific Rotation:
- The formula for the net specific rotation is:
(αnet)=fD(αd)+fL(αl)
- Substituting the values, we get:
−11=fD(55)+(1−fD)(−55)
4. Simplify the Equation:
- Expanding the equation:
−11=55fD−55+55fD
- Combine like terms:
−11=110fD−55
5. Solve for fD:
- Rearranging gives:
110fD=−11+55
110fD=44
fD=44110=0.4
6. Conclusion:
- The fraction of the D isomer in the mixture is fD=0.4.
Final Answer:
The fraction of the D isomer in the mixture is 0.4.
- Specific rotation of D isomer, (αd)=+55∘
- Specific rotation of L isomer, (αl)=−55∘ (since L is the enantiomer of D)
- Net specific rotation of the mixture, (αnet)=−11∘
- Let the fraction of the D isomer be fD.
- Then, the fraction of the L isomer will be fL=1−fD.
- The formula for the net specific rotation is:
(αnet)=fD(αd)+fL(αl)
- Substituting the values, we get:
−11=fD(55)+(1−fD)(−55)
- Expanding the equation:
−11=55fD−55+55fD
- Combine like terms:
−11=110fD−55
- Rearranging gives:
110fD=−11+55
110fD=44
fD=44110=0.4
- The fraction of the D isomer in the mixture is fD=0.4.
The fraction of the D isomer in the mixture is 0.4.
Topper's Solved these Questions
- HALOALKANES AND HALOARENES Book:AAKASH INSTITUTE ENGLISHChapter:HALOALKANES AND HALOARENES Exercise:Assignment (Section - E) ( Assertion - Reason type Questions )
Explore 7 Videos
- HALOALKANES AND HALOARENES Book:AAKASH INSTITUTE ENGLISHChapter:HALOALKANES AND HALOARENES Exercise:Assignment (Section - F) (Matrix - Match Type Question )
Explore 4 Videos
- HALOALKANES AND HALOARENES Book:AAKASH INSTITUTE ENGLISHChapter:HALOALKANES AND HALOARENES Exercise:Assignment (Section - C ) ( Objective Type Question(More than one options are correct ))
Explore 17 Videos
- GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSBook:AAKASH INSTITUTE ENGLISHChapter:GENERAL PRINCIPLES AND PROCESSES OF ISOLATION OF ELEMENTSExercise:Try Yourself
Explore 33 Videos
- HYDROCARBONSBook:AAKASH INSTITUTE ENGLISHChapter:HYDROCARBONSExercise:Assignment(Section - C) (Previous Years Questions)
Explore 60 Videos
Similar Questions
Knowledge Check
An optically active compound
Arotates the plane of polarised lightBchanges the direction of polarised lightCdoes not allow plane polarised light to pass throughDnone of these.The compound which is optically active is :
A1-butanolB2-butanolC1-propanolD2-methyl-l-propanol
Which complex is optically active ?
View SolutionWhich of the following is optically active
View SolutionWhich of these molecule is optically active ?

View SolutionThe compounds
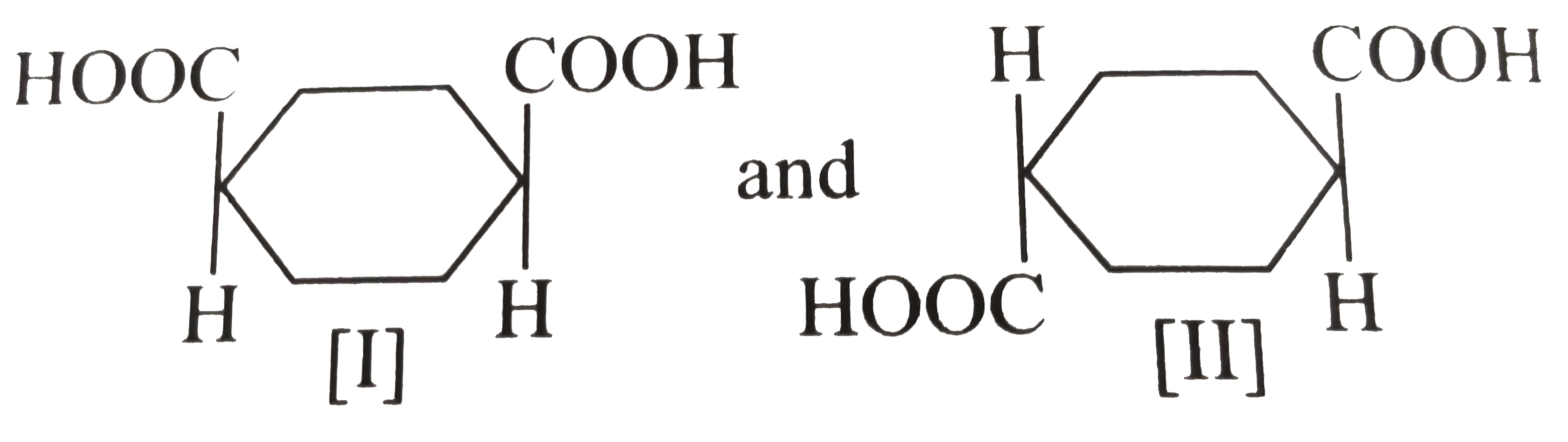
are optically inactive because
View SolutionHow is the optical rotation of an optically active compound measured and how is it expressed ?
View SolutionThe formation of an optically active compound from a chiral molecule is called:
View Solution
