Select the correct statement. For a particle moving on a straight line
Average speed is equal to magnitude of average velocity
Average speed may be greater than magnitude of average velocity
Average velocity = instantaneous velocity if velocity is constant
Moving with constant acceleration, average velocity for given time interval is arithmetic mean of initial and final velocity
The correct Answer is:B, C, D
To solve the question regarding the correct statements for a particle moving on a straight line, let's analyze each option step by step.
1. Understanding Average Speed and Average Velocity:
- Average speed is defined as the total distance traveled divided by the total time taken.
- Average velocity is defined as the total displacement divided by the total time taken.
- It is important to note that displacement is always less than or equal to distance.
2. Analyzing Option 1:
- The first option states that "average speed is equal to average velocity."
- Since average speed is greater than or equal to average velocity (due to the nature of distance and displacement), this statement is incorrect.
- Conclusion: Option 1 is incorrect.
3. Analyzing Option 2:
- The second option states that "average speed may be greater than the magnitude of average velocity."
- Given that average speed is always greater than or equal to average velocity, this statement holds true.
- Conclusion: Option 2 is correct.
4. Analyzing Option 3:
- The third option states that "average velocity is equal to instantaneous velocity if velocity is constant."
- When velocity is constant, the average velocity over any time interval is equal to the instantaneous velocity at any point in that interval.
- Therefore, this statement is also correct.
- Conclusion: Option 3 is correct.
5. Analyzing Option 4:
- The fourth option states that "moving with constant acceleration, average velocity for a given time interval is the arithmetic mean of initial and final velocity."
- For a particle moving with constant acceleration, the average velocity can be calculated as:
Average Velocity=u+v2
where v=u+at (final velocity).
- Substituting this into the equation gives:
Average Velocity=u+(u+at)2=2u+at2=u+at2
- This confirms that the average velocity is indeed the arithmetic mean of initial and final velocities.
- Conclusion: Option 4 is correct.
Final Summary:
- Correct Options: 2, 3, and 4.
- Incorrect Option: 1.
- Average speed is defined as the total distance traveled divided by the total time taken.
- Average velocity is defined as the total displacement divided by the total time taken.
- It is important to note that displacement is always less than or equal to distance.
- The first option states that "average speed is equal to average velocity."
- Since average speed is greater than or equal to average velocity (due to the nature of distance and displacement), this statement is incorrect.
- Conclusion: Option 1 is incorrect.
- The second option states that "average speed may be greater than the magnitude of average velocity."
- Given that average speed is always greater than or equal to average velocity, this statement holds true.
- Conclusion: Option 2 is correct.
- The third option states that "average velocity is equal to instantaneous velocity if velocity is constant."
- When velocity is constant, the average velocity over any time interval is equal to the instantaneous velocity at any point in that interval.
- Therefore, this statement is also correct.
- Conclusion: Option 3 is correct.
- The fourth option states that "moving with constant acceleration, average velocity for a given time interval is the arithmetic mean of initial and final velocity."
- For a particle moving with constant acceleration, the average velocity can be calculated as:
Average Velocity=u+v2
where v=u+at (final velocity).
- Substituting this into the equation gives:
Average Velocity=u+(u+at)2=2u+at2=u+at2
- This confirms that the average velocity is indeed the arithmetic mean of initial and final velocities.
- Conclusion: Option 4 is correct.
- Correct Options: 2, 3, and 4.
- Incorrect Option: 1.
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - D)
Explore 24 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - E)
Explore 8 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - B)
Explore 19 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
Similar Questions
Mark the correct statements for a particle going on a straight line:
View SolutionGraph of velocity versus displacement of a particle moving in a straight line is as shown in figure.
The acceleration of the particle is.
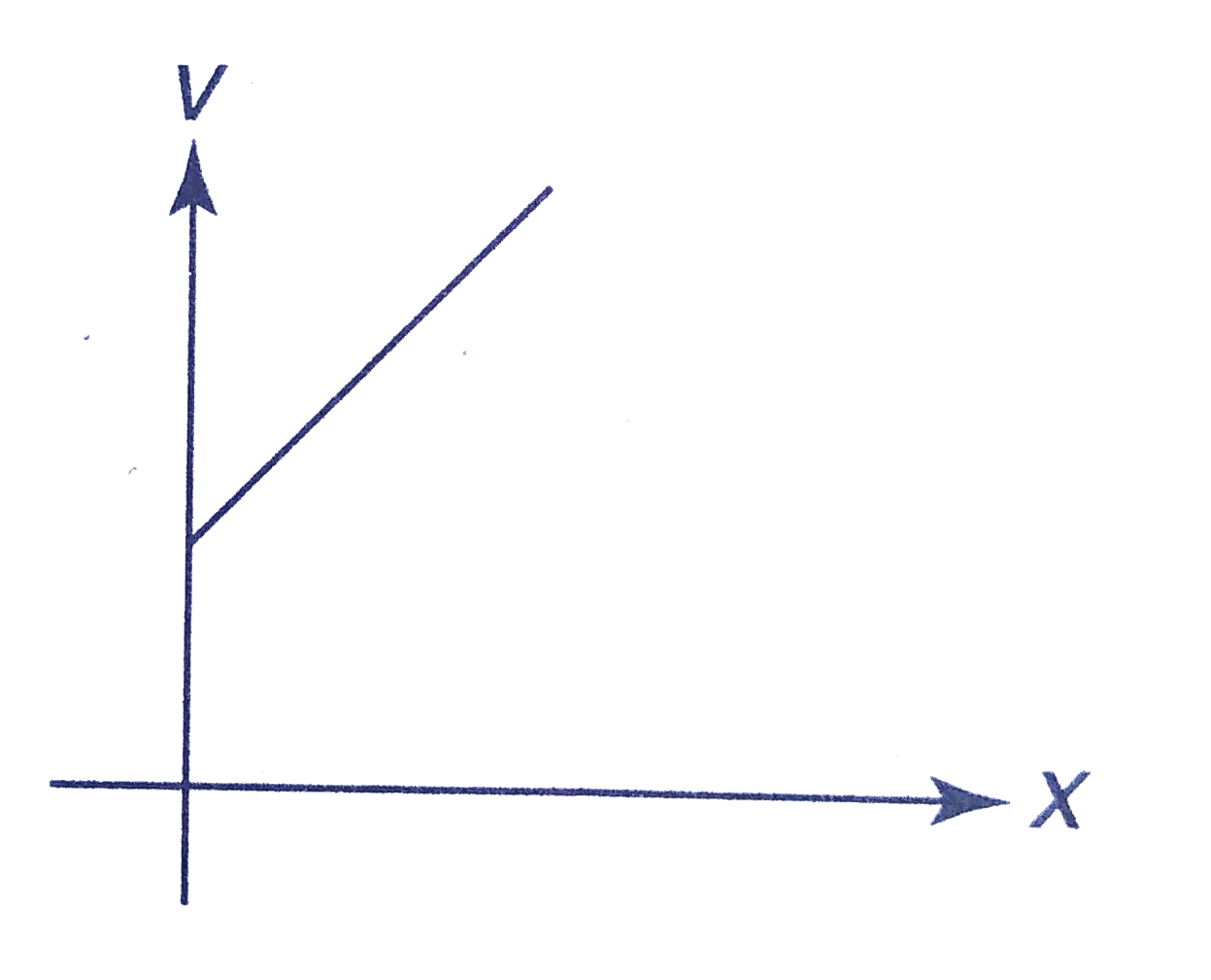
View Solution
The velcocity displacement graph of a particle moving along a straight line is shown in figure. The velocity as function of x(0≤x≤1) is
View SolutionStatement-I : A particle moves in a straight line with constant acceleration. The average velocity of this particle cannot be zero in any time interval.
Statement-II : For a particle moving in straight line with constant acceleration, the average velocity in a time interval is u+v2, where u and v are initial and final velocity of the particle of the given time interval.
View Solution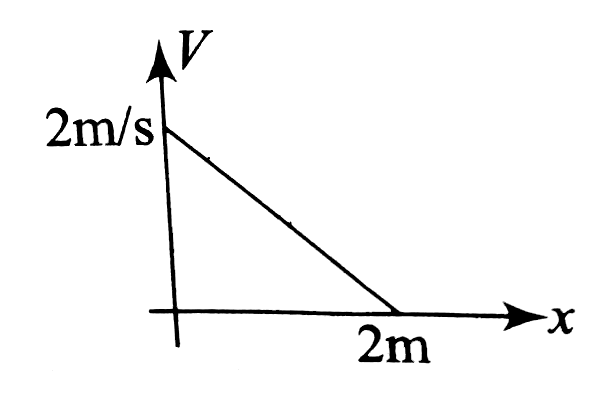
The velocity displacement graph of a particle moving along a straight line is shown in figure.
Then the acceleration displacement graph is.
View SolutionVelocity displacement graph of a particle moving in a straight line is as shown in figure.
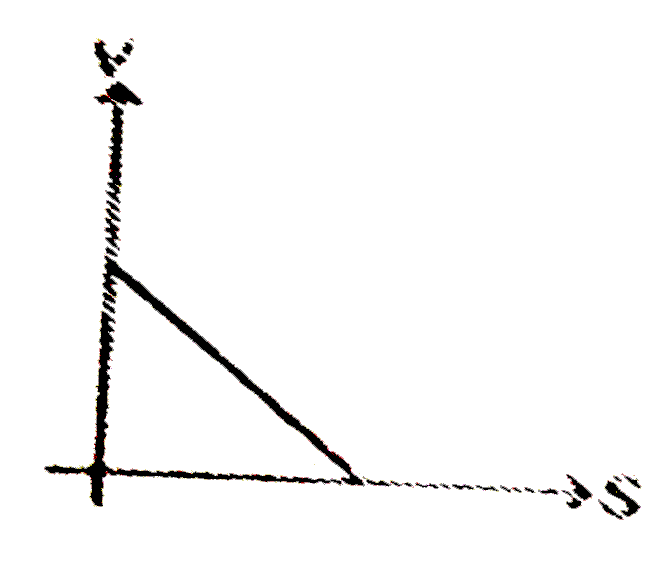
View SolutionVelocity versus displacement graph of a particle moving in a straight line as shown in figure.

The acceleration of the particle.
View SolutionVelocity versus displacement graph of a particle moving in a straight line as shown in figure.
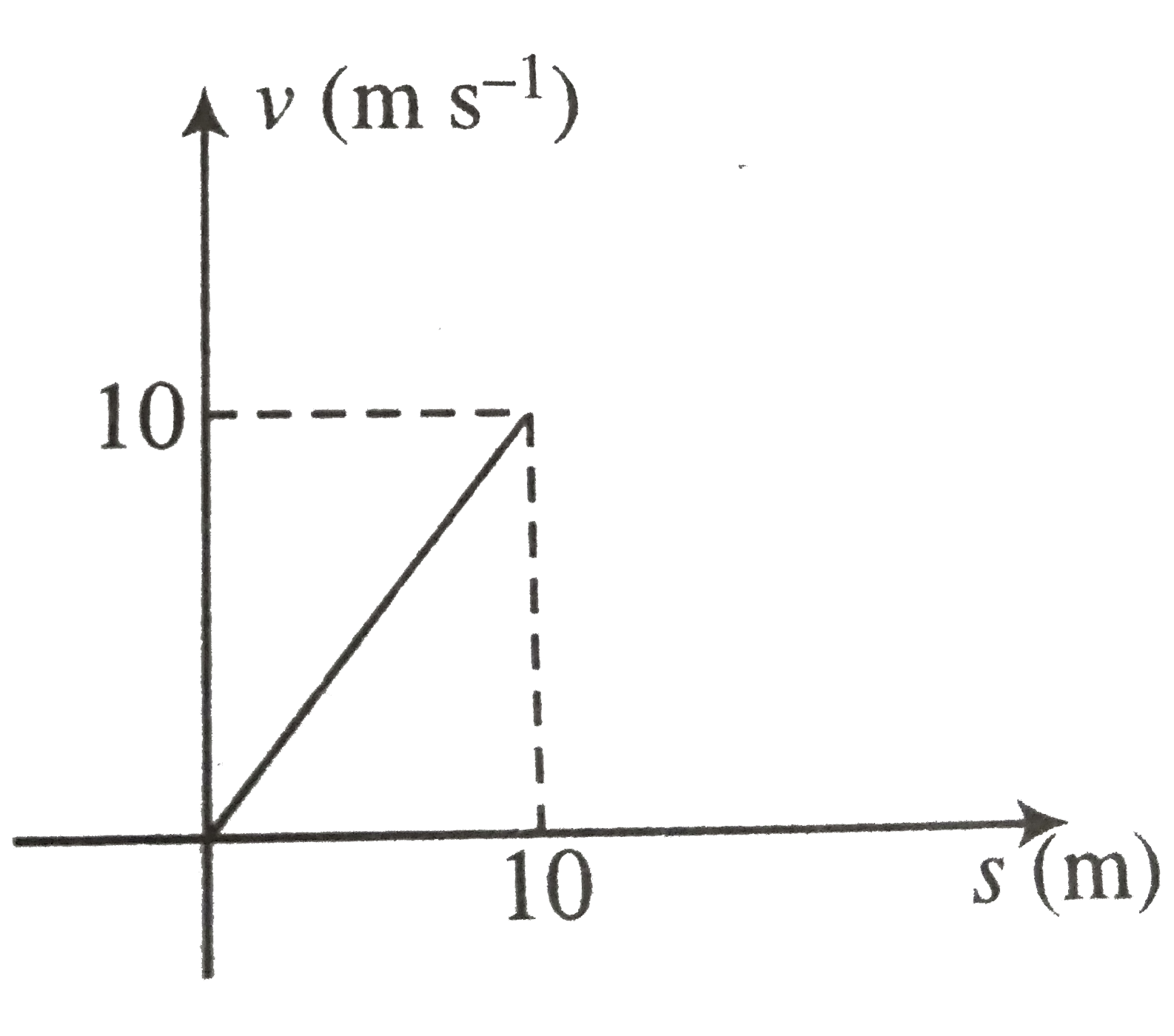
The corresponding acceleration versus velocity graph will be .
View SolutionThe velocity - displacement graph of a particle moving along a straight line is shown
The most suitable acceleration - displacement graph will be

View SolutionThe graph of displacement vs time for a particle moving along a straight line is as shown. The best option for the corresponding velocity - time graph will be:
View Solution