STATEMENT - 1 : Distance travelled by a particle moving rectilinearly may not be equal to magnitude of displacement of the particle.
and
STATEMENT - 2 : Distance travelled is a scalar but displacement is a vector.
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-2
Statement-1 is True, Statement-2 is True, Statement-2 is NOT a correct explanation for Statement-2
Statement-1 is True, Statement-2 is False
Statement-1 is False, Statement-2 is True
The correct Answer is:B
To solve the given problem, we need to analyze the two statements provided and determine their validity and relationship.
1. Understanding Distance and Displacement:
- Distance is defined as the total path length traveled by an object, regardless of direction. It is a scalar quantity, meaning it has magnitude but no direction.
- Displacement is defined as the shortest straight-line distance from the initial position to the final position of the object. It is a vector quantity, meaning it has both magnitude and direction.
2. Evaluating Statement 1:
- The first statement claims that "Distance travelled by a particle moving rectilinearly may not be equal to the magnitude of displacement of the particle."
- This statement is true. For example, if a particle moves from point A to point B and then returns to point C, the distance traveled is the total length of the path (AB + BC), while the displacement is the straight-line distance from point A to point C. In this case, the distance traveled is greater than the magnitude of displacement.
3. Evaluating Statement 2:
- The second statement claims that "Distance travelled is a scalar but displacement is a vector."
- This statement is also true. As previously mentioned, distance is a scalar quantity and displacement is a vector quantity.
4. Determining the Relationship Between the Statements:
- Both statements are true, but we need to check if Statement 2 is the correct explanation for Statement 1.
- While both statements are true, the fact that distance is a scalar and displacement is a vector does not directly explain why distance may not equal displacement. The relationship between distance and displacement is based on the path taken, not solely on their scalar and vector nature.
5. Conclusion:
- Since both statements are true but Statement 2 does not provide a correct explanation for Statement 1, the correct answer is that both statements are true, but Statement 2 is not the correct explanation of Statement 1.
Final Answer:
The correct option is B: Both statements are true, but Statement 2 is not the correct explanation of Statement 1.
- Distance is defined as the total path length traveled by an object, regardless of direction. It is a scalar quantity, meaning it has magnitude but no direction.
- Displacement is defined as the shortest straight-line distance from the initial position to the final position of the object. It is a vector quantity, meaning it has both magnitude and direction.
- The first statement claims that "Distance travelled by a particle moving rectilinearly may not be equal to the magnitude of displacement of the particle."
- This statement is true. For example, if a particle moves from point A to point B and then returns to point C, the distance traveled is the total length of the path (AB + BC), while the displacement is the straight-line distance from point A to point C. In this case, the distance traveled is greater than the magnitude of displacement.
- The second statement claims that "Distance travelled is a scalar but displacement is a vector."
- This statement is also true. As previously mentioned, distance is a scalar quantity and displacement is a vector quantity.
- Both statements are true, but we need to check if Statement 2 is the correct explanation for Statement 1.
- While both statements are true, the fact that distance is a scalar and displacement is a vector does not directly explain why distance may not equal displacement. The relationship between distance and displacement is based on the path taken, not solely on their scalar and vector nature.
- Since both statements are true but Statement 2 does not provide a correct explanation for Statement 1, the correct answer is that both statements are true, but Statement 2 is not the correct explanation of Statement 1.
The correct option is B: Both statements are true, but Statement 2 is not the correct explanation of Statement 1.
Topper's Solved these Questions
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - F)
Explore 2 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - G)
Explore 4 Videos
- MOTION IN STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN STRAIGHT LINEExercise:Assignment (SECTION - D)
Explore 24 Videos
- MOTION IN A STRAIGHT LINEBook:AAKASH INSTITUTE ENGLISHChapter:MOTION IN A STRAIGHT LINEExercise:ASSIGNMENT (SECTION - D)
Explore 15 Videos
- MOVING CHARGE AND MAGNESIUMBook:AAKASH INSTITUTE ENGLISHChapter:MOVING CHARGE AND MAGNESIUMExercise:SECTION D
Explore 16 Videos
Similar Questions
When is the magnitude of displacement equal to the distance ?
View SolutionVelocity time graph for a particle moving in a line is given.
Calculate the displacement of the particle and distance travelled in first 4 seconds.
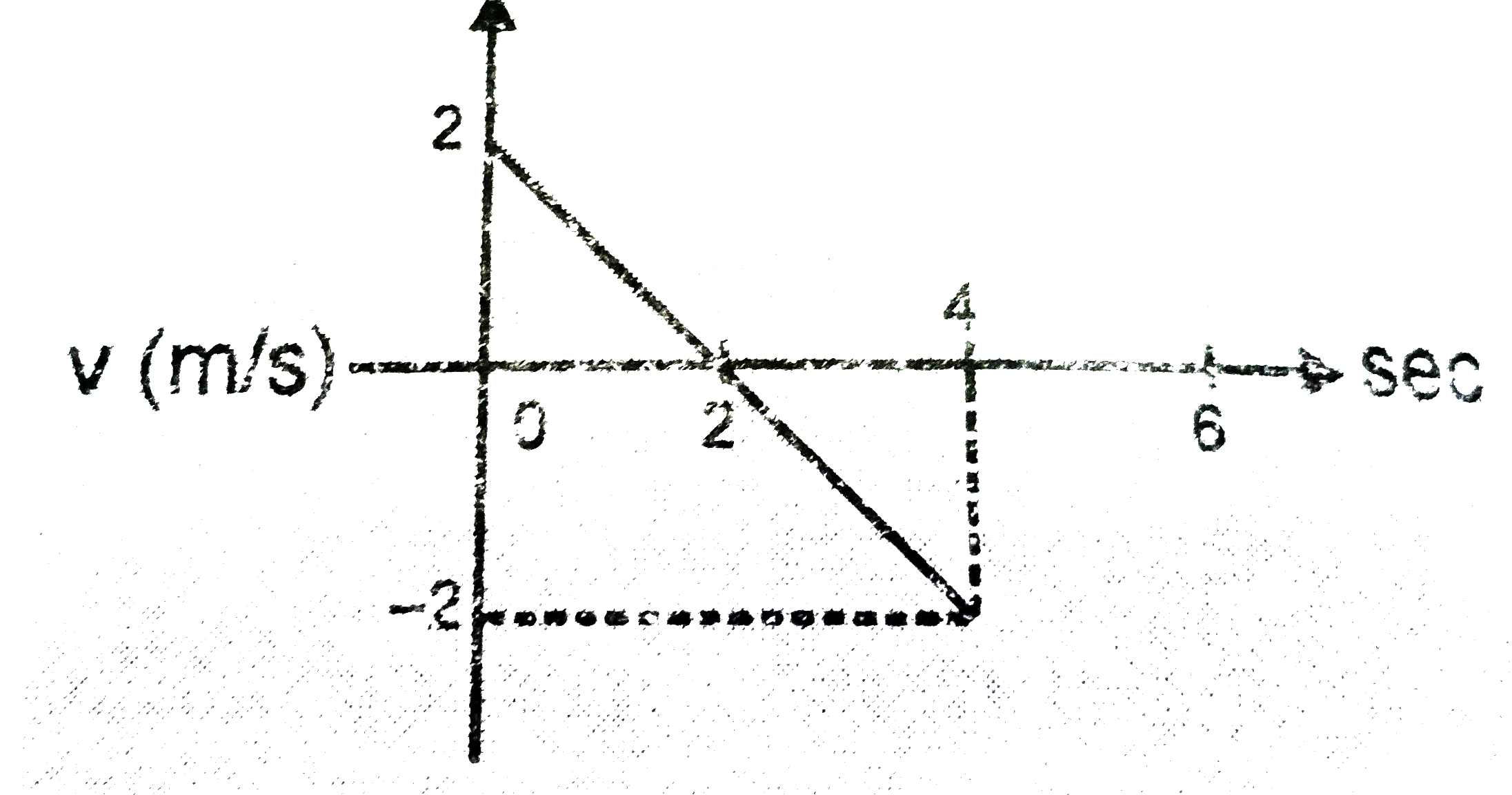
View SolutionThe distance travelled by a particle is proportional to the squares of time, then the particle travels with
View SolutionIf the displacement of a particle is zero, then distance covered by it
View SolutionIf the displacement of a particle is zero, then distance covered by it
View SolutionA particle moves along a path ABCD as shown in the figure. Then the magnitude of net displacement of the particle from position A to D is:

View SolutionA particle travels from A to B path shown in figure, then the displacement of particle is :
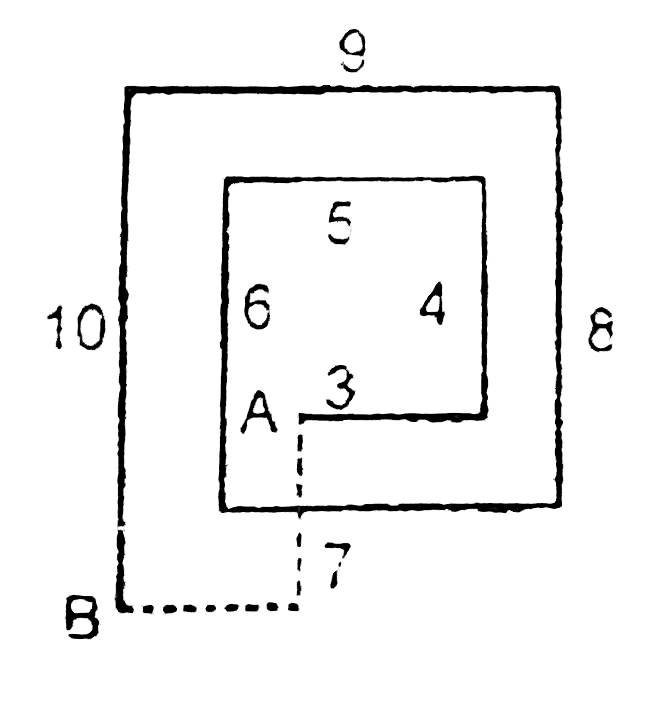 .
.
View SolutionIf distance coverd by a particle is zero , what can be its displacement ?
View SolutionThe distance travelled by a particle in a straight line motion is directly proportional to t1/2, where t is the time elapsed.
View SolutionIn which of the following cases of motions, the distance moved and the magnitude of displacement are equal ?
View Solution
