A small stone of mass 0.4 kg tied to a massless inextensible string is made to loop the loop Radius of the path is 4 m. Find its speed at the highest point. How would this speed change if mass of the stone is decoreased by 10%?(g=10ms−2).
To solve the problem, we will follow these steps:
Step 1: Understand the problem
We have a small stone of mass 0.4 kg tied to a massless inextensible string, making it loop in a circular path with a radius of 4 m. We need to find the speed of the stone at the highest point of the loop.
Step 2: Identify the relevant formula
In circular motion, the speed v at the highest point of a loop can be determined using the formula:
v=√g⋅r
where:
- g is the acceleration due to gravity (10 m/s²),
- r is the radius of the circular path (4 m).
Step 3: Substitute the values into the formula
Now, we substitute the values into the formula:
v=√10⋅4
Step 4: Calculate the speed
Calculating the expression:
v=√40
v≈6.32m/s
Step 5: Analyze the effect of mass change
Next, we need to determine how the speed changes if the mass of the stone is decreased by 10%.
From the formula v=√g⋅r, we can see that the speed does not depend on the mass of the stone. Therefore, even if the mass decreases, the speed at the highest point remains the same.
Final Answer
The speed of the stone at the highest point is approximately 6.32m/s, and it does not change if the mass is decreased by 10%.
---
We have a small stone of mass 0.4 kg tied to a massless inextensible string, making it loop in a circular path with a radius of 4 m. We need to find the speed of the stone at the highest point of the loop.
In circular motion, the speed v at the highest point of a loop can be determined using the formula:
v=√g⋅r
where:
- g is the acceleration due to gravity (10 m/s²),
- r is the radius of the circular path (4 m).
Now, we substitute the values into the formula:
v=√10⋅4
Calculating the expression:
v=√40
v≈6.32m/s
Next, we need to determine how the speed changes if the mass of the stone is decreased by 10%.
The speed of the stone at the highest point is approximately 6.32m/s, and it does not change if the mass is decreased by 10%.
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - IILUSTRATION2videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - TRY YOURSELF95videos
WORK, ENERGY AND POWER
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))12videos
WAVES
Similar Questions
Two particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
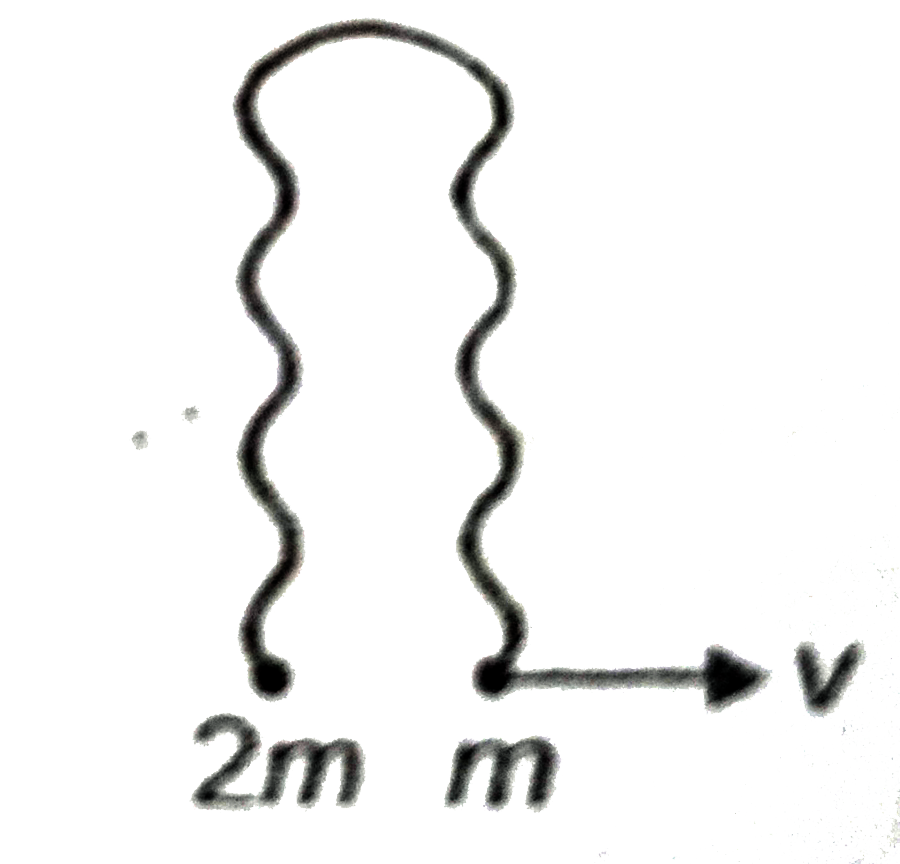 View Solution
View SolutionTwo particles of a mass 2m and m are tied with an inextensible string the particle of mass m is given a speed V as shown in the figure. Find the speed with which the particle of mass 2m starts moving.
 View Solution
View SolutionA ball of mass 0.6kg attached to a light inextensible string rotates in a vertical circle of radius 0.75m such that it has speed of 5ms−1 when the string is horizontal. Tension in the string when it is horizontal on other side is (g=10ms−2).
View SolutionA particle of mass 200 g is moving in a circle of radius 2 m. The particle is just looping the loop. The speed of the particle and the tension in the string at highest point of the circule path are (g=10ms−2)
View SolutionA particle of mass 200 g is moving in a circle of radius 2 m. The particle is just looping the loop. The speed of the particle and the tension in the string at highest point of the circule path are (g=10ms−2)
View SolutionA massless, inextensible string of length 1 m has a breaking strength of 1 kg wt. A stone of mass 0.2 kg tied to one end of the string is made to move in a vertical circle. Can the stone describe the vertical circle? (g=10ms−2)
View SolutionA small stone of mass 100 g in rotated I a verticlal circle of radius 40 cm. What is the minimum speed needed at the lowest point for looping the loop? Also find the tension in the string at this point (g=10ms−2).
View SolutionA stone of mass 1kg is tied with a string and it is whirled in a vertical circle of radius 1 m. If tension at the highest point is 14 N, then velocity at lowest point will be
View SolutionA particle of mass 100 g tied to a string is rotated along the circle of radius 0.5 m. The breaking tension of the string is 10 N. The maximum speed with which particle can be rotated without breaking the string is
View SolutionA stone of mass 0.3kg attched to a 1.5m long stirng is whirled around in a horizontal cirlcle at a speed of 6 m/s The tension in the string is
View Solution

