A particle of mass m initially at rest. A variabl force acts on the particle f=kx2 where k is a constant and x is the displacment. Find the work done by the force f when the speed of particles is v.
12kx2
12kv2
12mv2
2mv2
The correct Answer is:C
To solve the problem step by step, we will follow the outlined reasoning in the video transcript and derive the work done by the variable force f=kx2 when the speed of the particle is v.
Step 1: Understand the Given Information
- The mass of the particle is m.
- The force acting on the particle is given by f=kx2, where k is a constant and x is the displacement.
- The particle starts from rest, so the initial velocity u=0.
- We need to find the work done by the force when the speed of the particle is v.
Hint: Identify the initial conditions and the relationship between force, mass, and acceleration.
Step 2: Relate Force to Acceleration
Using Newton's second law, we can write:
f=ma
Substituting the expression for force:
kx2=ma
From this, we can express acceleration a as:
a=kx2m
Hint: Recall that acceleration can also be expressed as the derivative of velocity with respect to time.
Step 3: Express Acceleration in Terms of Velocity
We know that acceleration a can also be expressed as:
a=dvdt=dvdx⋅dxdt=vdvdx
Setting the two expressions for acceleration equal gives:
kx2m=vdvdx
Hint: This step involves using the chain rule of calculus to relate acceleration, velocity, and displacement.
Step 4: Rearranging the Equation
Rearranging the equation gives:
kx2mdx=vdv
Hint: This is a differential equation that can be integrated to find the relationship between x and v.
Step 5: Integrate Both Sides
Integrating both sides, we have:
∫kx2mdx=∫vdv
The left side integrates to:
kx33m
The right side integrates to:
v22
Thus, we have:
kx33m=v22
Hint: Make sure to set the limits of integration correctly based on the initial and final conditions.
Step 6: Solve for x3
Rearranging gives:
kx3=3mv22
So,
x3=3mv22k
Hint: This expression will help us find the work done by the force.
Step 7: Calculate the Work Done
The work done W by the force is given by:
W=∫Fdx=∫kx2dx
Evaluating this integral from 0 to x:
W=(kx33)x0=kx33
Substituting x3 from the previous step:
W=k3(3mv22k)=mv22
Hint: The work done can be expressed in terms of the final speed of the particle.
Final Result
Thus, the work done by the force when the speed of the particle is v is:
W=mv22
Conclusion: The work done by the force f when the speed of the particle is v is mv22.
- The mass of the particle is m.
- The force acting on the particle is given by f=kx2, where k is a constant and x is the displacement.
- The particle starts from rest, so the initial velocity u=0.
- We need to find the work done by the force when the speed of the particle is v.
Using Newton's second law, we can write:
f=ma
Substituting the expression for force:
kx2=ma
From this, we can express acceleration a as:
a=kx2m
We know that acceleration a can also be expressed as:
a=dvdt=dvdx⋅dxdt=vdvdx
Setting the two expressions for acceleration equal gives:
kx2m=vdvdx
Rearranging the equation gives:
kx2mdx=vdv
Integrating both sides, we have:
∫kx2mdx=∫vdv
The left side integrates to:
kx33m
The right side integrates to:
v22
Thus, we have:
kx33m=v22
Rearranging gives:
kx3=3mv22
So,
x3=3mv22k
The work done W by the force is given by:
W=∫Fdx=∫kx2dx
Evaluating this integral from 0 to x:
W=(kx33)x0=kx33
Substituting x3 from the previous step:
W=k3(3mv22k)=mv22
Thus, the work done by the force when the speed of the particle is v is:
W=mv22
Topper's Solved these Questions
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-C (OBJECTIVE TYPE QUESTIONS) (MORE THAN ONE OPTIONS ARE CORRECT)
16 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-D (LINKED COMPREHENSION TYPE QUESTIONS) (COMPREHENSION-I)
3 Videos
- WORK, ENERGY AND POWERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WORK, ENERGY AND POWEREXERCISE - SECTION-A (OBJECTIVE TYPE QUESTIONS (ONE OPTIONISCORRECT)
60 Videos
- WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVESEXERCISE - ASSIGNMENT ( SECTION-D ( Assertion - Reason Type Questions ))
12 Videos
Similar Questions
A particle of mass m initially moving with speed v.A force acts on the particle f=kx where x is the distance travelled by the particle and k is constant. Find the speed of the particle when the work done by the force equals W.
View SolutionA force F=(2+x) acts on a particle in x-direction where F is in newton and x in meter. Find the work done by this force during a displacement from 1. 0 m to x = 2.0 m.
View SolutionA force F=(2+x) acts on a particle in x-direction where F is in newton and x in metre. Find the work done by this force during a displacement form 1. 0 m to x = 2.0 m.
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in newtown and x is meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionA force F=(5+2x) acts on a particle in x direction where F is in Newtown and x is in meter. Find the work done by this force during displacement from x=0 to x=1m.
View SolutionA force F=a+bx acts on a particle in x-direction, where a and b are constants. Find the work done by this force during the displacement from x1 to x2.
View SolutionForce acting on a particle varies with displacement as shown in figure. Find the total work done by the force.
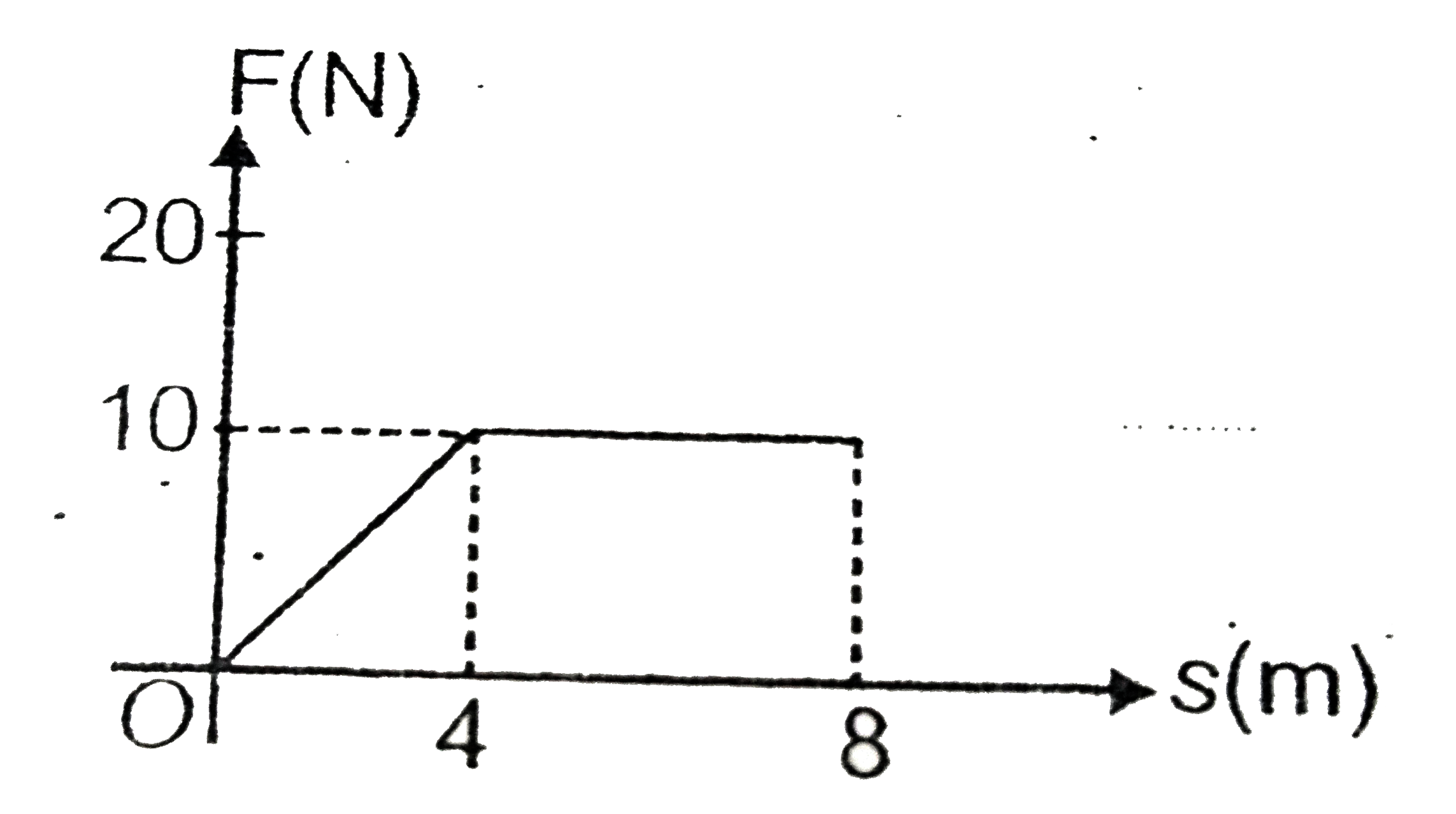
View SolutionA force F acting on a particle varies with the position x as shown in figure. Find the work done by this force in displacing the particle from

View SolutionA force F=(10+0.50x) acts on a particle in the x direction, where F is in newton and x in meter. Find the work done by this force during a displacement form x=0 to x=2.0m
View SolutionForce acting on a particle varies with displacement as shown is Fig. Find the work done by this force on the particle from x=−4m to x = + 4m.
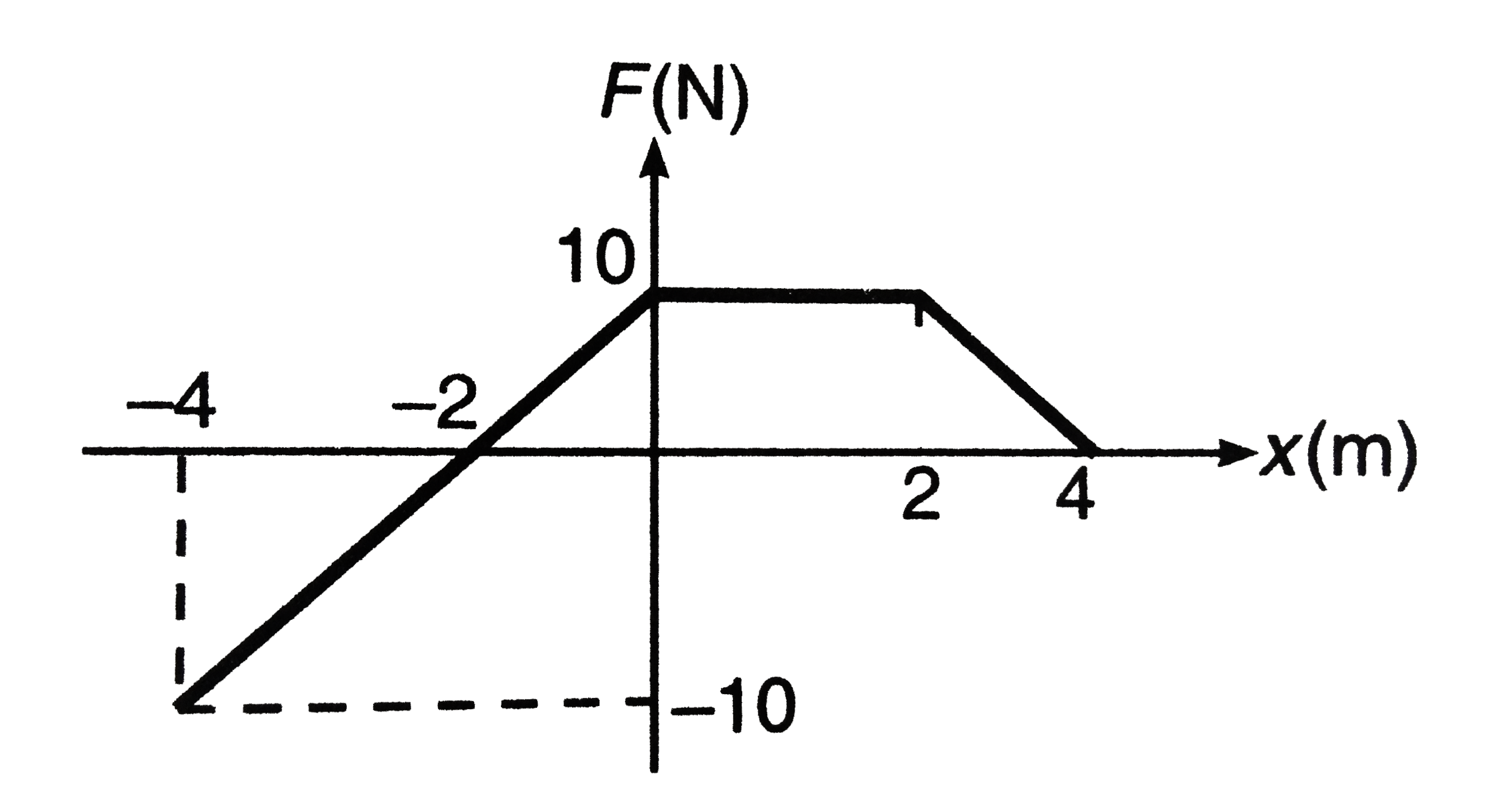 .
.
View Solution