A spherical black body of radius n radiates power p and its rate of cooling is R. then.
p∝n
p∝n2
R∝n2
R∝1n
The correct Answer is:B, D
To solve the problem, we need to analyze the relationships involving the power radiated by a spherical black body and its rate of cooling.
1. Understanding the Power Radiated:
The power radiated by a black body is given by the Stefan-Boltzmann Law:
P=σA(T4−T40)
where P is the power, σ is the Stefan-Boltzmann constant, A is the surface area of the body, T is the temperature of the body, and T0 is the temperature of the surroundings.
2. Calculating the Surface Area:
The surface area A of a sphere with radius n is:
A=4πn2
3. Substituting the Area into the Power Equation:
Substituting the expression for A into the power equation gives:
P=σ(4πn2)(T4−T40)
This can be simplified to:
P=4πσn2(T4−T40)
4. Finding the Relationship of Power with Radius:
If we consider T and T0 as constants, we can conclude that:
P∝n2
This means that the power radiated is proportional to the square of the radius of the sphere.
5. Understanding the Rate of Cooling:
The rate of cooling R can be expressed as:
R=dTdt=Pmc
where m is the mass of the body and c is the specific heat capacity.
6. Calculating the Mass:
The mass m of the spherical body can be expressed as:
m=ρV=ρ(43πn3)
where ρ is the density of the material.
7. Substituting Mass into the Rate of Cooling:
Substituting m into the rate of cooling equation gives:
R=Pρ(43πn3)c
8. Substituting Power into the Rate of Cooling:
We can substitute the expression for P into the rate of cooling:
R=4πσn2(T4−T40)ρ(43πn3)c
Simplifying this expression leads to:
R=3σ(T4−T40)ρcn
9. Finding the Relationship of Rate of Cooling with Radius:
From the above equation, we can see that:
R∝1n
This indicates that the rate of cooling is inversely proportional to the radius of the sphere.
Conclusion:
- The power radiated P is proportional to n2.
- The rate of cooling R is inversely proportional to n.
The power radiated by a black body is given by the Stefan-Boltzmann Law:
P=σA(T4−T40)
where P is the power, σ is the Stefan-Boltzmann constant, A is the surface area of the body, T is the temperature of the body, and T0 is the temperature of the surroundings.
The surface area A of a sphere with radius n is:
A=4πn2
Substituting the expression for A into the power equation gives:
P=σ(4πn2)(T4−T40)
This can be simplified to:
P=4πσn2(T4−T40)
If we consider T and T0 as constants, we can conclude that:
P∝n2
This means that the power radiated is proportional to the square of the radius of the sphere.
The rate of cooling R can be expressed as:
R=dTdt=Pmc
where m is the mass of the body and c is the specific heat capacity.
The mass m of the spherical body can be expressed as:
m=ρV=ρ(43πn3)
where ρ is the density of the material.
Substituting m into the rate of cooling equation gives:
R=Pρ(43πn3)c
We can substitute the expression for P into the rate of cooling:
R=4πσn2(T4−T40)ρ(43πn3)c
Simplifying this expression leads to:
R=3σ(T4−T40)ρcn
From the above equation, we can see that:
R∝1n
This indicates that the rate of cooling is inversely proportional to the radius of the sphere.
- The power radiated P is proportional to n2.
- The rate of cooling R is inversely proportional to n.
Topper's Solved these Questions
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-D) Linked Comprehension Type Questions
9 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-E) Assertion & Reason Type Question
10 Videos
- THERMAL PROPERTIES OF MATTERBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMAL PROPERTIES OF MATTEREXERCISE - Assignment (Section-B) Objective Type questions (one option is correct)
15 Videos
- TEST2BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TEST2EXERCISE - EXERCISE
2 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
Similar Questions
A spherical solid blakc body of radius 'r' radiates power 'H' and its rate of cooling is 'C'. If density is constant then which of the following is/are true.
View SolutionA spherical black body with radius 12 cm radiates 450 w power at 500 K. If the radius is halved and the temperature doubled, the power radiated in watts would be
View SolutionA spherical black body with radius 12 cm radiates 640 w power at 500 K. If the radius is halved and the temperature doubled, the power radiated in watts would be
View SolutionA spherical black body with a radius of 12 cm radiates 450 watt power at 500 K. If the radius were halved and the temperature doubled, the power radiated in watt would be
View SolutionA spherical black body with a radius of 12 cm radiates 450 W power at 500 K. If the radius were halved and the temperature doubled, the power radiated in watt would be
(a)225 (b)450
(c) 900 (d)1800
View SolutionThe radiations emitted by the sun are analyzeed and the spectral energy distribution curve is plotted. as shown. The radius of the sun is R, the earth is situated a distance 'd' from the sun. Treat the sun as perfectly black body which radiates power at constant rate fill till its store of hydrogen gets exhausted. (Stefan's constant =σ, Wien's constant =b, speed of light =c)
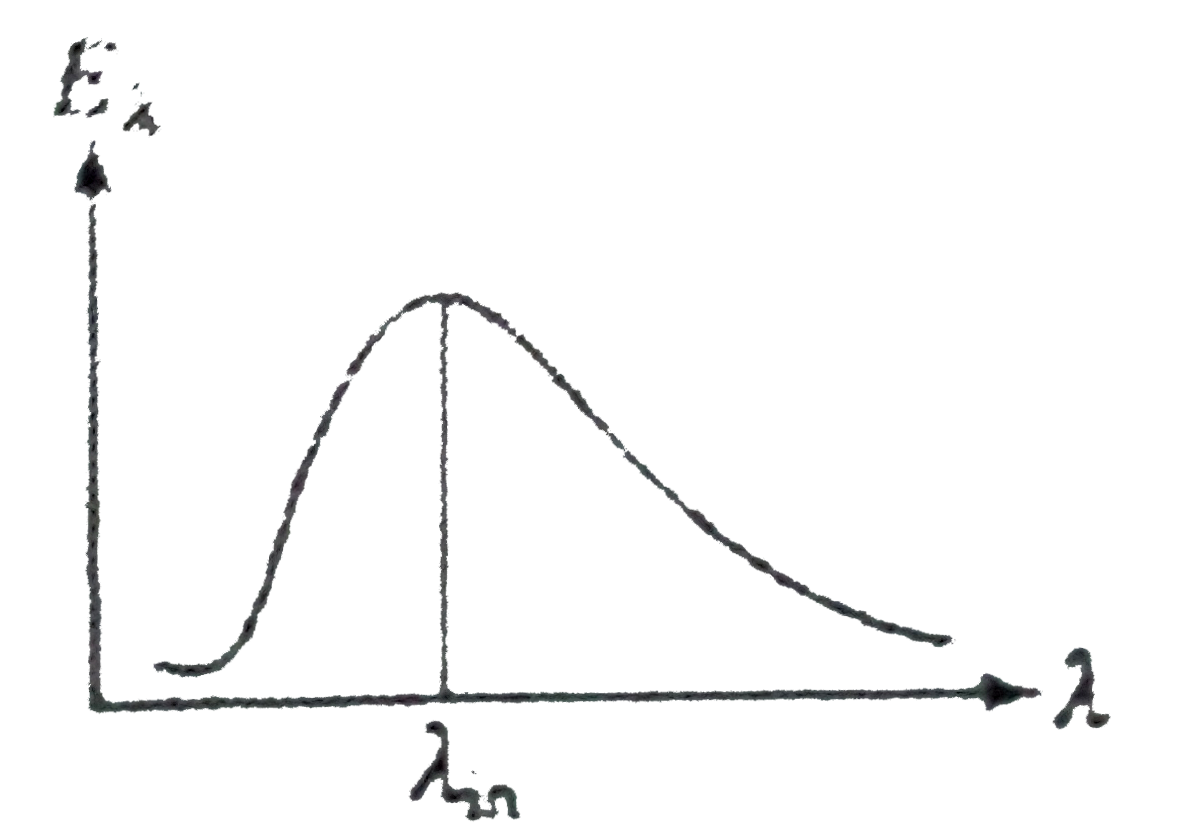
If the earth is at a distance 'd' from the sun the intensity of light falling on the earth (called solar constant S) is
View SolutionA spherical body of radius 10cm radiates 300W at 227°C. If the radius is doubled and temperature is remain same, the power radiated will be
View SolutionA spherical body of radius R consists of a fluid of constant density and is in equilibrium under its own gravity. If P(r) is the pressure at r (r < R), then the correct option(s) is (are)
View SolutionA spherical body of radius R rolls on a horizontal surface with linear velociltly v. Let L1 and L2 be the magnitudes of angular momenta of the body about centre of mass and point of contact P. Then:
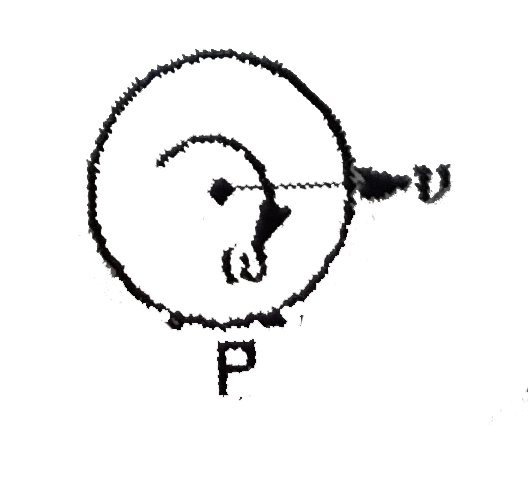
View SolutionThe temperature at which a black body of unit area loses its energy at the rate of 1 joule/second is
View Solution
