A beam of protons is deflected sideways. Could this deflection be caused
(1) By an electric field ?
(2) By a magnetic field ?
(3) If either could be responsible how would you be able to tell which was present ?
To solve the question, we will analyze the effects of electric and magnetic fields on a beam of protons and determine how to distinguish between the two.
1. Understanding the Deflection of Protons:
- A beam of protons is a stream of positively charged particles. When they move through an electric or magnetic field, they experience a force that can cause them to deflect.
2. Deflection by an Electric Field:
- When a charged particle, such as a proton, enters an electric field (E), it experiences a force given by the equation:
F=qE
where q is the charge of the proton. This force acts in the direction of the electric field.
- Therefore, the protons will be deflected in the direction of the electric field. Thus, an electric field can indeed cause the beam of protons to deflect sideways.
3. Deflection by a Magnetic Field:
- When a charged particle moves through a magnetic field (B) with a velocity (v), it experiences a magnetic force given by:
F=q(v×B)
This force is perpendicular to both the velocity of the particle and the magnetic field direction, following the right-hand rule.
- Hence, a magnetic field can also cause the protons to deflect sideways, but the direction of the deflection depends on the orientation of the magnetic field relative to the velocity of the protons.
4. Distinguishing Between Electric and Magnetic Fields:
- To determine which field is causing the deflection, we can change the direction of the proton beam:
- If the beam is deflected in the same direction regardless of its velocity direction, the cause is an electric field. This is because the electric force depends only on the charge and the electric field direction.
- If the direction of deflection changes when the direction of the proton beam is altered, the cause is a magnetic field. This is because the magnetic force depends on the cross product of the velocity and the magnetic field direction.
Conclusion:
1. Yes, an electric field can deflect the beam of protons.
2. Yes, a magnetic field can also deflect the beam of protons.
3. To distinguish between the two, observe the deflection behavior when the direction of the proton beam is changed.
- A beam of protons is a stream of positively charged particles. When they move through an electric or magnetic field, they experience a force that can cause them to deflect.
- When a charged particle, such as a proton, enters an electric field (E), it experiences a force given by the equation:
F=qE
where q is the charge of the proton. This force acts in the direction of the electric field.
- Therefore, the protons will be deflected in the direction of the electric field. Thus, an electric field can indeed cause the beam of protons to deflect sideways.
- When a charged particle moves through a magnetic field (B) with a velocity (v), it experiences a magnetic force given by:
F=q(v×B)
This force is perpendicular to both the velocity of the particle and the magnetic field direction, following the right-hand rule.
- Hence, a magnetic field can also cause the protons to deflect sideways, but the direction of the deflection depends on the orientation of the magnetic field relative to the velocity of the protons.
- To determine which field is causing the deflection, we can change the direction of the proton beam:
- If the beam is deflected in the same direction regardless of its velocity direction, the cause is an electric field. This is because the electric force depends only on the charge and the electric field direction.
- If the direction of deflection changes when the direction of the proton beam is altered, the cause is a magnetic field. This is because the magnetic force depends on the cross product of the velocity and the magnetic field direction.
1. Yes, an electric field can deflect the beam of protons.
2. Yes, a magnetic field can also deflect the beam of protons.
3. To distinguish between the two, observe the deflection behavior when the direction of the proton beam is changed.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself
27 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment (Section A) Objective Type Questions (One option is correct)
55 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section J (Aakash Challengers Questions)
5 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
An electron beam projected along positive x-axis deflects along the positive y-axis. If this deflection is caused by a magnetic field, what is the direction of the field?
View SolutionAn electron beam projected along the positive x-axis deflects along the positive y-axis deflects . If this deflection is caused by a magnetic field, what is the direction of the field? Can we conclude that is parallel to the z-axis?
View SolutionIt is observed that:
gamma rays are not deflected by either an electric or a magnetic field. Explain observations.
View SolutionAn electron (mass =9.1×10−31kg, charge =1.6×10−19C) experiences no deflection if subjected to an electric field of 3.2x105Vm, and a magnetic fields of 2.0×10−3Wbm2. Both the fields are normal to the path of electron and to each other. If the electric field is removed, then the electron will revolve in an orbit of radius
View SolutionAn electron (mass =9.1×10−31kg, charge =1.6×10−19C) experiences no deflection if subjected to an electric field of 3.2x105Vm, and a magnetic fields of 2.0×10−3Wbm2. Both the fields are normal to the path of electron and to each other. If the electric field is removed, then the electron will revolve in an orbit of radius
View SolutionA current i, indicated by the crosses in figure, is established in a strip of copper of height h and width w. A uniform field of magnetic induction B is applied at right angle to the strip.
(a) Calculate the drift velocity vd of the electrons.
(b) What are the magnitude and direction of the magnetic force F acting on the electrons?
(c) What should the magnitude and direction of a homogeneous electric field E be in order to counterbalance the effect of mangetic field?
(d) Calculate voltage V necessary between two sides of the conductor in order to creat this field E Between which sides of the conductor would this voltage have to be applied?
(e) If no electric field is applied from the outside, the electrons will be pushed somewhat to one side and therefore will give rise to a uniform electric field EH across the conductor until the forces of this electrostatic field EH balance the magnetic forces encountered in part (b). What will be the magnitude and direction of field EH?
Assume that n, the number of conductor electrons per unit volume is 1.1×1029m−3,h=0.02m,w=0.1cm,i=50A,andB=2T.

View SolutionA beam of cathode rays is subjected to crossed electric (E ) and magnetic fields (B). The fields are adjusted such that the beam is not deflected. The specific charge of the cathode rays is given by
View SolutionA proton beam is going from north to south and an electron beam is going from south to north. Neglecting the earth's magnetic field, the electron beam will be deflected
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
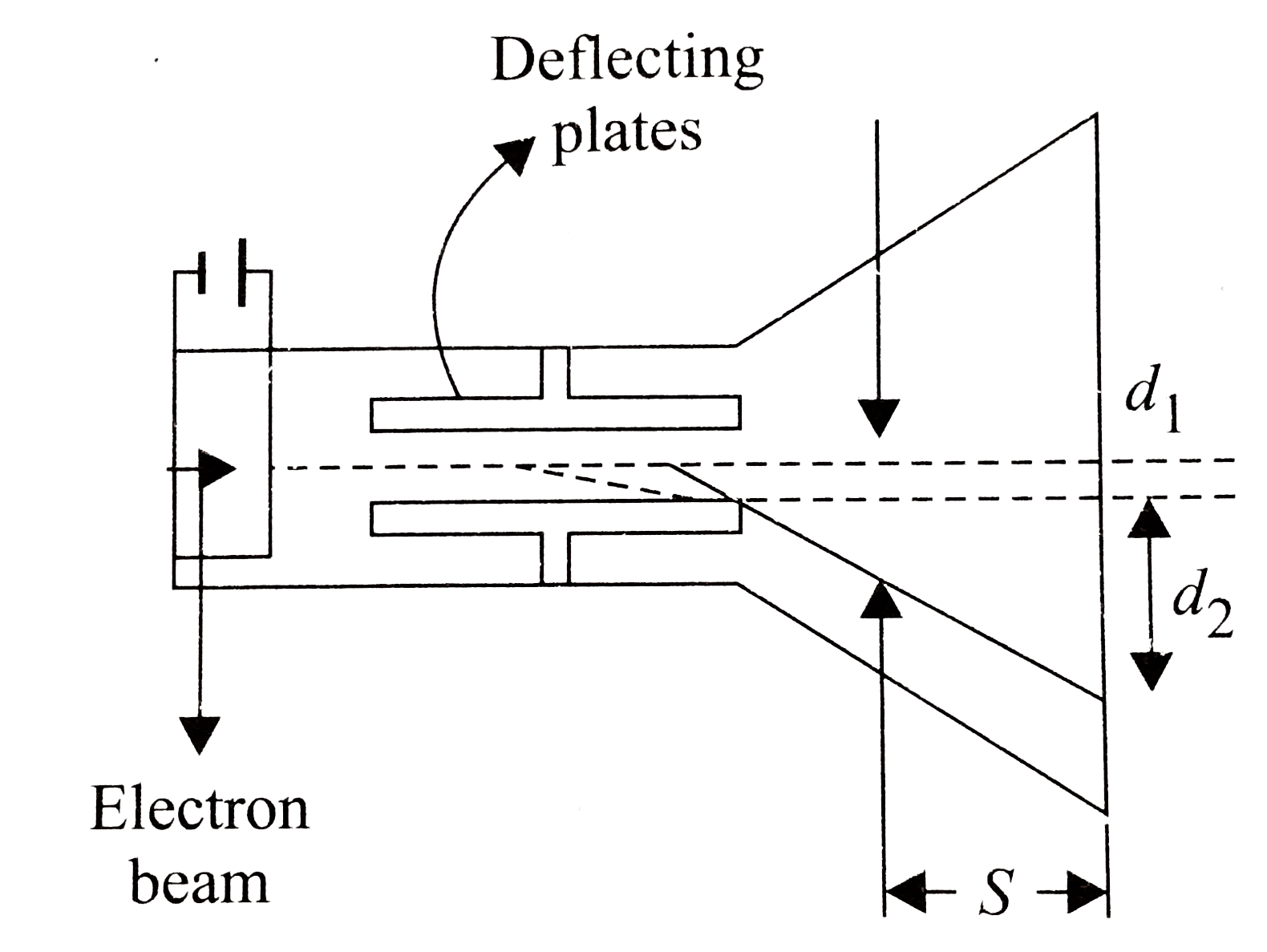
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE=evB. Using expression for d1 we can find out em=2d1EB2L2
A beam of electron with velocity 3×107ms−1 is deflected 2 mm while passing through 10 cm in an electric field of 1800V/m perpendicular to its path. e/m for electron is
View SolutionFollowing experiment was performed by J.J. Thomson in order to measure ratio of charge e and mass m of electron.
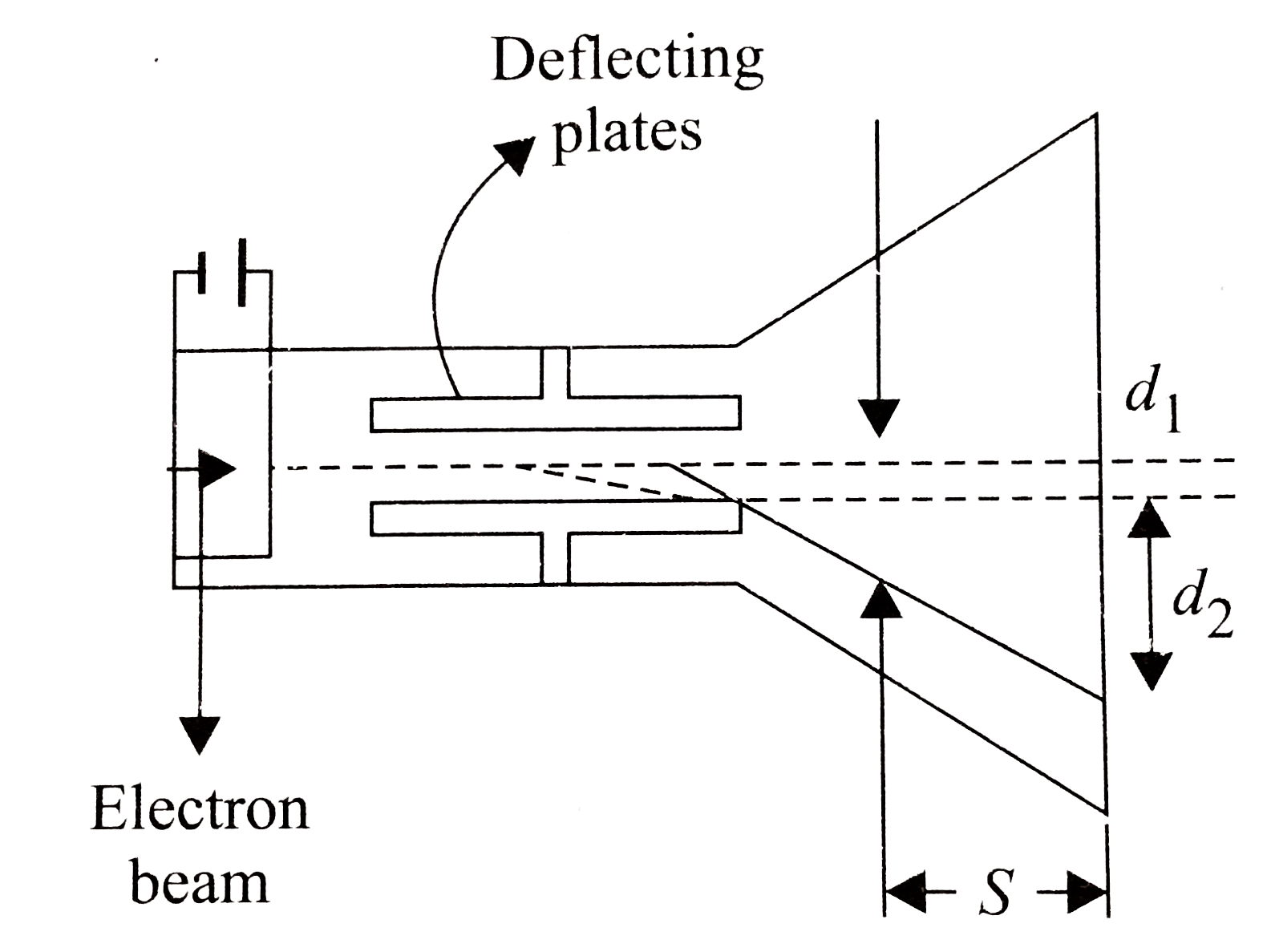
Electrons emitted from a hot filament are accelerated by a potential difference V. As the electrons pass through deflecting plates, they encounter both electric and magnetic fields. the entire region in which electrons leave the plates they enters a field free region that extends to fluorescent screen. The entire region in which electrons travel is evacuated.
Firstly, electric and magnetic fields were made zero and position of undeflected electron beam on the screen was noted. The electric field was turned on and resulting deflection was noted. Deflection is given by d1=eEL22mV2 where L = length of deflecting plate and v = speed of electron.
In second part of experiment, magnetic field was adjusted so as to exactly cancel the electric force leaving the electron beam undeflected. This gives eE = evB. Using expression for d1 we can find out em=2d1EB2L2
If the electron is deflected downward when only electric field is turned on, in what direction do the electric and magnetic fields point in second part of experiment
View Solution
