A conducting circular loop of radiius r carries a constant current i. It is placed in a uniform magnetic field →B0 such that →B0 is perpendicular to the plane of the loop . The magnetic force acting on the loop is
irB0
2πirB0
zero
πirB0
The correct Answer is:C
To solve the problem of finding the magnetic force acting on a conducting circular loop carrying a constant current in a uniform magnetic field, we can follow these steps:
1. Understand the Setup:
- We have a circular loop of radius r carrying a constant current I.
- The magnetic field →B0 is uniform and perpendicular to the plane of the loop.
2. Identify the Force on a Differential Element:
- Consider a small segment of the loop, denoted as dL, where the current I flows.
- The magnetic force dF on this differential segment in a magnetic field is given by the formula:
dF=IdL×→B
- Here, dL is the length of the differential segment and →B is the magnetic field.
3. Determine the Direction of the Force:
- The direction of the force can be determined using the right-hand rule.
- If we point the fingers of our right hand in the direction of the current (along dL) and curl them towards the magnetic field →B, the thumb will point in the direction of the force dF.
4. Calculate the Total Force:
- Since the loop is circular, we can consider the forces acting on opposite segments of the loop.
- For a segment at one point on the loop, there is an equal and opposite segment directly across the loop.
- The forces on these two segments will be equal in magnitude but opposite in direction, leading to cancellation.
5. Conclusion:
- Since every pair of diametrically opposite segments experiences equal and opposite forces, the net force acting on the entire loop is zero:
Fnet=0
Final Answer:
The magnetic force acting on the conducting circular loop is zero.
---
- We have a circular loop of radius r carrying a constant current I.
- The magnetic field →B0 is uniform and perpendicular to the plane of the loop.
- Consider a small segment of the loop, denoted as dL, where the current I flows.
- The magnetic force dF on this differential segment in a magnetic field is given by the formula:
dF=IdL×→B
- Here, dL is the length of the differential segment and →B is the magnetic field.
- The direction of the force can be determined using the right-hand rule.
- If we point the fingers of our right hand in the direction of the current (along dL) and curl them towards the magnetic field →B, the thumb will point in the direction of the force dF.
- Since the loop is circular, we can consider the forces acting on opposite segments of the loop.
- For a segment at one point on the loop, there is an equal and opposite segment directly across the loop.
- The forces on these two segments will be equal in magnitude but opposite in direction, leading to cancellation.
- Since every pair of diametrically opposite segments experiences equal and opposite forces, the net force acting on the entire loop is zero:
Fnet=0
The magnetic force acting on the conducting circular loop is zero.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment (Section B) Objective Type Questions (One option is correct)
35 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section C (Objective Type Questions (More than one option are correct)
14 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Try Yourself
27 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Knowledge Check
A conducting circular loop of radius r carries a constant current i. It is placed in a uniform magnetic field B such that B is perpendicular to the plane of loop. What is the magnetic force acting on the loop?
AI r BB2πrIBCzeroDπrIB
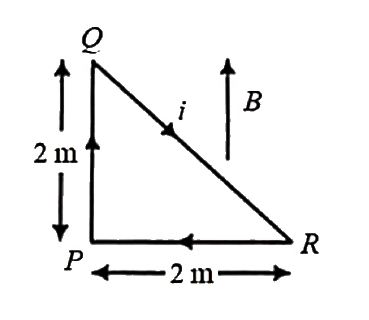
A loop PQR carries a current i=2A as shown in the figure. A uniform magnetic field B = 2T exists in space parallel to the plane of the loop . The magnetic torque on the loop is
View SolutionA current carrying loop in a uniform magnetic field will experience
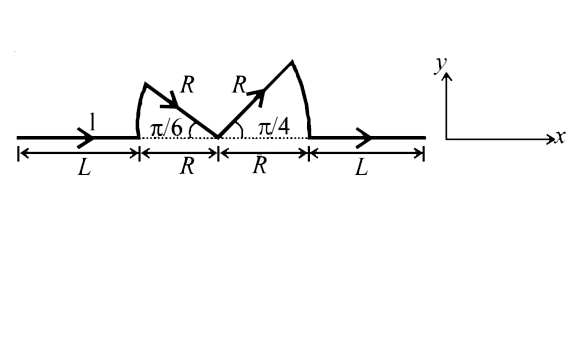
View SolutionA conductor (shown in the figure) carrying constant current I is kept in the x−y plane in a uniform magnetic field →B. If →F is the magnitude of the total magnetic force acting on the conductor, then the correct statement(s) is (are)
View SolutionA loop of Irregular shape made of flexible conducting wire carrying clockwise current is placed in uniform inward magnetic field, such that its plane is perpendicular to the field. Then the loop
View SolutionA circular loop of area 1cm2 , carrying a current of 10 A , is placed in a magnetic field of 0.1 T perpendicular to the plane of the loop. The torque on the loop due to the magnetic field is
View SolutionA non planar closed loop of arbitrary shape carryign a current I is placed in uniform magnetic field. The force acting on the loop
View SolutionA triangular loop of side l carries a current I. It is placed in a magnetic field B such that the plane of the loop is in the direction of B. The torque on the loop is
View Solution