Statement-1 A current carrying wire is placed parallel to magnetic field. The force on it due the magnetic field is zero
Statement-2 The net charge on current wire is zero
Statement-1 is True, Statement-2 is True, Statement-2 is a correct explanation for Statement-1
Statement-1 is True, Statement-2, is True, Statement-2 is NOT a correct explanation for Statement-1
Statement-1 is True, Statement-2 is False
Statement-1 is False, Statement-2 is True
The correct Answer is:B
To solve the question, we will analyze both statements and determine their validity.
1. Understanding Statement 1:
- Statement 1 claims that a current-carrying wire placed parallel to a magnetic field experiences zero force.
- The force F on a current-carrying wire in a magnetic field is given by the formula:
F=I⋅L⋅B⋅sin(θ)
where:
- I is the current,
- L is the length of the wire,
- B is the magnetic field strength,
- θ is the angle between the direction of the current and the magnetic field.
2. Analyzing the Angle:
- If the wire is parallel to the magnetic field, the angle θ is 0∘.
- The sine of 0∘ is 0:
sin(0∘)=0
- Therefore, substituting θ=0 into the force equation:
F=I⋅L⋅B⋅0=0
- This confirms that the force on the wire is indeed zero when it is parallel to the magnetic field.
3. Conclusion for Statement 1:
- Statement 1 is true.
4. Understanding Statement 2:
- Statement 2 claims that the net charge on a current-carrying wire is zero.
- In a current-carrying wire, the current is due to the flow of charge carriers (usually electrons).
- While electrons move, the overall charge of the wire remains neutral because the number of positive charges (atomic nuclei) and negative charges (electrons) are equal.
5. Conclusion for Statement 2:
- Since the wire remains electrically neutral despite the movement of charge carriers, Statement 2 is also true.
6. Evaluating the Relationship:
- Although both statements are true, Statement 2 does not explain why the force on the wire is zero when placed parallel to the magnetic field. The force being zero is due to the angle between the current and the magnetic field, not because the net charge is zero.
Final Conclusion:
- Both statements are true, but Statement 2 is not the correct explanation for Statement 1. Therefore, the correct answer is that Statement 1 is true, Statement 2 is true, but Statement 2 is not the correct explanation for Statement 1.
- Statement 1 claims that a current-carrying wire placed parallel to a magnetic field experiences zero force.
- The force F on a current-carrying wire in a magnetic field is given by the formula:
F=I⋅L⋅B⋅sin(θ)
where:
- I is the current,
- L is the length of the wire,
- B is the magnetic field strength,
- θ is the angle between the direction of the current and the magnetic field.
- If the wire is parallel to the magnetic field, the angle θ is 0∘.
- The sine of 0∘ is 0:
sin(0∘)=0
- Therefore, substituting θ=0 into the force equation:
F=I⋅L⋅B⋅0=0
- This confirms that the force on the wire is indeed zero when it is parallel to the magnetic field.
- Statement 1 is true.
- Statement 2 claims that the net charge on a current-carrying wire is zero.
- In a current-carrying wire, the current is due to the flow of charge carriers (usually electrons).
- While electrons move, the overall charge of the wire remains neutral because the number of positive charges (atomic nuclei) and negative charges (electrons) are equal.
- Since the wire remains electrically neutral despite the movement of charge carriers, Statement 2 is also true.
- Although both statements are true, Statement 2 does not explain why the force on the wire is zero when placed parallel to the magnetic field. The force being zero is due to the angle between the current and the magnetic field, not because the net charge is zero.
- Both statements are true, but Statement 2 is not the correct explanation for Statement 1. Therefore, the correct answer is that Statement 1 is true, Statement 2 is true, but Statement 2 is not the correct explanation for Statement 1.
Topper's Solved these Questions
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section F (Matrix-Match Type Questions
6 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section G Integer Answer Type Questions
2 Videos
- MOVING CHARGES AND MAGNETISMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGES AND MAGNETISMEXERCISE - Assignment Section D (Linked Comprehension Type Questions)
10 Videos
- MOVING CHARGE AND MAGNESIUMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOVING CHARGE AND MAGNESIUMEXERCISE - SECTION D
16 Videos
- NUCLEIBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - NUCLEIEXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
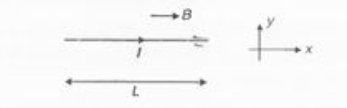
the force on current carrying wire placed in uniform magnetic field B as shown in figure is
View SolutionA long current carrying wire is bent as shown. The magnetic field induction at O is

View SolutionThe net charge in a current carrying wire is zero. Them, why does a magnetic field exert a force on it?
View SolutionThe magnetic field in a straight current carrying conductor wire is:
View SolutionThe magnetic field at the origin due to the current flowing in the wire is

View SolutionThe magnetic field at the origin due to the current flowing in the wire is

View SolutionConsider the magnetic field produced by a finitely long current carrying wire .
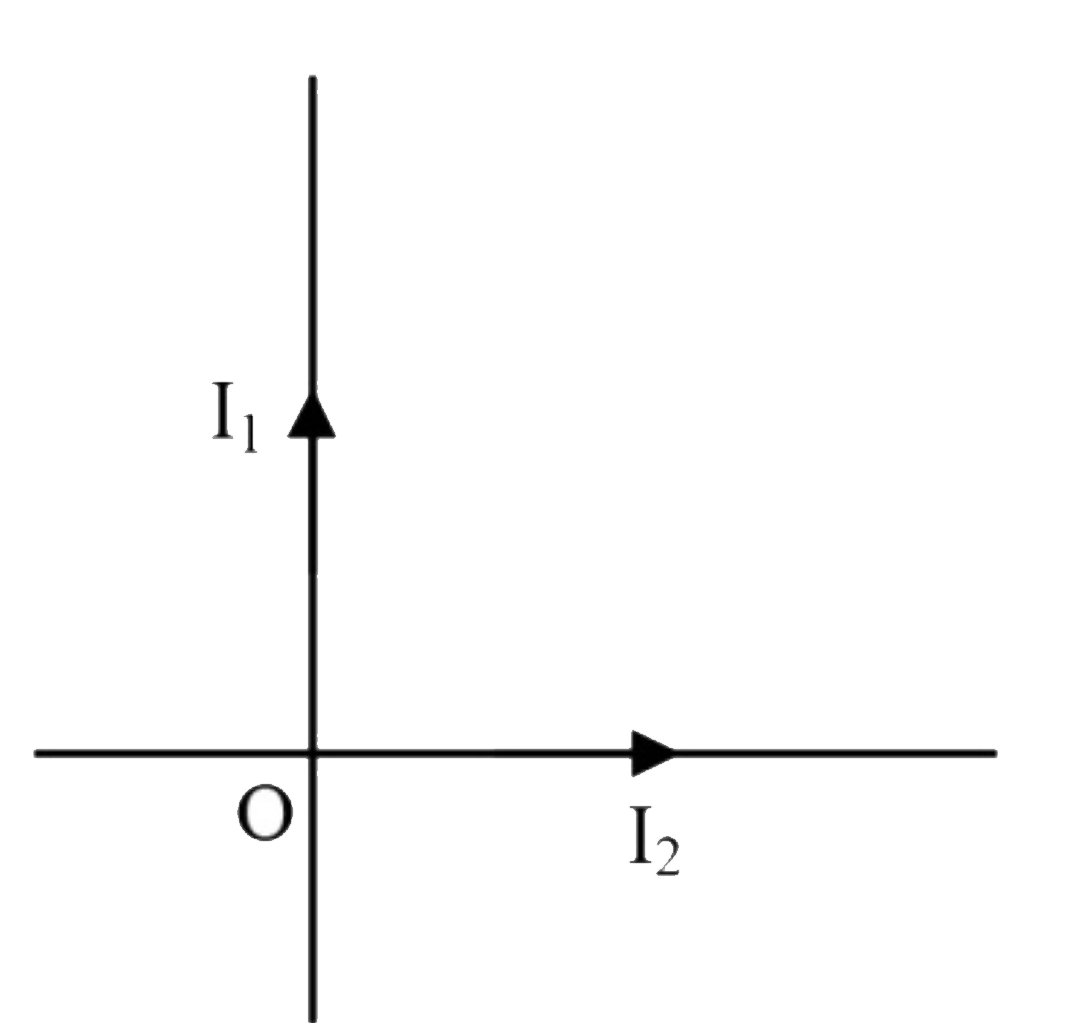
View SolutionTwo long wires carrying current are kept crossed ( not joined at ) . The locus where magnetic field is zero is -
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View SolutionWhen a current carrying coil is placed in a uniform magnetic field with its magnetic moment anti-parallel to the field.
View Solution
