The photoelectric work function for sodium is 2.7 eV. If light of frequency Hz falls on sodium, find (a) the stopping potential, (b)the kinetic energy of the most energetic electrons ejected , and (c ) the speed of those electrons.
Strategy :We will use energy conservation to find the stopping potential. The most energetic electrons will have energy equal to the stopping potential energy .
The stopping potential energy is equal to the photon's energy minus the work function :
The stopping potential is then
The maximum kinetic energy of an electron is then
and the speed of that electron is
m/s
The stopping potential is 1.03 V, the maximum kinetic energy of the electrons that are ejected is 1.03 eV, and the speed of the electrons ejected with maximum kinetic energy is m/s.
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Try Yourself
41 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT SECTION A. Objective (Only one answer)
50 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-J
10 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
Similar Questions
The photoelectric work function of potassium is 3.0 eV. If light having a wavelength of 2475 Å falls on potassium. Find the stopping potential in volts.
View SolutionThe photoelectric work - function of potassium is 2.3 eV. If light
having a wavelength of 2800Å falls on potassium, find
(a) the kinetic energy in electron volts of the most energetic electrons ejected.
(b) the stopping potential in volts.
View SolutionThe work function of a certain metal is 2.3 eV. If light of wave number 2×106m−1 falls on it, the kinetic energies of fastest and slowest ejected electron will be respectively.
View SolutionLight of energy 2.0 eV falls on a metal of work function 1.4 eV . The stopping potential is
View SolutionLight of wavelength 5000Å falls on a sensitive plate with photoelectric work function of 1.9eV. The kinetic energy of the photoelectron emitted will be
View SolutionWhen photon of energy 3.8 eV falls on metallic suface of work function 2.8 eV , then the kinetic energy of emitted electrons are
View SolutionIn photoelectric effect the work function of a metal is 3.5 eV. The emitted electrons can be stopped by applying a potential of –1.2 V. Then
View SolutionFigure is the plot of the stopping potential versus the frequency of the light used in an experiment on photoelectric effect. Find (a) the ratio h/e and (b) the work function.
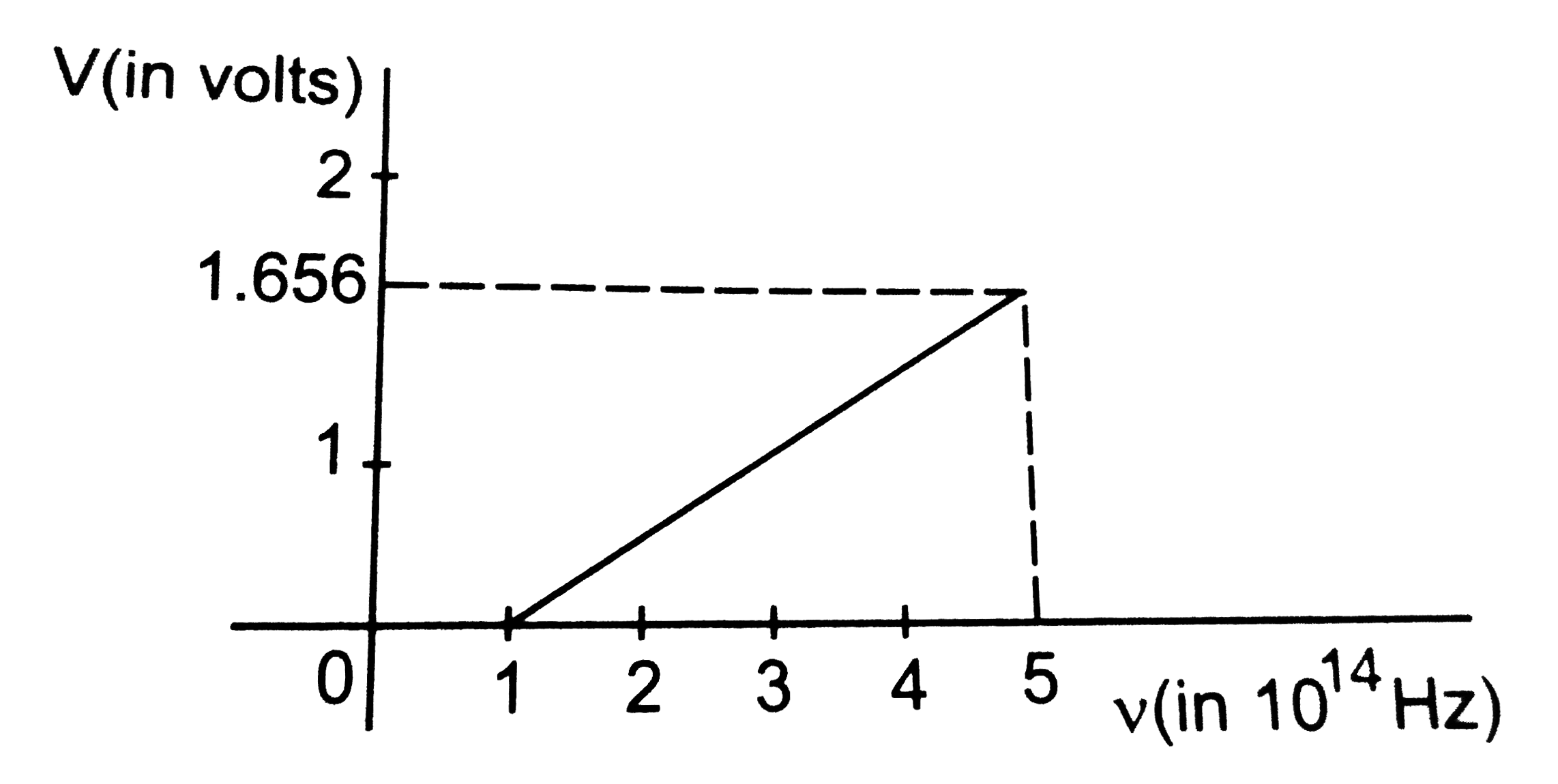
View SolutionLight form a dicharge tube containing hydrogen atoms falls on the surface of a piece of sodium. The kinetic energy of the fastest photoelectrons emitted from sodium is 0.73 eV. The work function for sodium is 1.82 eV. Find (a) the energy of the photons causing the photoelectrons emission.
(b) the quatum numbers of the two levels involved in the emission of these photons.
(c ) the change in the angular momentum of the electron in the hydrogen atom, in the above transition, and
(d) the recoil speed of the emitting atom assuming it to be at rest before the transition. (lonization potential of hydrogen is 13.6 eV.)
View SolutionUltraviolet light of 6.2eV falls on Aluminium surface (work function = 2.2eV). The kinetic energy in joules of the fastest electron emitted is approximately:
View Solution
