A perfectly reflecting solid hemisphere of radius R is placed in the path of a parallel beam of light of large aperture. If the beam carrries an intensity l, find the force exerted by the beam on the hemisphere.
2πR2lc
πR2lc
4πR2lc
πR2l2c
The correct Answer is:2
To find the force exerted by a parallel beam of light on a perfectly reflecting solid hemisphere, we can follow these steps:
1. Understanding the Setup:
- We have a perfectly reflecting solid hemisphere of radius R placed in the path of a parallel beam of light with intensity I.
- The beam of light is large enough to cover the hemisphere.
2. Calculating the Affected Area:
- The area of the flat circular face of the hemisphere that is exposed to the light is given by:
A=πR2
3. Understanding Light Pressure:
- When light strikes a surface, it exerts pressure. For a perfectly reflecting surface, the pressure P exerted by the light can be expressed as:
P=Ic
- Here, I is the intensity of the light, and c is the speed of light.
4. Calculating the Force:
- The force F exerted by the light on the hemisphere can be calculated using the relationship between pressure and force:
F=P⋅A
- Substituting the expressions for pressure and area, we get:
F=(Ic)⋅(πR2)
- Therefore, the force exerted by the beam on the hemisphere is:
F=πR2Ic
Final Answer:
The force exerted by the beam on the hemisphere is:
F=πR2Ic
- We have a perfectly reflecting solid hemisphere of radius R placed in the path of a parallel beam of light with intensity I.
- The beam of light is large enough to cover the hemisphere.
- The area of the flat circular face of the hemisphere that is exposed to the light is given by:
A=πR2
- When light strikes a surface, it exerts pressure. For a perfectly reflecting surface, the pressure P exerted by the light can be expressed as:
P=Ic
- Here, I is the intensity of the light, and c is the speed of light.
- The force F exerted by the light on the hemisphere can be calculated using the relationship between pressure and force:
F=P⋅A
- Substituting the expressions for pressure and area, we get:
F=(Ic)⋅(πR2)
- Therefore, the force exerted by the beam on the hemisphere is:
F=πR2Ic
The force exerted by the beam on the hemisphere is:
F=πR2Ic
Topper's Solved these Questions
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT SECTION B.Objective (Only one answer)
6 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT SECTION C. Objective (More than one answer)
4 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - Try Yourself
41 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-J
10 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
Similar Questions
What is the force exerted by a Light Beam On a Surface ?
View SolutionA concave lens is placed in the path of a uniform parallel of beam of light falling on a screen as shown . Then
_E01_089_Q01.png)
View SolutionA sphere of radius 1.00 cm is placed in the path of a parallel beam of light of large aperture. The intensity of the light is 0.50 W cm−2. If the sphere completely absorbs the radiation falling on it, find the force exerted by the light beam on the sphere.
View SolutionWhen a thin metal plate is placed in the path of one of the interfering beams of light
View SolutionThree particles each of mass m are placed at the three corners of an equilateral triangle of side a. The work which should be done to increase the sides of the triangle to 2a is
View SolutionA parallel beam of light falls on a solid tranparent sphere.
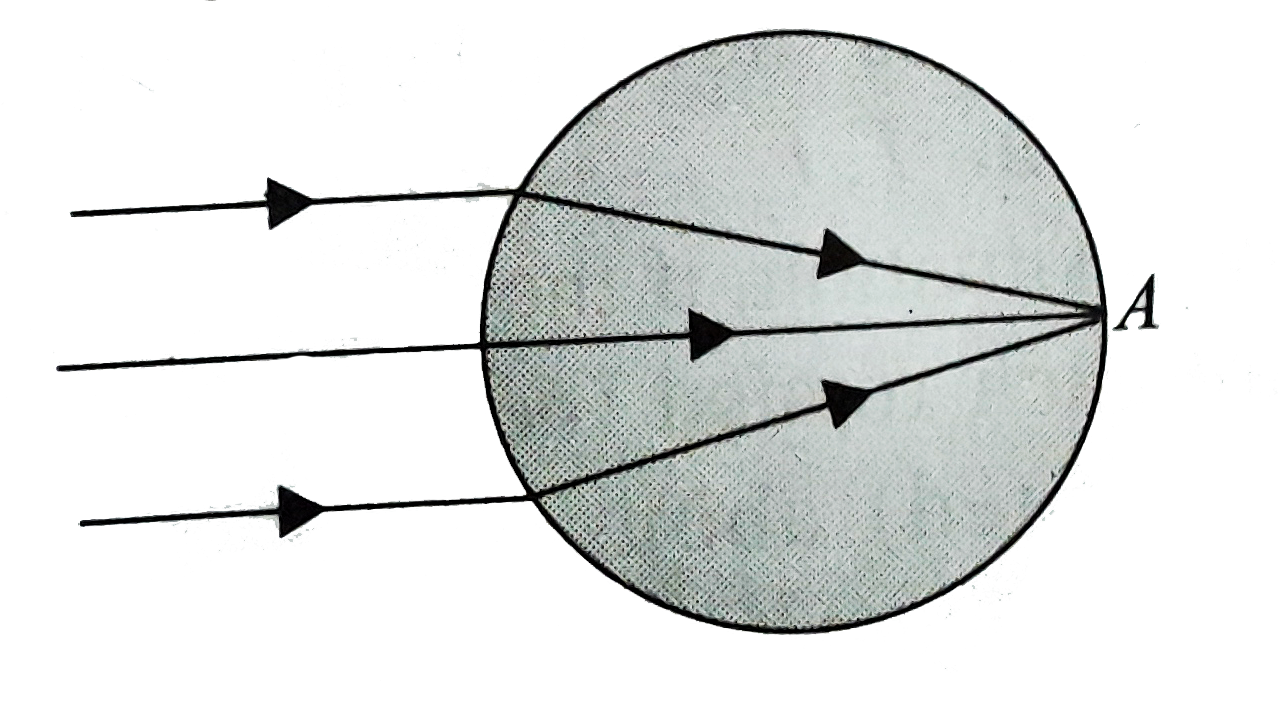
Q. If however thin beam is focussed at A, then find the refractive index of the sphere,
View SolutionA parallel beam of light falls on a solid tranparent sphere.
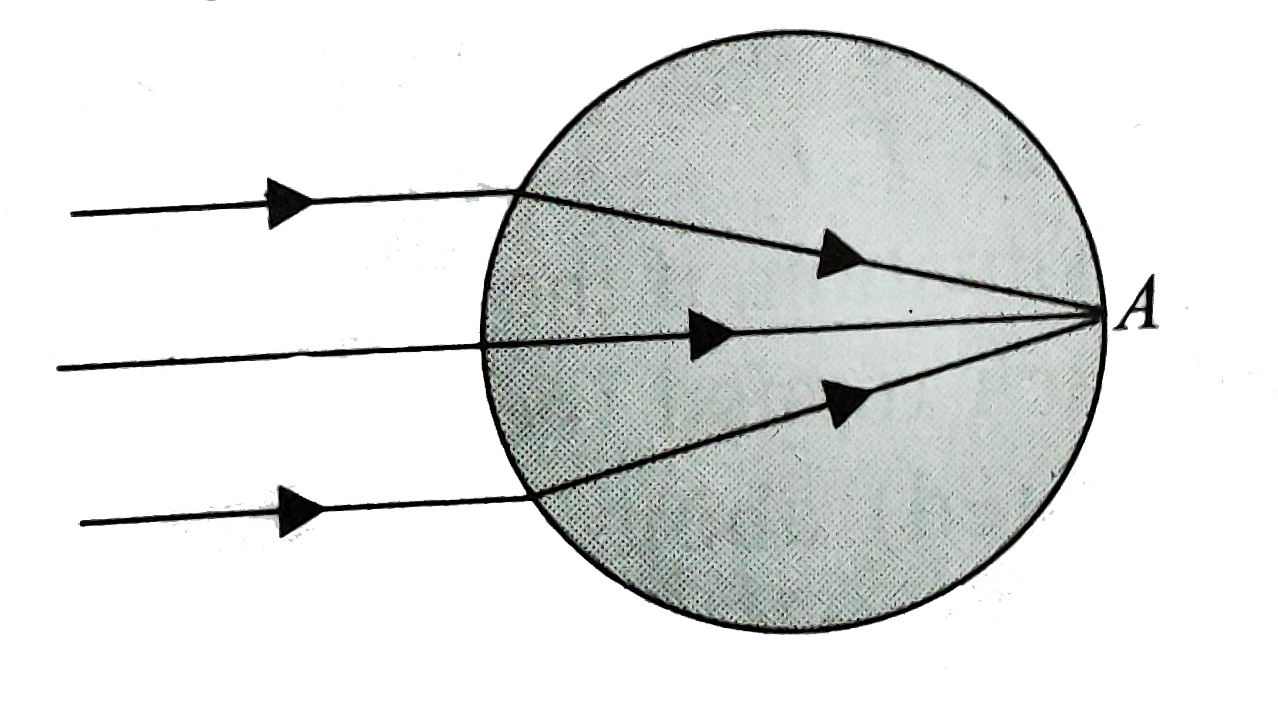
Q. Which is corret?
View SolutionFor an aperture of size a illuminated by a parallel beam of light having wavelength 1, the Fresnel distance is:
View SolutionA beam of white light is incident normally on a plane surface absorbing (70%) of the light and reflecting the rest. If the incident beam carries 10 W of power , find the force exerted by it on the surface .
View SolutionA parellel beam of monochromatic light of wavelength 500 nm is incident normally on a perfectly absorbing surface. The power through any cross section of the beam is 10 W. Find
(a) the number of photons absorbed per second by the surface and
(b) the force exerted by the light beam on the surface.
View Solution
