The following equation gives a relation between the mass m1 kept on a surface of area A and the pressure p exerted on this area.
p=(m1+m2)xA
What must be the dimensions of the quatities x and m2?
To solve the problem, we need to analyze the given equation and determine the dimensions of the quantities x and m2.
1. Understanding the Equation:
The equation given is:
p=(m1+m2)⋅xA
where p is pressure, m1 and m2 are masses, x is a quantity we need to find the dimensions of, and A is the area.
2. Dimensional Formula for Pressure:
The dimensional formula for pressure p is given by:
p=ForceArea=FA
The dimensions of force F are:
(F)=(m)(L)(T−2)=MLT−2
The dimensions of area A are:
(A)=(L2)
Therefore, the dimensions of pressure p become:
(p)=MLT−2L2=ML−1T−2
3. Substituting Dimensions into the Equation:
Now, substituting the dimensions of pressure into the equation:
ML−1T−2=(m1+m2)⋅xA
Since A has dimensions L2, we can rewrite the equation as:
ML−1T−2=(m1+m2)⋅xL2
4. Rearranging the Equation:
Rearranging gives us:
ML−1T−2⋅L2=(m1+m2)⋅x
Simplifying this:
ML1T−2=(m1+m2)⋅x
5. Finding Dimensions of m1+m2:
The dimensions of m1 and m2 are both mass, hence:
(m1)=(m2)=M
Therefore, the dimensions of m1+m2 are:
(m1+m2)=M
6. Finding Dimensions of x:
Now substituting the dimensions of m1+m2 into the equation:
ML1T−2=M⋅x
Dividing both sides by M:
L1T−2=x
Thus, the dimensions of x are:
(x)=LT−2
7. Conclusion:
The dimensions of m2 are:
(m2)=M
The dimensions of x are:
(x)=LT−2
Final Answer:
- Dimensions of m2: M
- Dimensions of x: LT−2
The equation given is:
p=(m1+m2)⋅xA
where p is pressure, m1 and m2 are masses, x is a quantity we need to find the dimensions of, and A is the area.
The dimensional formula for pressure p is given by:
p=ForceArea=FA
The dimensions of force F are:
(F)=(m)(L)(T−2)=MLT−2
The dimensions of area A are:
(A)=(L2)
Therefore, the dimensions of pressure p become:
(p)=MLT−2L2=ML−1T−2
Now, substituting the dimensions of pressure into the equation:
ML−1T−2=(m1+m2)⋅xA
Since A has dimensions L2, we can rewrite the equation as:
ML−1T−2=(m1+m2)⋅xL2
Rearranging gives us:
ML−1T−2⋅L2=(m1+m2)⋅x
Simplifying this:
ML1T−2=(m1+m2)⋅x
The dimensions of m1 and m2 are both mass, hence:
(m1)=(m2)=M
Therefore, the dimensions of m1+m2 are:
(m1+m2)=M
Now substituting the dimensions of m1+m2 into the equation:
ML1T−2=M⋅x
Dividing both sides by M:
L1T−2=x
Thus, the dimensions of x are:
(x)=LT−2
The dimensions of m2 are:
(m2)=M
The dimensions of x are:
(x)=LT−2
- Dimensions of m2: M
- Dimensions of x: LT−2
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - Try Yourself82videos
UNITS AND MEASUREMENTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION A Objective (One option is correct )50videos
UNITS AND MEASUREMENTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)10videos
THERMODYNAMICS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))1videos
WAVE OPTICS
Similar Questions
If system is in equilibrium then find relation between m1 and m2
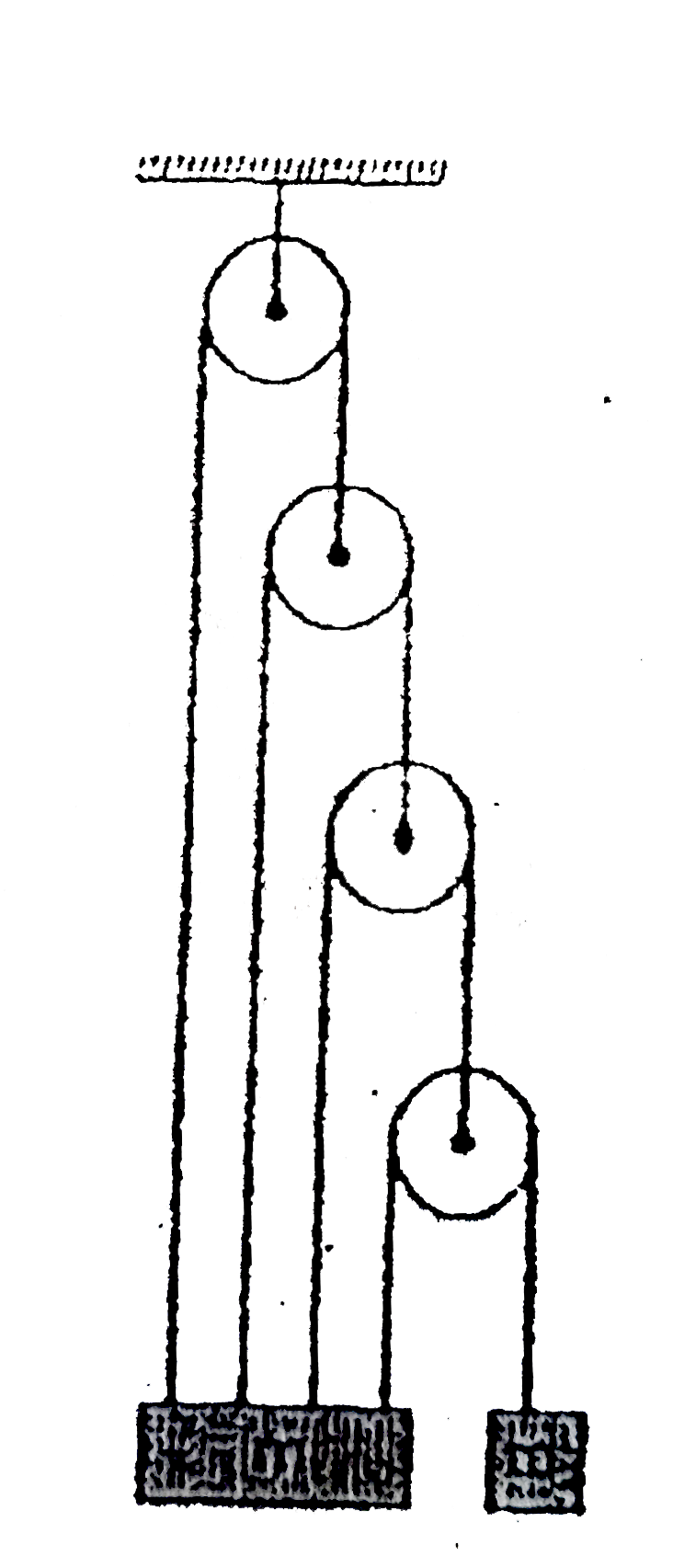 View Solution
View SolutionWhen force F applied on m1 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is on relative motion between m1andm2
 View Solution
View SolutionConsider the system of masses and pulleys shown in fig. with massless string and fricitionless pulleys.
(a) Give the necessary relation between masses m1 and m2 such that system is in equilibrium and does not move.
(b) If m1=6kg and m2=8kg, calculate the magnitude and direction of the acceleration of m1.
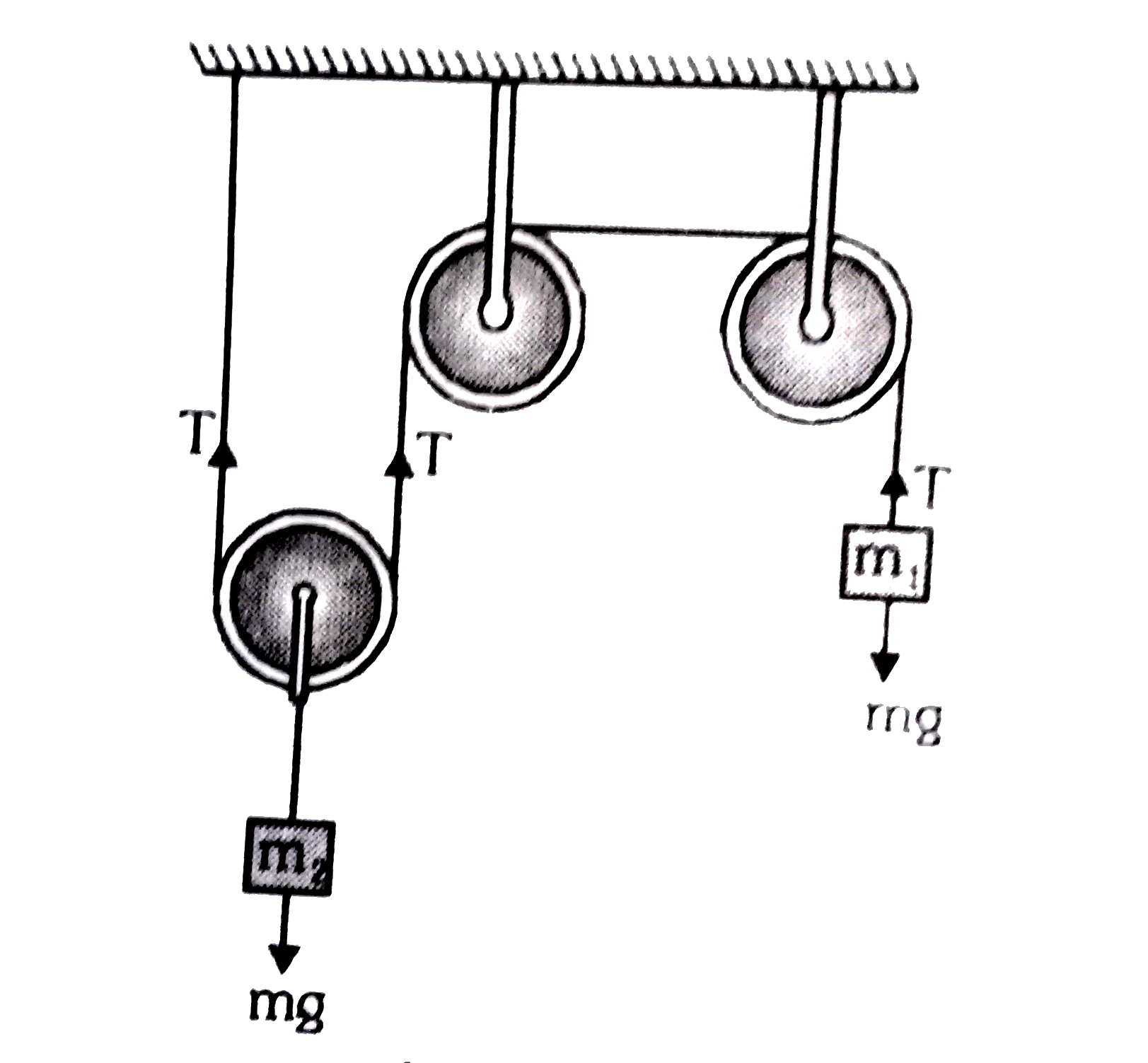 View Solution
View SolutionThe dimensions of a cuboid are in the ratio 5:3:1 and its total surface area is 414 m2. Find the dimensions.
View SolutionWhen a force of one ________ acts on an area of cross-section 1m2, the pressure exerted is said to be one ___________
View SolutionAssertion : Mass of solid floating in liquid is m1 and mass of liquid is m2. Base area is A. Then pressure at bottom is p0+(m1+m2)gA
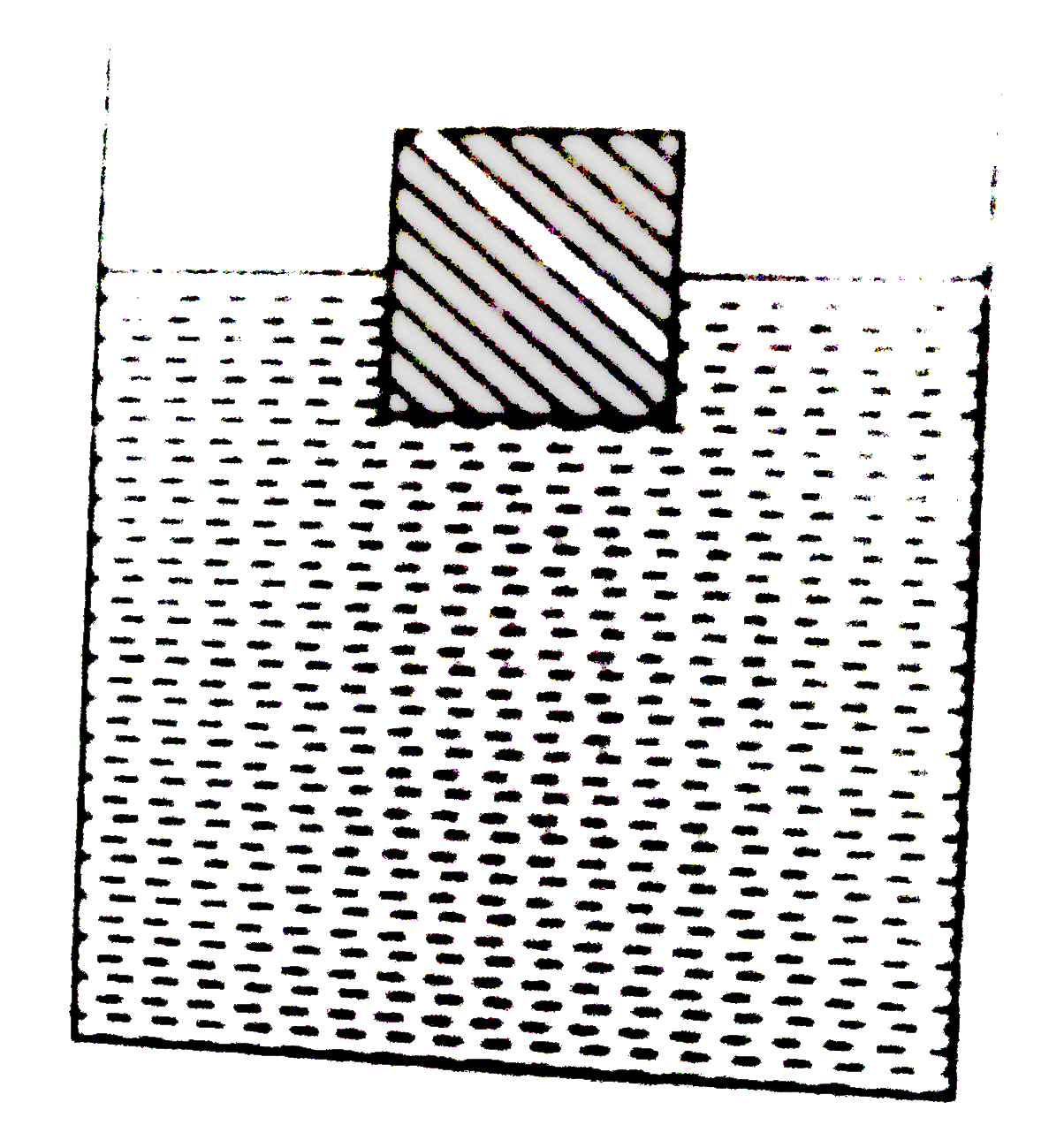
Reason : Upward force on liquid from base of vessel is pA, where p is pressure at bottom.View SolutionThe dimensions of a cuboid are in the ratio of 1:2:3: and its total surface area is 88m2. Find the dimensions.
View SolutionThe dimensions of a cuboid are in the ratio of 1:2:3: and its total surface area is 88m2. Find the dimensions.
View SolutionWhat is the area of cross-section of a body in m2, when it exerts a force of 50 N and produces a pressure of 2000 Pa?
View SolutionA cuboid has total surface area of 40m2 and its lateral surface area is 26m2 . Find the area of its base.
View Solution

