Frequency of sound that can be produced by a pipe depends on length (l) of the pipe, atmospheric pressure (p) and density (d) of air, according to relation v=pbdcta . Find the value of (a +b + c).
The correct Answer is:1
To solve the problem, we need to analyze the given relation for frequency v in terms of atmospheric pressure p, density d, and length l of the pipe. The relation is given as:
v=pbdcla
We need to find the value of a+b+c.
Step 1: Identify the dimensions of each variable
1. Pressure (p): The dimension of pressure is given by force per unit area.
- Force has the dimension (MLT−2) (mass times acceleration).
- Area has the dimension (L2).
- Therefore, the dimension of pressure is:
(p)=(MLT−2)(L2)=(ML−1T−2)
2. Density (d): The dimension of density is mass per unit volume.
- Volume has the dimension (L3).
- Therefore, the dimension of density is:
(d)=(M)(L3)=(ML−3)
3. Length (l): The dimension of length is simply:
(l)=(L)
4. Frequency (v): The dimension of frequency is the inverse of time.
(v)=(T−1)
Step 2: Substitute the dimensions into the equation
Substituting the dimensions into the equation v=pbdcla:
(T−1)=((ML−1T−2))b⋅((ML−3))c((L))a
Step 3: Expand the right-hand side
Expanding the right-hand side gives:
(T−1)=(MbL−bT−2b)⋅(McL−3c)(La)
Combining the terms:
(T−1)=(Mb+cL−b−3cT−2b)(La)=(Mb+cL−b−3c−aT−2b)
Step 4: Equate the dimensions
Now we equate the dimensions on both sides:
1. For mass M:
b+c=0(1)
2. For length L:
−b−3c−a=0(2)
3. For time T:
−2b=−1⇒2b=1⇒b=12(3)
Step 5: Solve for c and a
Substituting b=12 into equation (1):
12+c=0⇒c=−12(4)
Now substituting b=12 and c=−12 into equation (2):
−12−3(−12)−a=0
This simplifies to:
−12+32−a=0⇒2−a=0⇒a=1(5)
Step 6: Calculate a+b+c
Now we can find a+b+c:
a+b+c=1+12−12=1
Final Answer
Thus, the value of a+b+c is:
1
1. Pressure (p): The dimension of pressure is given by force per unit area.
- Force has the dimension (MLT−2) (mass times acceleration).
- Area has the dimension (L2).
- Therefore, the dimension of pressure is:
(p)=(MLT−2)(L2)=(ML−1T−2)
- Volume has the dimension (L3).
- Therefore, the dimension of density is:
(d)=(M)(L3)=(ML−3)
(l)=(L)
(v)=(T−1)
Substituting the dimensions into the equation v=pbdcla:
Expanding the right-hand side gives:
Now we equate the dimensions on both sides:
b+c=0(1)
−b−3c−a=0(2)
−2b=−1⇒2b=1⇒b=12(3)
Substituting b=12 into equation (1):
Now we can find a+b+c:
Thus, the value of a+b+c is:
Topper's Solved these Questions
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION H (Multiple True-False)
6 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION I (Subjective)
18 Videos
- UNITS AND MEASUREMENTSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - UNITS AND MEASUREMENTSEXERCISE - ASSIGNMENT SECTION F (Matrix-Match)
6 Videos
- THERMODYNAMICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THERMODYNAMICSEXERCISE - ASSIGNMENT (SECTION -D) (Assertion - Reason Type Questions)
10 Videos
- WAVE OPTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - WAVE OPTICSEXERCISE - Assignment (Section-J (Aakash Challengers question))
1 Videos
Similar Questions
The velocity v of the a particle depends upen the time t according to the equation v=a+bt+cd+1 Write the dimension of a, b,c and d.
View SolutionA gas bubble from an explosion under water oscillates with a period T proportional to padbEcwhere p is the static pressure d is the density of water and E is the total energy of explosion. Find the value of a,b and c.
View Solution
Knowledge Check
Ratio of CP and Cv depends upon temperature according to the following relation
Aγα TBγα1/TCγα√TDγαTo
If a,b,c,d,e are in A.P., the find the value of a−4b+6c−4d+e.
View SolutionA vertical pipe open at both ends is partially submerged in water . A tuning fork is unknown frequency is placed near the top of the pipe and made to vibrate . The pipe can be moved up and down and thus length of air column the pipe can be adjusted. For definite lengths of air column in the pipe, standing waves will be set up as a result of superposition of sound waves travelling in opposite directions. Smallest value of length of air column , for which sound intensity is maximum is 10cm[ take speed of sound , v=344m/s].
Answer the following questions.
Length of air column for third resonance will be
View SolutionA vertical pipe open at both ends is partially submerged in water . A tuning fork is unknown frequency is placed near the top of the pipe and made to vibrate . The pipe can be moved up and down and thus length of air column the pipe can be adjusted. For definite lengths of air column in the pipe, standing waves will be set up as a result of superposition of sound waves travelling in opposite directions. Smallest value of length of air column , for which sound intensity is maximum is 10cm[ take speed of sound , v=344m/s].
Answer the following questions.
Frequency of the tuning fork is
View SolutionA vertical pipe open at both ends is partially submerged in water . A tuning fork is unknown frequency is placed near the top of the pipe and made to vibrate . The pipe can be moved up and down and thus length of air column the pipe can be adjusted. For definite lengths of air column in the pipe, standing waves will be set up as a result of superposition of sound waves traveling in opposite directions. Smallest value of length of air column , for which sound intensity is maximum is 10cm [ take speed of sound , v=344m/s].
Answer the following questions.
The air column here is closed at one end because the surface of water acts as a wall. Which of the following is correct ?
View SolutionA storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -
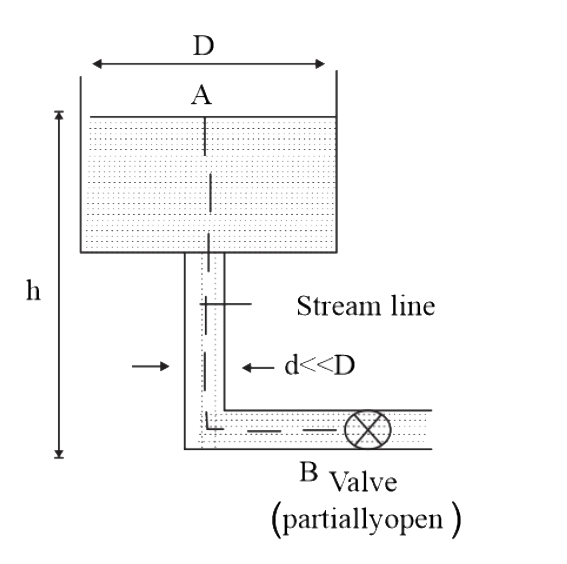
View SolutionIf a,b,c,andd are in H.P., then find the value of a−2−d−2b−2−c−2 .
View SolutionTwo narrow cylindrical pipes AandB have the same length. Pipe A is open at both ends and is filled with a monoatomic gas of molar mass MA. Pipe B is open at one end and closed at the other end, and is filled with a diatomic gas of molar mass MB. Both gases are at the same temperature.
(a) If the frequency of the second harmonic of the fundamental mode in pipe A is equal to the frequency of the third harmonic of the fundamental mode in pipe B, determine the value of MB/MB.
(b) Now the open end of pipe B is also closed (so that the pipe is closed at both ends). Find the ratio of the fundamental frequency in pipe A to that in pipe B.
View Solution
