Choose the proposition among the following that is true for all
(a)
(b)
(c)
(d)
The correct Answer is:C
To solve the problem, we need to evaluate the sum of the series given in the question and compare it with the provided options to determine which proposition is true for all natural numbers n.
1. Understanding the Series: We need to evaluate the sum:
Sn=n∑r=1tan−1(1r2+r+1)
2. Simplifying the General Term: The general term can be rewritten as:
tan−1(1r2+r+1)=tan−1(11+r(r+1))
We can express 1 in the numerator as (r+1)−r:
=tan−1((r+1)−r1+r(r+1))
3. Using the Tan Inverse Identity: We apply the identity:
tan−1(a)−tan−1(b)=tan−1(a−b1+ab)
This gives us:
tan−1(r+1)−tan−1(r)
4. Rewriting the Sum: Thus, we can rewrite the sum Sn:
Sn=n∑r=1(tan−1(r+1)−tan−1(r))
5. Telescoping Series: This is a telescoping series, where most terms cancel out:
Sn=tan−1(n+1)−tan−1(1)
6. Calculating the Result: Since tan−1(1)=π4, we have:
Sn=tan−1(n+1)−π4
7. Final Expression: We can express this as:
Sn=tan−1(n+1−11+(n+1)⋅1)=tan−1(nn+2)
8. Comparing with Options: Now we compare Sn with the given options:
- Option A: tan−1(3n−13n+3)
- Option B: tan−1(3n−14n+2)
- Option C: tan−1(nn+2)
- Option D: tan−1(2n−13n)
We find that:
Sn=tan−1(nn+2)
matches with Option C.
Conclusion
Thus, the correct answer is Option C: tan−1(nn+2).
Sn=n∑r=1tan−1(1r2+r+1)
tan−1(1r2+r+1)=tan−1(11+r(r+1))
We can express 1 in the numerator as (r+1)−r:
=tan−1((r+1)−r1+r(r+1))
tan−1(a)−tan−1(b)=tan−1(a−b1+ab)
This gives us:
tan−1(r+1)−tan−1(r)
Sn=n∑r=1(tan−1(r+1)−tan−1(r))
Sn=tan−1(n+1)−tan−1(1)
Sn=tan−1(n+1)−π4
Sn=tan−1(n+1−11+(n+1)⋅1)=tan−1(nn+2)
- Option A: tan−1(3n−13n+3)
- Option B: tan−1(3n−14n+2)
- Option C: tan−1(nn+2)
- Option D: tan−1(2n−13n)
Sn=tan−1(nn+2)
matches with Option C.
Thus, the correct answer is Option C: tan−1(nn+2).
Topper's Solved these Questions
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-C(Linked Comprehension Type Questions)
6 Videos
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)
11 Videos
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Assignmenet ((Section-A(Objective Type Questions (One option is correct))
11 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section-J (Aakash Challengers Questions)
7 Videos
- PROBABILITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PROBABILITYEXERCISE - ASSIGNMENT SECTION-J (aakash challengers questions)
11 Videos
Similar Questions
Knowledge Check
Choose the correct option among the following.
 Aii,I,iii,ivBiv,I,iii,iiCI,ii,iii,ivDI,iv,ii,iii
Aii,I,iii,ivBiv,I,iii,iiCI,ii,iii,ivDI,iv,ii,iiiChoose the correct among the following statements :
A B
B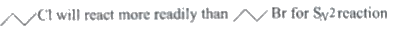 C
C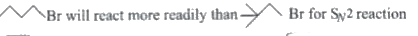 D
D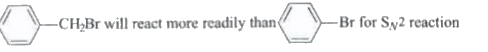
Choose the correct option among the following

View SolutionWhich among the following is true ?
View SolutionChoose the strongest base among the following :
View SolutionChoose the strongest base among the following:
View SolutionChoose the coorect statement among the following:
View SolutionChoose the correct statement among the following
View Solution
