STATEMENT-1 : The differential equation of all circles in a plane can be of order 3.
and
STATEMENT-2 : General equation of a circle in plane has three independent constant parameters
Statement-1 is true, Statement-2 is true, Statement-2 is a correct explanation for Statement-1.
Statement-1 is true, Statement-2 is true, Statement-2 is NOT a correct explanation for Statement-1.
Statement-1 is True, Statement-2 is False
Statement-1 is False, Statement-2 is True
The correct Answer is:A
To solve the problem, we need to analyze both statements regarding circles in a plane and their differential equations.
Step 1: Write the General Equation of a Circle
The general equation of a circle in a plane is given by:
x2+y2+2gx+2fy+c=0
where g, f, and c are constants.
Step 2: Identify the Parameters
From the general equation, we can see that there are three independent constant parameters:
- g (related to the x-coordinate of the center)
- f (related to the y-coordinate of the center)
- c (related to the radius of the circle)
Step 3: Differentiate the Equation
To find the differential equation that represents all circles, we need to differentiate the general equation. Since we have three parameters, we will differentiate the equation three times to eliminate these parameters.
1. First Derivative:
ddx(x2+y2+2gx+2fy+c)=0
This gives us:
2x+2ydydx+2g+2fdydx=0
2. Second Derivative:
We differentiate the first derivative again to eliminate g and f:
ddx(2x+2ydydx+2g+2fdydx)=0
3. Third Derivative:
We differentiate the second derivative to eliminate the last parameter:
ddx(Second Derivative)=0
Step 4: Order of the Differential Equation
After differentiating three times, we will arrive at a differential equation that does not contain any of the parameters g, f, or c. Thus, the order of the differential equation representing all circles in a plane is 3.
Conclusion
- Statement 1: The differential equation of all circles in a plane can be of order 3. (True)
- Statement 2: The general equation of a circle in a plane has three independent constant parameters. (True)
Since both statements are true, and Statement 2 correctly explains Statement 1, we conclude that both statements are valid.
---
The general equation of a circle in a plane is given by:
x2+y2+2gx+2fy+c=0
where g, f, and c are constants.
From the general equation, we can see that there are three independent constant parameters:
- g (related to the x-coordinate of the center)
- f (related to the y-coordinate of the center)
- c (related to the radius of the circle)
To find the differential equation that represents all circles, we need to differentiate the general equation. Since we have three parameters, we will differentiate the equation three times to eliminate these parameters.
ddx(x2+y2+2gx+2fy+c)=0
This gives us:
2x+2ydydx+2g+2fdydx=0
We differentiate the first derivative again to eliminate g and f:
ddx(2x+2ydydx+2g+2fdydx)=0
We differentiate the second derivative to eliminate the last parameter:
ddx(Second Derivative)=0
After differentiating three times, we will arrive at a differential equation that does not contain any of the parameters g, f, or c. Thus, the order of the differential equation representing all circles in a plane is 3.
- Statement 1: The differential equation of all circles in a plane can be of order 3. (True)
- Statement 2: The general equation of a circle in a plane has three independent constant parameters. (True)
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Assignment Section - F (Matrix-Match Type Questions)2videos
DIFFERENTIAL EQUATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Assignment Section-G (Integer Answer Type Questions)3videos
DIFFERENTIAL EQUATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DIFFERENTIAL EQUATIONSEXERCISE - Assignment Section - D (Linked Comprehension Type Questions))11videos
DIFFERENTIAL EQUATIONS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DETERMINANTS EXERCISE - SECTION - J12videos
DETERMINANTS
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - INTEGRALSEXERCISE - Try yourself50videos
INTEGRALS
Similar Questions
Match the following
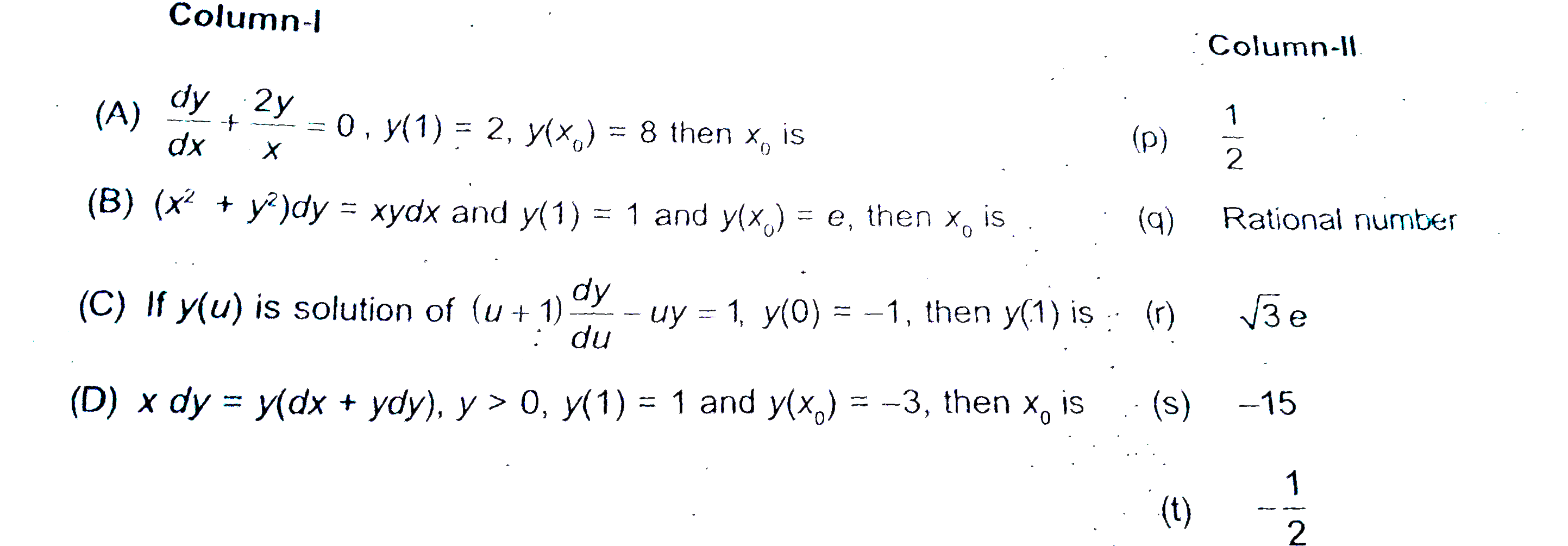 02:57View Solution
02:57View SolutionIf xsin(yx)dy=(ysin(yx)−x)dxand y(1) =π2 then the value of cos(ye7) is __________.
06:02View SolutionNewton's law of cooling states that the rate of change of the temperature T of an object is proportional to the difference between T and the (constant) temperature τ of the surrounding medium, we can write it as dTdt=−k(T−τ)k>0 constant
An cup of coffee is served at 185∘F in a room where the temperature is 65∘F. 2 minutes later the temperature of the coffee has dropped to 155∘F.
loge3=1.09872,loge.34=0.2877
Temperature of coffee at time t is given by01:28View SolutionIn the determinant ∣∣ ∣∣01−2−1032−30∣∣ ∣∣, value of co-factor to its minor element of -3 is
03:43View SolutionFind an anti-derivative of sec2(x4).
05:41View SolutionStatement 1 : The differential equation of all circles in a plane must be of order 3. Statement 2 : There is only one circle passing through three non-collinear points.
01:24View SolutionSTATEMENT-1 : To find complete solution of a second order differential equation we need two different conditions.
and
STATEMENT-2 : An nth order differential equation has n independent parameters.02:59View SolutionSTATEMENT-1 : The differential equation of all non-horizontal lines in a plane d2ydx2=0
and
STATEMENT-2 : The general equation of all non-horizontal line in xy plane is ax + by = 1, a≠001:53View SolutionSTATEMENT-1 : The differential equation of all circles in a plane can be of order 3.
and
STATEMENT-2 : General equation of a circle in plane has three independent constant parameters03:10View Solutionx-y तल में स्थित समस्त वृत्तों का अवकल समीकरण ज्ञात कीजिये।
11:22View SolutionThe general solution of the differential equation of all circles having centre at A(-1, 2) is ..... .
04:39View Solutionनिम्नलिखित कथनो पर विचार कीजिए
I. एक ही तल में स्थित सभी वृत्तों की अवकल समीकरण की कोटि है।
II. यदि तीन असंरेखीय बिन्दु है, तब उनसे होकर केवल एक वृत्त खींचा जा सकता है।
उपरोक्त कथनो में से कौन-सा/से कथन सही है/है?01:18View SolutionStatement 1 : The differential equation of all circles in a plane must be of order 3.
Statement 2 : There is only one circle passing through three non-collinear points.04:51View SolutionStatement I The order of the differential equation representing all the circles in a plane is 3. Statement II If three points in a plane are nonlinear, then always more than one circle passes through these points.
01:30View Solutionxy, समतल में r त्रिज्या के सभी वृतों के निकाय का अवकल समीकरण है
01:55View Solution

