Statement-1 :If a≤xi≤b where xi denotes the value of x in the ith case for i=1,2,….n, then (b−a)2≤ Variance (x) .
Statement-2 : S.D. ≤ range (b-a)
The correct Answer is:3
To solve the problem, we need to analyze the two statements given in the question regarding variance and standard deviation.
Step 1: Understand the Given Statements
We have two statements:
- Statement 1: If a≤xi≤b for i=1,2,…,n, then (b−a)2≤Variance(x).
- Statement 2: Standard Deviation ≤ Range (b−a).
Step 2: Analyze Statement 1
1. Definition of Variance: The variance of a set of values x1,x2,…,xn is defined as:
Variance(x)=1nn∑i=1(xi−¯x)2
where ¯x is the mean of the values.
2. Range: The range of the data is defined as b−a.
3. Mean Location: Since a≤xi≤b, the mean ¯x must also lie between a and b. Thus, the deviations (xi−¯x) will also be bounded.
4. Bounding the Variance: The maximum deviation from the mean ¯x can be at most b−a. Therefore:
(xi−¯x)2≤(b−a)2
for all i.
5. Summing Deviations: When we sum these squared deviations:
n∑i=1(xi−¯x)2≤n(b−a)2
Dividing by n gives:
Variance(x)≤(b−a)2n⋅n=(b−a)2
This contradicts Statement 1, which claims (b−a)2≤Variance(x). Thus, Statement 1 is incorrect.
Step 3: Analyze Statement 2
1. Standard Deviation: The standard deviation σ is the square root of the variance:
σ=√Variance(x)
2. Using the Result from Statement 1: Since we found that Variance(x)≤(b−a)2, we can take the square root:
σ≤√(b−a)2=|b−a|=b−a
Therefore, Statement 2 is correct.
Conclusion
- Statement 1: Incorrect
- Statement 2: Correct
We have two statements:
- Statement 1: If a≤xi≤b for i=1,2,…,n, then (b−a)2≤Variance(x).
- Statement 2: Standard Deviation ≤ Range (b−a).
1. Definition of Variance: The variance of a set of values x1,x2,…,xn is defined as:
Variance(x)=1nn∑i=1(xi−¯x)2
where ¯x is the mean of the values.
(xi−¯x)2≤(b−a)2
for all i.
n∑i=1(xi−¯x)2≤n(b−a)2
Dividing by n gives:
Variance(x)≤(b−a)2n⋅n=(b−a)2
This contradicts Statement 1, which claims (b−a)2≤Variance(x). Thus, Statement 1 is incorrect.
1. Standard Deviation: The standard deviation σ is the square root of the variance:
σ=√Variance(x)
σ≤√(b−a)2=|b−a|=b−a
Therefore, Statement 2 is correct.
- Statement 1: Incorrect
- Statement 2: Correct
Topper's Solved these Questions
- STATISTICSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STATISTICSEXERCISE - Section-B Linked Comprehension
5 Videos
- SETS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SETS EXERCISE - SECTION-I(Aakash Challengers Questions)
4 Videos
- STRAIGHT LINESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
5 Videos
Similar Questions
Knowledge Check
If 02≤x≤2, the maximum value of f(x)=1−x2 is
A2B1C0D−1If 2≤2x−3≤5,x∈I, then the solution set of x on the number line is:
A B
B C
C D
D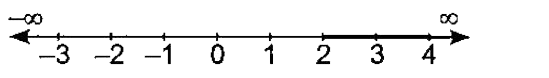
If 2x−3≤x+1≤4x+7,x∈I (integers), then the solution set of x is
A{−2,−1,0,1,2,3,4}B{−1,0,1,2,3}C{−2,−1,0,1,2,3}D{−1,0,1,2,3,4}
Find the values of x which satisfy the inequation: −2≤12−2x≤156,xεN
View SolutionThe range of x for which 2≤|x−1|≤3.
View SolutionLet A denotes the set of values of x for which x+2x−4≤0 and B denotes the set of values of x for which x2−ax−4≤0. If B is the subset of A then a cannot take integral value (a) 0, (b) 1 (c) 2 (d) 3
View SolutionLet A denotes the set of values of x for which x+2x−4≤0 and B denotes the set of values of x for which x2−ax−4≤0. If B is the subset of A then a cannot take integral value (a) 0, (b) 1 (c) 2 (d) 3
View SolutionUse real number line to find the range of values of x for which :
−1<x≤6and−2≤x≤3.
View Solution
