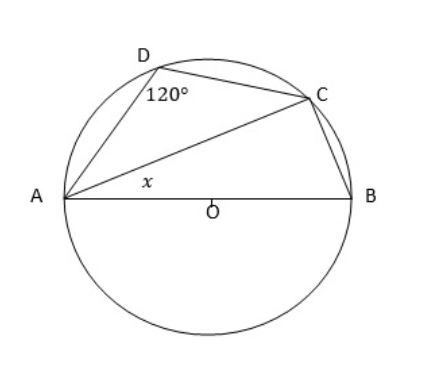
The number of different circles passing through the points A,B,C,D,E,F and G as shown in the adjacent figure.
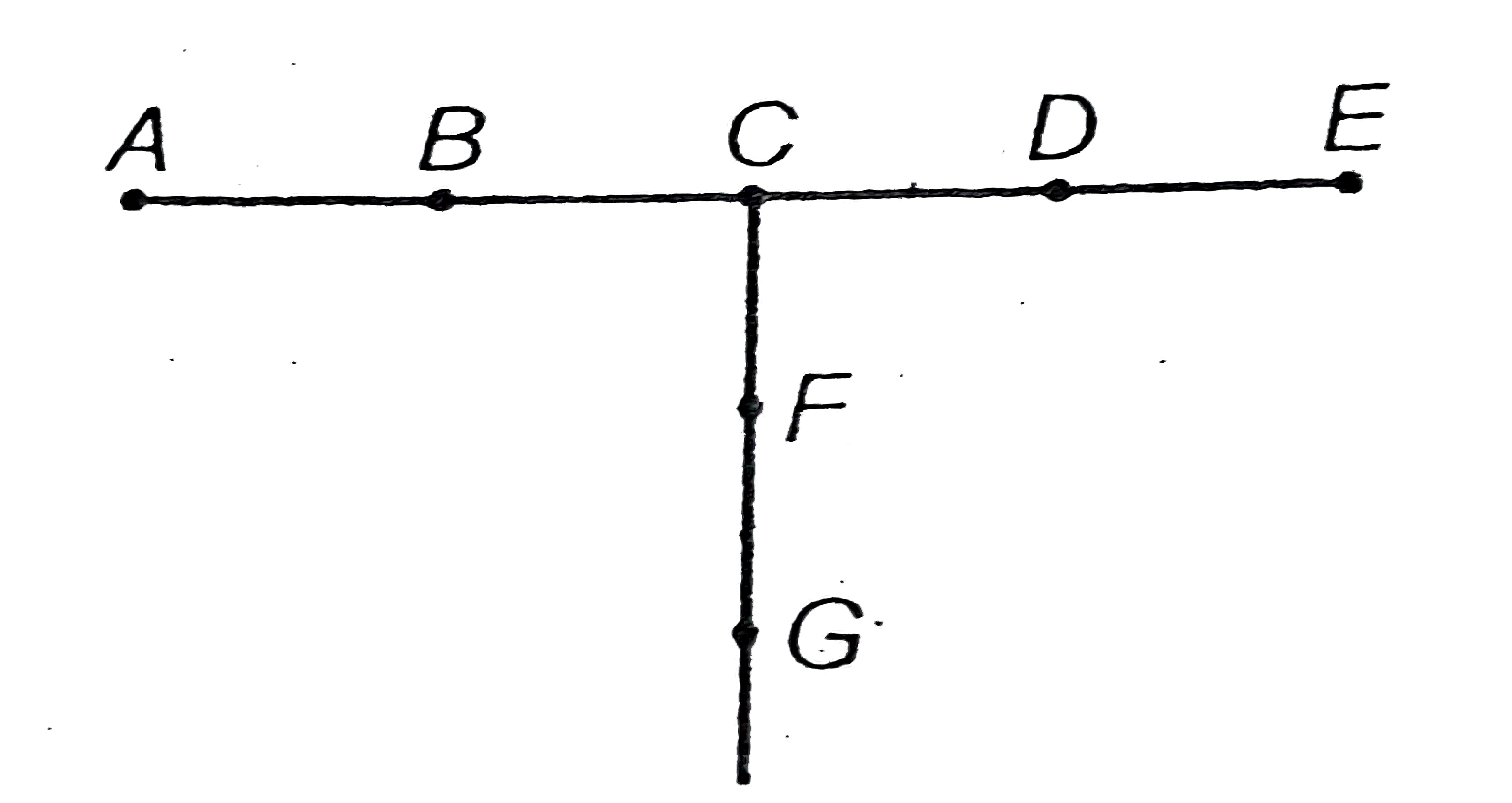
We know that from three non-collinear points one and only one circle can be drawn.
Hence, the number of different circles.
=Number of 3 non-collinear points selected from the given figure
=5C2×2C1+4C1×2C2
=20+4=24
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Try Yourself
65 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section A Objective type questions (One option is correct )
51 Videos
- MATRICESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATRICESEXERCISE - Assignment (Section - J) Aakash Challengers Questions
3 Videos
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)
11 Videos
Similar Questions
Knowledge Check
The five number 1056, 1098, 1100 and 1126 are represented on a number line by the point A, B, C, D and E, respectively, as shown in the figure. Which one of the following points represents the average of the five numbers ?
 APoint ABPoint BCPoint CDPoint D
APoint ABPoint BCPoint CDPoint DThe path of reflex arc is shown in the given figure.Identify the different labellings A,B,C,D,E,F and select the correct option.
 AABCDEFStimulusEffectorSensory nerveMotor nerveReceptorResponseBABCDEFStimulusReceptorSensory nerveMotor nerveEffectorResponseCABCDEFStimulusEffectorMotor nerveSensory nerveReceptorResponseDABCDEFStimulusReceptorMotor nerveSensory nerveEffectorResponse
AABCDEFStimulusEffectorSensory nerveMotor nerveReceptorResponseBABCDEFStimulusReceptorSensory nerveMotor nerveEffectorResponseCABCDEFStimulusEffectorMotor nerveSensory nerveReceptorResponseDABCDEFStimulusReceptorMotor nerveSensory nerveEffectorResponse
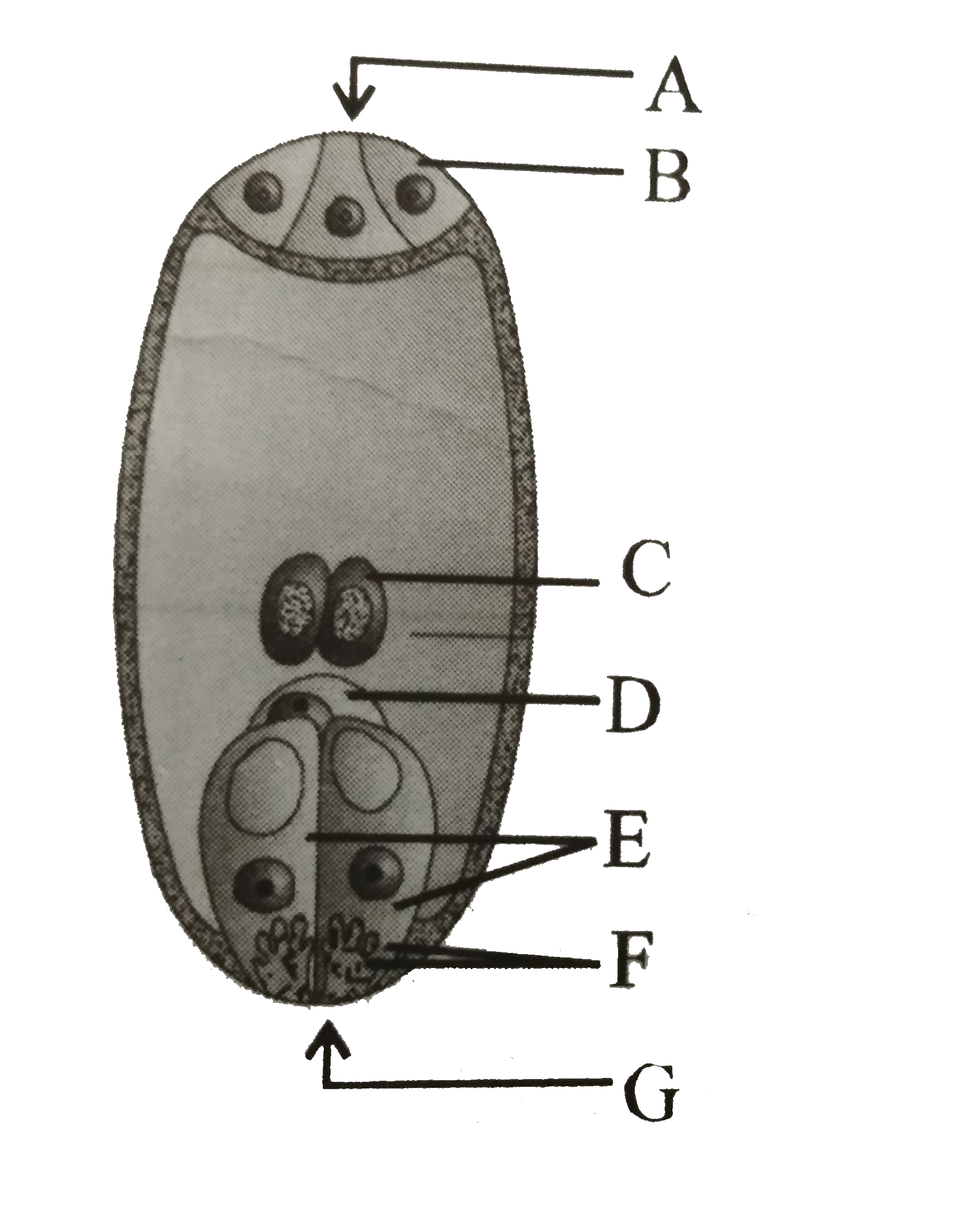
Identify A, B, C, D, E, F,G
View SolutionThere are 10 points in a plane of which no three points are collinear and four points are concyclic. The number of different circles that can be drawn through at least three points of these points is (A) 116 (B) 120 (C) 117 (D) none of these
View SolutionThere are five points A,B,C,D and E. no three points are collinear and no four are concyclic. If the line AB intersects of the circles drawn through the five points. The number of points of intersection on the line apart from A and B is
View SolutionIn Figure, ABCD is a cyclic quadrilateral. A circle passing through A and B meets AD and BC in the points E and F respectively. Prove that EF∣∣DC
View SolutionNumber of circles that can be drawn through three non-collinear points is (a) 1 (b) 0 (c) 2 (d) 3
View SolutionIn the adjacent figure a parabola is drawn to pass through the vertices B,C and D of the square ABCD. If A(2,1),C(2,3), then focus of this parabola is

View Solution