IN a meeting everyone had shaken hands with everyone else, it was found that 66 handshakes were exchanged . Number of persons present in the meeting is
17
12
13
18
The correct Answer is:B
To solve the problem of finding the number of persons present in a meeting where 66 handshakes were exchanged, we can follow these steps:
1. Understanding the Problem:
We know that in a meeting, every person shakes hands with every other person. The total number of handshakes is given as 66.
2. Setting Up the Equation:
Let the total number of persons in the meeting be denoted by n. The number of ways to choose 2 persons from n persons (which represents one handshake) is given by the combination formula (n2). This can be expressed as:
(n2)=n(n−1)2
According to the problem, this is equal to 66:
n(n−1)2=66
3. Eliminating the Fraction:
To eliminate the fraction, multiply both sides of the equation by 2:
n(n−1)=132
4. Rearranging the Equation:
Rearranging gives us a quadratic equation:
n2−n−132=0
5. Factoring the Quadratic:
We need to factor the quadratic equation. We look for two numbers that multiply to -132 and add to -1. The numbers are -12 and 11. Thus, we can factor the equation as:
(n−12)(n+11)=0
6. Finding the Roots:
Setting each factor to zero gives us:
n−12=0orn+11=0
This results in:
n=12orn=−11
7. Interpreting the Results:
Since n represents the number of persons, it cannot be negative. Therefore, we discard n=−11.
8. Final Answer:
The number of persons present in the meeting is:
n=12
We know that in a meeting, every person shakes hands with every other person. The total number of handshakes is given as 66.
Let the total number of persons in the meeting be denoted by n. The number of ways to choose 2 persons from n persons (which represents one handshake) is given by the combination formula (n2). This can be expressed as:
(n2)=n(n−1)2
According to the problem, this is equal to 66:
n(n−1)2=66
To eliminate the fraction, multiply both sides of the equation by 2:
n(n−1)=132
Rearranging gives us a quadratic equation:
n2−n−132=0
We need to factor the quadratic equation. We look for two numbers that multiply to -132 and add to -1. The numbers are -12 and 11. Thus, we can factor the equation as:
(n−12)(n+11)=0
Setting each factor to zero gives us:
n−12=0orn+11=0
This results in:
n=12orn=−11
Since n represents the number of persons, it cannot be negative. Therefore, we discard n=−11.
The number of persons present in the meeting is:
n=12
Topper's Solved these Questions
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section B Objective type questions (One option is correct )
39 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section C Objective type questions (One option is correct )
17 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Try Yourself
65 Videos
- MATRICESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATRICESEXERCISE - Assignment (Section - J) Aakash Challengers Questions
3 Videos
- PRINCIPLE OF MATHEMATICAL BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PRINCIPLE OF MATHEMATICAL EXERCISE - Section-D:(Assertion-Reason Type Questions)
11 Videos
Similar Questions
Knowledge Check
Every body in a room shakes hands with everybody else. The total number of handshakes is 21. The total number of persons in the room is
A(a) 6B(b) 7C(c) 8D(d) 9At the end of a meeting all participants shook hands with each other. Twenty-eight handshakes were exchanged. How many people were at the meeting?
A7B8C14D28John decided to treat his friends with some chocolates. On visiting a Hershey's outlet, he found that chocolates were sold in boxes. The boxes had different number of chocolates and the prices of the boxes were also different. The prices are shown in the table below.

How much less does John spend if he busy 90 chocolates in boxes of 15 chocolates than if he buys the same in boxes of 10 chocolates ?A1.4B2.4C3.6D6
Twelve persons meet in a room and each shakes hand with all others. Find the number oif hand shakes.
View SolutionIn a family, father had a trait but mother did not. All their sons and daughters had this trait. The same trait was found in some grand daughters, through daughters were married to normal persons.
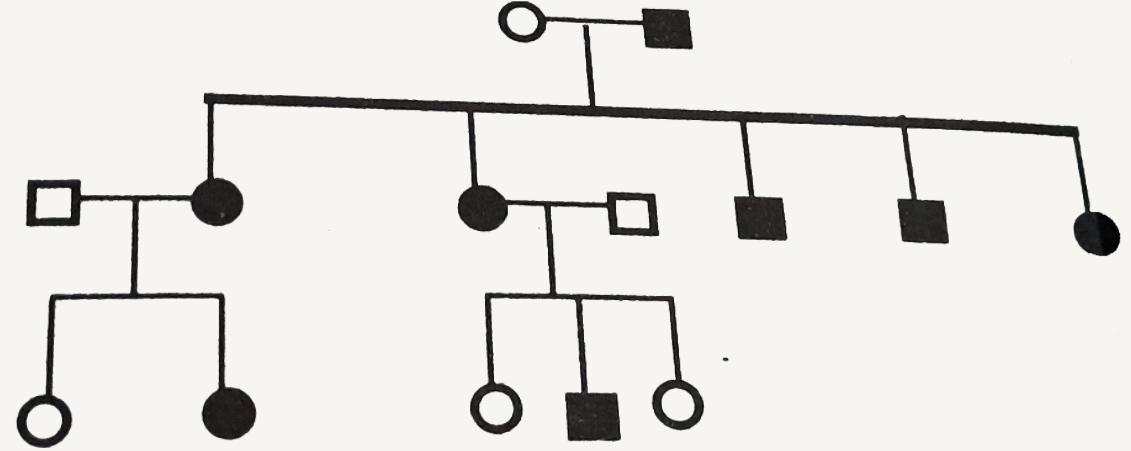
In this pedigree the genotypes of father, mother and husbands of daughters are
View Solution5 Indian & 5 American couples meet at a party& shake hands. If no wife shakes hands with her own husband & no Indian wife shakes hands with a male, then the number of hand shakes that takes place in an party
View SolutionThe hotel bill for a number of persons for overnight stay is Rs 4,800 If there were four more persons, the bill each person had to pay would have reduced by Rs 200. Find the number of persons staying overnight.
View SolutionNatalie is plannin a school celebration and wants to have live music and food for everyone who attends. She has found a band that will charge her $750 and a caterer who will provide snacks and drinks for $2.25 per person. If her goal is to keep the average cost per person between $2.75 and $3.25, how many people, p, must attend?
View Solution
