Let A=[ω−ω−ωω] where w is a complex cube root of unity, B=[(1,−1),(−1,1)andA9=2kB , where k=....
The correct Answer is:8
To solve the problem, we need to calculate A9 where A=(ω−ω−ωω) and ω is a complex cube root of unity. We also need to show that A9=2kB for some integer k, where B=(1−1−11).
Step 1: Understand the properties of ω
Since ω is a cube root of unity, we have:
ω3=1and1+ω+ω2=0
Step 2: Calculate A2
We will first calculate A2:
A2=A⋅A=(ω−ω−ωω)(ω−ω−ωω)
Calculating the elements:
- First row, first column: ω⋅ω+(−ω)(−ω)=ω2+ω2=2ω2
- First row, second column: ω⋅(−ω)+(−ω)ω=−ω2−ω2=−2ω2
- Second row, first column: −ω⋅ω+ω(−ω)=−ω2−ω2=−2ω2
- Second row, second column: −ω⋅(−ω)+ω⋅ω=ω2+ω2=2ω2
Thus, we have:
A2=(2ω2−2ω2−2ω22ω2)
Step 3: Calculate A3
Next, we calculate A3=A2⋅A:
A3=(2ω2−2ω2−2ω22ω2)(ω−ω−ωω)
Calculating the elements:
- First row, first column: 2ω2⋅ω+(−2ω2)(−ω)=2ω3+2ω3=4
- First row, second column: 2ω2⋅(−ω)+(−2ω2)ω=−2ω3−2ω3=−4
- Second row, first column: −2ω2⋅ω+2ω2(−ω)=−2ω3−2ω3=−4
- Second row, second column: −2ω2⋅(−ω)+2ω2⋅ω=2ω3+2ω3=4
Thus, we have:
A3=(4−4−44)
Step 4: Calculate A6
Next, we calculate A6=(A3)2:
A6=(4−4−44)(4−4−44)
Calculating the elements:
- First row, first column: 4⋅4+(−4)(−4)=16+16=32
- First row, second column: 4⋅(−4)+(−4)⋅4=−16−16=−32
- Second row, first column: −4⋅4+4⋅(−4)=−16−16=−32
- Second row, second column: −4⋅(−4)+4⋅4=16+16=32
Thus, we have:
A6=(32−32−3232)
Step 5: Calculate A9
Now, we calculate A9=A6⋅A3:
A9=(32−32−3232)(4−4−44)
Calculating the elements:
- First row, first column: 32⋅4+(−32)(−4)=128+128=256
- First row, second column: 32⋅(−4)+(−32)⋅4=−128−128=−256
- Second row, first column: −32⋅4+32⋅(−4)=−128−128=−256
- Second row, second column: −32⋅(−4)+32⋅4=128+128=256
Thus, we have:
A9=(256−256−256256)
Step 6: Relate A9 to B
We know that:
B=(1−1−11)
We can express A9 as:
A9=256⋅(1−1−11)=256B
Step 7: Determine k
From the equation A9=2kB, we can see that:
256=28
Thus, k=8.
Final Answer
k=8
Since ω is a cube root of unity, we have:
ω3=1and1+ω+ω2=0
We will first calculate A2:
A2=A⋅A=(ω−ω−ωω)(ω−ω−ωω)
- First row, first column: ω⋅ω+(−ω)(−ω)=ω2+ω2=2ω2
- First row, second column: ω⋅(−ω)+(−ω)ω=−ω2−ω2=−2ω2
- Second row, first column: −ω⋅ω+ω(−ω)=−ω2−ω2=−2ω2
- Second row, second column: −ω⋅(−ω)+ω⋅ω=ω2+ω2=2ω2
A2=(2ω2−2ω2−2ω22ω2)
Next, we calculate A3=A2⋅A:
A3=(2ω2−2ω2−2ω22ω2)(ω−ω−ωω)
- First row, first column: 2ω2⋅ω+(−2ω2)(−ω)=2ω3+2ω3=4
- First row, second column: 2ω2⋅(−ω)+(−2ω2)ω=−2ω3−2ω3=−4
- Second row, first column: −2ω2⋅ω+2ω2(−ω)=−2ω3−2ω3=−4
- Second row, second column: −2ω2⋅(−ω)+2ω2⋅ω=2ω3+2ω3=4
A3=(4−4−44)
Next, we calculate A6=(A3)2:
A6=(4−4−44)(4−4−44)
- First row, first column: 4⋅4+(−4)(−4)=16+16=32
- First row, second column: 4⋅(−4)+(−4)⋅4=−16−16=−32
- Second row, first column: −4⋅4+4⋅(−4)=−16−16=−32
- Second row, second column: −4⋅(−4)+4⋅4=16+16=32
A6=(32−32−3232)
Now, we calculate A9=A6⋅A3:
A9=(32−32−3232)(4−4−44)
- First row, first column: 32⋅4+(−32)(−4)=128+128=256
- First row, second column: 32⋅(−4)+(−32)⋅4=−128−128=−256
- Second row, first column: −32⋅4+32⋅(−4)=−128−128=−256
- Second row, second column: −32⋅(−4)+32⋅4=128+128=256
A9=(256−256−256256)
We know that:
B=(1−1−11)
We can express A9 as:
A9=256⋅(1−1−11)=256B
From the equation A9=2kB, we can see that:
256=28
Thus, k=8.
k=8
Topper's Solved these Questions
- MATRICESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATRICESEXERCISE - Assignment (Section - H) Multiple True - False Type Questions
2 Videos
- MATRICESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATRICESEXERCISE - Assignment (Section - I) Subjective Type Questions
3 Videos
- MATRICESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATRICESEXERCISE - Assignment (Section - F) Matrix - Match Type Question
1 Videos
- MATHEMATICAL REASONINGBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATHEMATICAL REASONINGEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
- PERMUTATIONS AND COMBINATIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PERMUTATIONS AND COMBINATIONS EXERCISE - Assignment Section-J (Aakash Challengers Questions)
7 Videos
Similar Questions
If A=⎛⎜⎝1111ω2ω1ωω2⎞⎟⎠ where ω is a complex cube root of unity then adj−A equals
View SolutionIf A=[ω00ω], where ω is cube root of unity, then what is A100 equal to ?
View SolutionIf w is a complex cube root of unity. Show that ∣∣ ∣ ∣∣1ww2ww21w21w∣∣ ∣ ∣∣=0 .
View SolutionIf ω is a cube root of unity, then
1+ω= …..
View SolutionEvaluate ∣∣ ∣ ∣∣1ωω2ωω21ω2ωω∣∣ ∣ ∣∣ where ω is cube root of unity.
View SolutionIf ω is a cube root of unity, then
1+ω2= …..
View Solution1a+ω+1b+ω+1c+ω+1d+ω=1ω where, a,b,c,d, ∈ R and ω is a complex cube root of unity then find the value of ∑1a2−a+1
View SolutionIf 1,ω,ω2 are three cube roots of unity, prove that
(1−ω)(1−ω2)=3
View SolutionIf 1,ω,ω2 are the cube roots of unity, then △
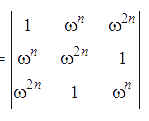
is equal to.....
View SolutionProve that the value of determinant ∣∣ ∣ ∣∣1ωω2ωω21ω21ω∣∣ ∣ ∣∣=0
where ω is complex cube root of unity .
View Solution
