If atmosphere pressure at a height of h units is given by the function then pressure is maximum at the height of
1 unit
units
e units
2 units
The correct Answer is:A
To find the height at which atmospheric pressure is maximum, we will follow these steps:
Step 1: Define the function
The atmospheric pressure at a height h is given by the function:
P(h)=he−h
Step 2: Differentiate the function
To find the maximum pressure, we need to find the derivative of P(h) with respect to h:
P′(h)=ddh(he−h)
Using the product rule, where u=h and v=e−h:
P′(h)=u′v+uv′=(1)(e−h)+(h)(−e−h)=e−h−he−h
Thus, we have:
P′(h)=e−h(1−h)
Step 3: Set the derivative to zero
To find the critical points, we set the derivative equal to zero:
e−h(1−h)=0
Since e−h is never zero, we can focus on:
1−h=0⟹h=1
Step 4: Determine if it is a maximum
To confirm that this point is a maximum, we need to find the second derivative P′′(h):
P′′(h)=ddh(P′(h))=ddh(e−h(1−h))
Using the product rule again:
P′′(h)=(−e−h)(1−h)+e−h(−1)=−e−h(1−h)−e−h=−e−h(2−h)
Now, we evaluate the second derivative at h=1:
P′′(1)=−e−1(2−1)=−e−1
Since −e−1<0, this indicates that P(h) has a local maximum at h=1.
Conclusion
The atmospheric pressure is maximum at a height of:
1
The atmospheric pressure at a height h is given by the function:
P(h)=he−h
To find the maximum pressure, we need to find the derivative of P(h) with respect to h:
P′(h)=ddh(he−h)
Using the product rule, where u=h and v=e−h:
P′(h)=u′v+uv′=(1)(e−h)+(h)(−e−h)=e−h−he−h
Thus, we have:
P′(h)=e−h(1−h)
To find the critical points, we set the derivative equal to zero:
e−h(1−h)=0
Since e−h is never zero, we can focus on:
1−h=0⟹h=1
To confirm that this point is a maximum, we need to find the second derivative P′′(h):
P′′(h)=ddh(P′(h))=ddh(e−h(1−h))
Using the product rule again:
P′′(h)=(−e−h)(1−h)+e−h(−1)=−e−h(1−h)−e−h=−e−h(2−h)
P′′(1)=−e−1(2−1)=−e−1
Since −e−1<0, this indicates that P(h) has a local maximum at h=1.
The atmospheric pressure is maximum at a height of:
1
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Assignment SECTION-B( Objective Type Questions ( One option is correct ))31videos
APPLICATION OF DERIVATIVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - Assignment SECTION-C( Objective Type Questions ( More than one option are correct ))1videos
APPLICATION OF DERIVATIVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF DERIVATIVESEXERCISE - TRY YOURSELF39videos
APPLICATION OF DERIVATIVES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF INTEGRALS EXERCISE - Assignment Section - I Aakash Challengers Questions2videos
APPLICATION OF INTEGRALS
Similar Questions
Variation of atmospheric pressure, with height from earth is
View SolutionAn air bubble of radius r in water is at a depth h below the water surface at some instant. If P is atmospheric pressure, d and T are density and surface tension of water respectively . the pressure inside the bubble will be :
View Solution
Knowledge Check
- Question 1 - Select One
A model rocket is launched vertically into the air such that its height at any time, t, is given by the function h(t)=−16t2+80t+10. What is the maximum height attained by the model rocket?
A140B110C85D10 - Question 2 - Select One
The pressure at depth h below the surface of a liquid of density ρ open to the atmosphere is
Agreater than the atmospheric pressure by ρghBless than the atmospheric pressure by ρghCequal to the atmospheric pressureDincreases exponentially with depth - Question 3 - Select One
If the sum of the heights of transmitting and receiving antennas in line of sight of communication is fixed at h, show that the range is maximum when the two antennas have a height h/2 each.
Ah/2B2hChD4h
The atmospheric pressure and height of barometer column is 105Pe and 760 mm respectively on the earth surface. If the barometer is taken to the moon then column height will be-
View SolutionAn altimeter is an aneroid barometer which makes use of the change in atmospheric pressure with the change in height above the sea level (altitude).
How does the atmospheric pressure change with increase in height above the sea level?View SolutionA storage tower supplies water, as shown in the figure. If P0 is the atmospheric pressure h = height of water level, g = acceleration due to gravity, ρ= density and v = velocity of flow in the horizontal pipe at B, then the pressure at B is -
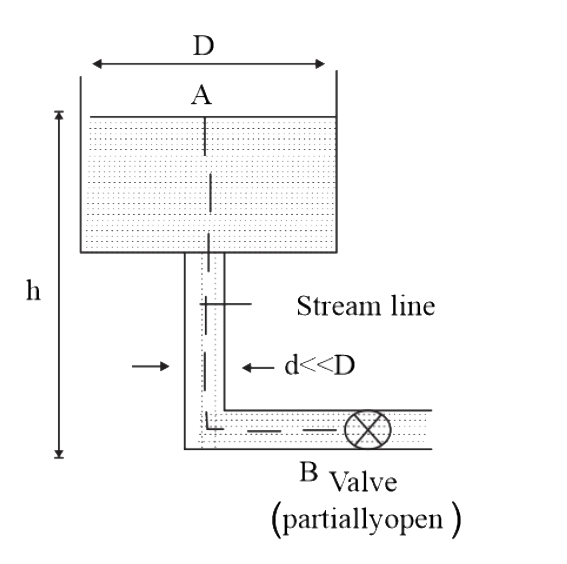 View Solution
View SolutionA tube of uniform cross section is used to siphon water from a vessel V as shown in the figure. The pressure over the open end of water in the vessel is atmospheric pressure (P0). The height of the tube above and below the water level in the vessel are h1 and h2, respectively.
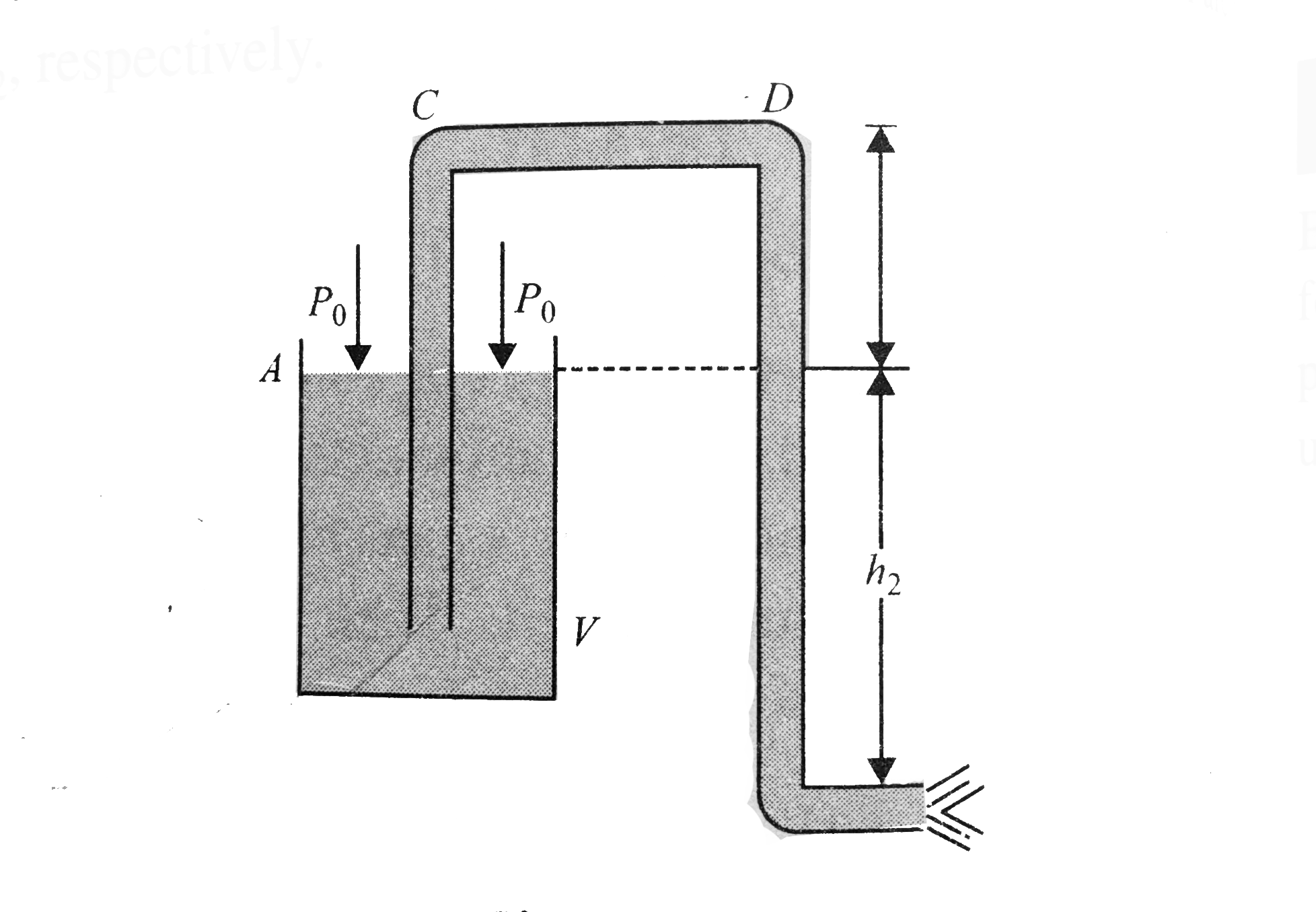
If h1=h2=3.0m, the maximum value of h1, for which the siphon will work will beView SolutionA cylindrical tank contains water up to a height H. If the tank is accelerated upwards with acceleration a, the pressure at the A is p1. If the tank is accelerated downwards with acceleration a the pressure at A is p2. Then
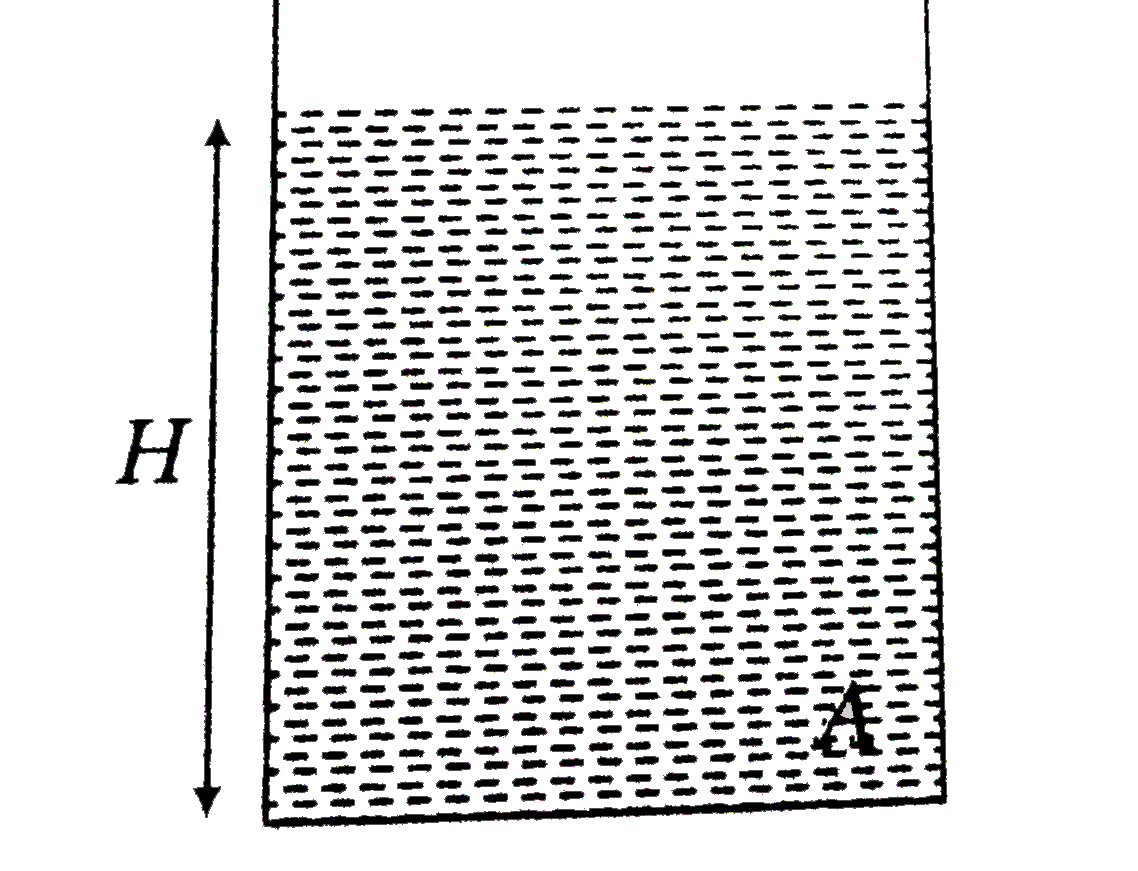 View Solution
View Solution

