Doubtnut Promotions Sticky

Let the function defined in Colomn-I have domain (0,π2) then match the following
Let the function defined in Colomn-I have domain (0,(pi)/(2)) then match the following

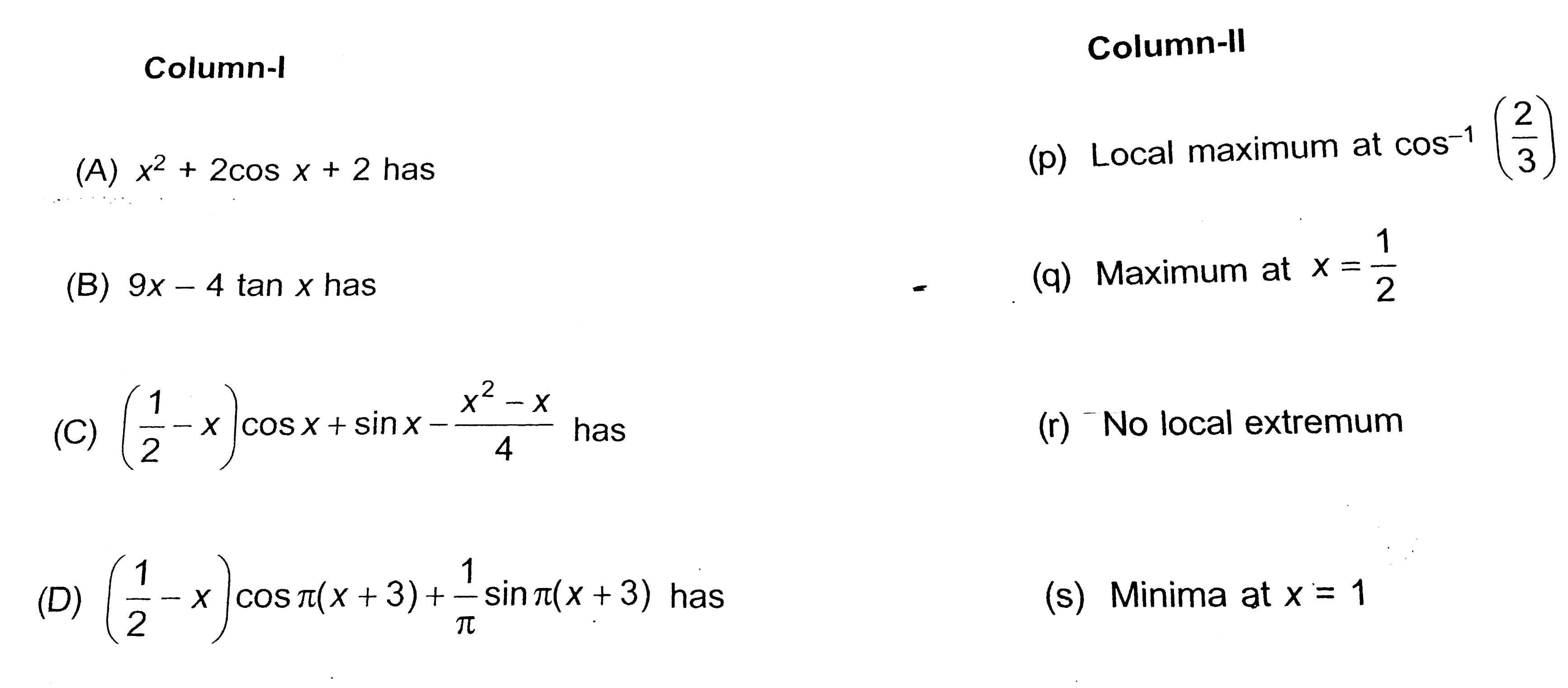
Text Solution
Verified by Experts

A(r), B(p), C(q), D(q,s)

Doubtnut Promotions Banner
|
Updated on:21/07/2023
Class 12MATHSAPPLICATION OF DERIVATIVES

Topper's Solved these Questions

Similar Questions

Knowledge Check

  • Question 1 - Select One

    Let f be the function defined on R as follows

    Af is continuous at 0
    Bf is discontinuous at 0
    Cf is nowhere at 0
    Df is everywhere discontinuous
  • Question 2 - Select One or More

    Let the function f(x)=sinx+cosx, be defined in [0,2π], then f(x)

    Aincreases in (π/4,π/2)
    Bdecreases in [π/4,5π/4]
    Cincreases in [0,π/4]∪[5π/4,2π]
    Ddecreases in [0,π/4)∪(π/2,2π]
  • Question 3 - Select One or More

    Let f:I−{−1,0,1}→[−π,π] be defined as f(x)=2tan−1x−tan−1(2x1−x2), then which of the following statements (s) is (are) correct ?

    Af(x) is bijective
    Bf(x) is injective but not surjective
    Cf(x) is neither injective nor surjective
    Df(x) is an odd function