The intersection of XY-plane and YZ-plane is known as
x-axis
y-axis
z-axis
Origin
The correct Answer is:B
To solve the question, "The intersection of XY-plane and YZ-plane is known as," we can follow these steps:
1. Understanding the Planes:
- The XY-plane is defined by the equation z=0. This means that any point on this plane has a z-coordinate of 0.
- The YZ-plane is defined by the equation x=0. This means that any point on this plane has an x-coordinate of 0.
2. Finding the Intersection:
- The intersection of two planes is generally a line. To find the intersection of the XY-plane and YZ-plane, we need to find the common points that satisfy both equations.
- From the XY-plane, we have z=0.
- From the YZ-plane, we have x=0.
3. Setting Up the Intersection:
- For the intersection, we can set x=0 (from the YZ-plane) and z=0 (from the XY-plane).
- The coordinates of the points on the intersection line can be represented as (0,y,0), where y can take any value.
4. Identifying the Line:
- The points (0,y,0) indicate that the intersection line lies along the Y-axis in the three-dimensional coordinate system.
- Therefore, the intersection of the XY-plane and YZ-plane is the Y-axis.
5. Conclusion:
- We conclude that the intersection of the XY-plane and YZ-plane is known as the Y-axis.
Final Answer:
The intersection of the XY-plane and YZ-plane is known as the Y-axis.
---
- The XY-plane is defined by the equation z=0. This means that any point on this plane has a z-coordinate of 0.
- The YZ-plane is defined by the equation x=0. This means that any point on this plane has an x-coordinate of 0.
- The intersection of two planes is generally a line. To find the intersection of the XY-plane and YZ-plane, we need to find the common points that satisfy both equations.
- From the XY-plane, we have z=0.
- From the YZ-plane, we have x=0.
- For the intersection, we can set x=0 (from the YZ-plane) and z=0 (from the XY-plane).
- The coordinates of the points on the intersection line can be represented as (0,y,0), where y can take any value.
- The points (0,y,0) indicate that the intersection line lies along the Y-axis in the three-dimensional coordinate system.
- Therefore, the intersection of the XY-plane and YZ-plane is the Y-axis.
- We conclude that the intersection of the XY-plane and YZ-plane is known as the Y-axis.
The intersection of the XY-plane and YZ-plane is known as the Y-axis.
Topper's Solved these Questions
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - B
47 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - C
14 Videos
- THREE DIMENSIONAL GEOMETRY BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - TRY YOURSELF
97 Videos
- STRAIGHT LINESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)
5 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
16 Videos
Similar Questions
Knowledge Check
x-axis is the intersection of two planes
Axy and yzByz and zxCsecond octantDeithth octant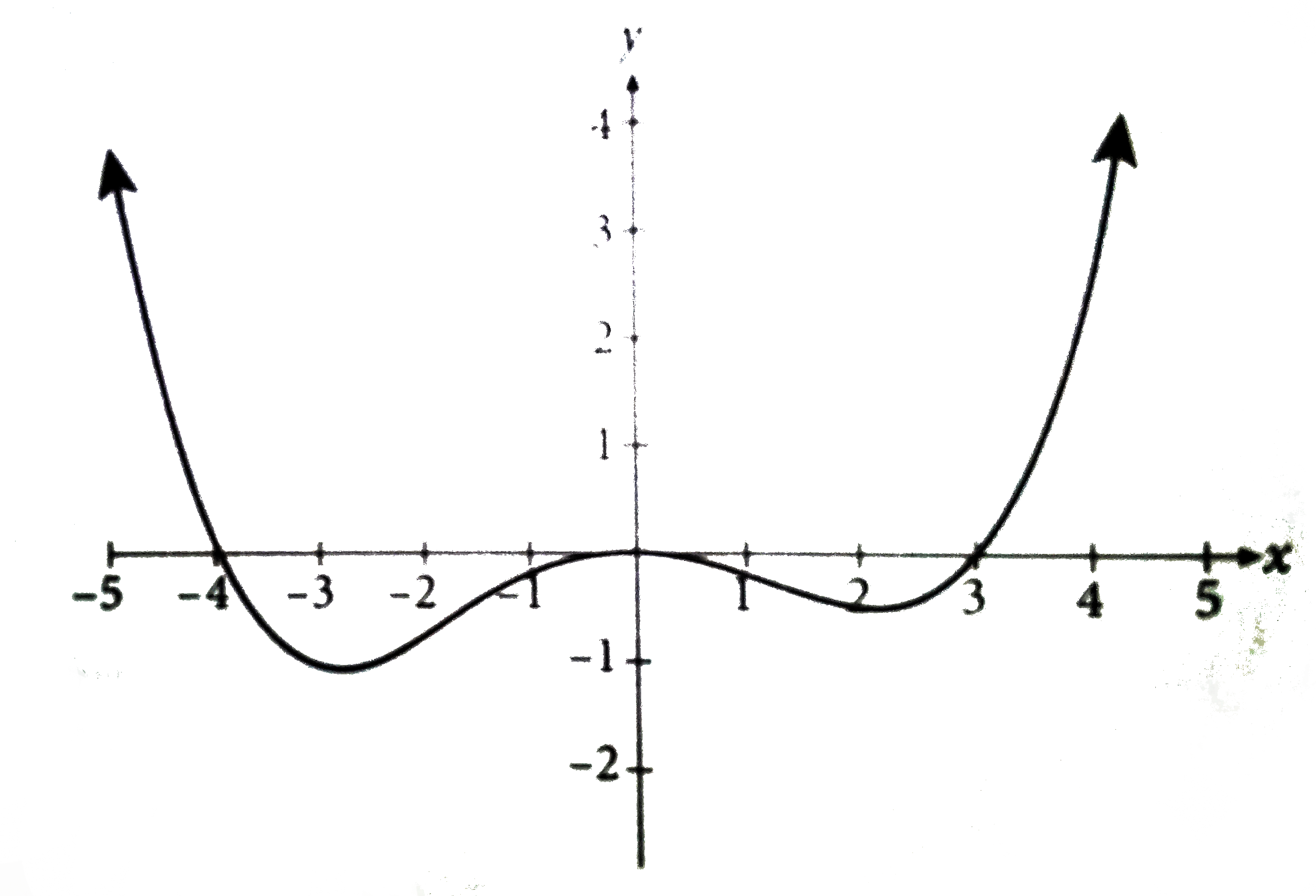
Which of the following could be the equation of the graph in the xy-plane shown above?Af(x)=x(x+3)(x−4)Bf(x)=x(x+4)(x−3)Cf(x)=x2(x+3)(x−4)Df(x)=x2(x+4)(x−3)
The minimum number of points of intersection of three lines drawn in a plane is
View SolutionThe maximum number of points of intersections of three lines drawn in a plane is
View SolutionIf a point P lies in YZ- plane , then the coordinates of a point on YZ-plane is the form…………
View SolutionTwo infinitely large charged planes having uniform surface change density +σ and -σ are placed along xy plane and yz plane resp as shown in figure. Then nature of electric lines of force in xz plane is given by

View SolutionConsider a plane P:2x+y−z=5, a line L:x−32=y+1−3=z−2−1 and a point A(3,−4,1). If the line L intersects plane P at B and the xy plane at C, then the area (in sq. units) of ΔABC is
View SolutionConsider a plane ∏:→r⋅(2ˆi+ˆj−ˆk)=5, a line L1:→r=(3ˆi−ˆj+2ˆk)+k(2ˆi−3ˆj−ˆk) and a point A(3,−4,1)⋅L2 is a line passing through A intersecting L1 and parallel to plane ∏.
Q. Line L1 intersects plane ∏ at Q and xy-plane at R the volume of tetrahedron OAQR is :
(where 'O' is origin)
View Solution
