Let P1andP2 be two planes containing the lines L2andL2 respectively.
STATEMENT-1 : If P1andP2 are parallel then L1andL2 must be parallel.
and
STATEMENT-2 : If P1andP2 are parallel the L1andL2 may not have a common point.
Statement-1 is True, Statement-2 is true, Statement- is a correct explanation for Statement -1
Statement-1 is True, Statement-2 is true, Statement- is NOT a correct explanation for Statement -1
Statement-1 is True, Statement-2 is False
Statement-1 is False, Statement-2 is true
The correct Answer is:D
To solve the problem, we need to analyze the two statements regarding the planes P1 and P2 and the lines L1 and L2 contained within them.
Step 1: Understanding the Relationship Between Planes and Lines
We are given two planes P1 and P2 that are parallel. By definition, if two planes are parallel, they do not intersect.
Hint: Remember that parallel planes have the same normal vector and do not meet at any point.
Step 2: Analyzing Statement 1
Statement 1: If P1 and P2 are parallel, then L1 and L2 must be parallel.
This statement is false. While the planes are parallel, the lines contained in them can be oriented in different directions. For instance, L1 could be slanted in one direction while L2 could be slanted in another direction, leading to them being skew lines (not parallel and not intersecting).
Hint: Consider the possibility of skew lines existing in parallel planes.
Step 3: Analyzing Statement 2
Statement 2: If P1 and P2 are parallel, then L1 and L2 may not have a common point.
This statement is true. Since the planes do not intersect, the lines contained within them can either be parallel (and thus do not intersect) or skew (not parallel and also do not intersect). In both cases, they do not have a common point.
Hint: Think about the definitions of parallel and skew lines and how they relate to the planes.
Conclusion
- Statement 1 is false: L1 and L2 do not have to be parallel even if P1 and P2 are parallel.
- Statement 2 is true: L1 and L2 may not have a common point when P1 and P2 are parallel.
Final Answer:
- Statement 1: False
- Statement 2: True
We are given two planes P1 and P2 that are parallel. By definition, if two planes are parallel, they do not intersect.
Statement 1: If P1 and P2 are parallel, then L1 and L2 must be parallel.
Statement 2: If P1 and P2 are parallel, then L1 and L2 may not have a common point.
- Statement 1 is false: L1 and L2 do not have to be parallel even if P1 and P2 are parallel.
- Statement 2 is true: L1 and L2 may not have a common point when P1 and P2 are parallel.
- Statement 1: False
- Statement 2: True
Topper's Solved these Questions
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - F4videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - G7videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - THREE DIMENSIONAL GEOMETRY EXERCISE - ASSIGNMENT SECTION - D COMPREHENSION VI3videos
THREE DIMENSIONAL GEOMETRY
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - STRAIGHT LINESEXERCISE - SECTION-J (AAKASH CHALLENGERS QUESTIONS)5videos
STRAIGHT LINES
- BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)16videos
TRIGNOMETRIC FUNCTIONS
Similar Questions
Consider three planes P1:x−y+z=1, P2:x+y−z=−1 and
P3:x−3y+3z=2. Let L1,L2,L3 be the lines of intersection of the planes P2 and P3,P3 and P1,P1 and P2 respectively.
Statement I Atleast two of the lines L1,L2 and L3 are non-parallel.
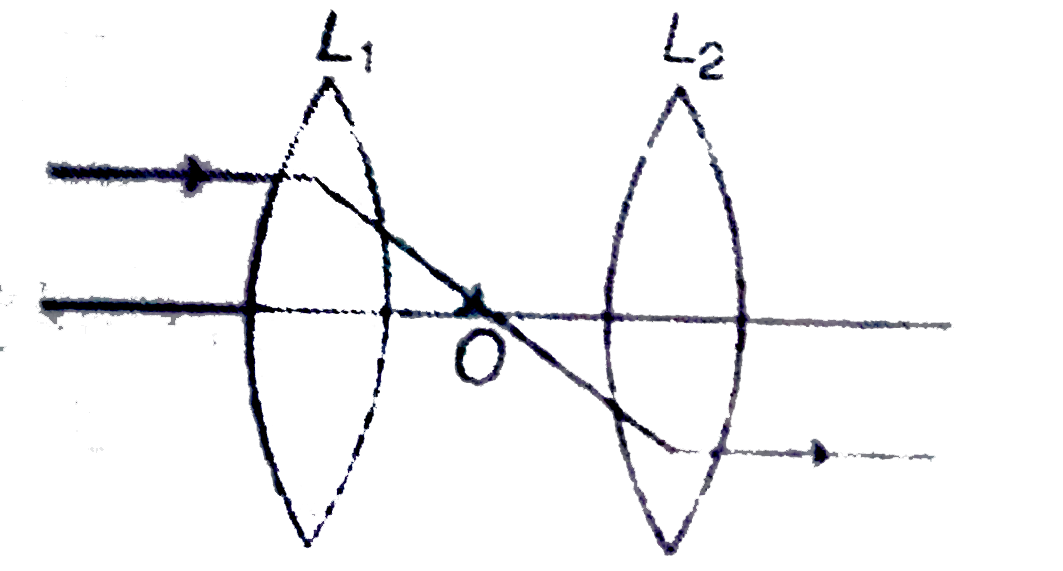
Statement II The three planes do not have a common point.View SolutionIn the figure shown, there are two convex lenses L1 and L2 having focal. Lengths f1 and f2 respectively. The distance between L1 and L2 will be
 View Solution
View SolutionLet l1 and l2 be the two lines which are normal to y2=4x and tangent to x2=−12y respectively (where, l1andl2 are not the x - axis). Then, the product of the slopes of l1andl2 is
View SolutionConsider three planes P1:x−y+z=1, P2:x+y−z=−1 and P3:x−3y+3z=2 Let L1,L2 and L3 be the lines of intersection of the planes P2andP3, P3andP1 and P1andP2 respectively.Statement 1: At least two of the lines L1,L2andL3 are non-parallel . Statement 2:The three planes do not have a common point
View SolutionLet L be the set of all straight lines in plane. l1 and l2 are two lines in the set. R1,R2 and R3 are defined relations.
(i) l1R1l2:l1 is parallel to l2
(ii) l1R2l2:l1 is perpendicular to l2
(iii) l1R3l2:l1 intersects l2
Then which of the following is true ?View SolutionLet ∠1and∠2 be two lines such that
L2:x+1−3=y−32=z+21,L2:x1=y−7−3=z+72
Equation of a plane containing ∠1and∠2 isView SolutionLet l1andl2 be the two skew lines. If P, Q are two distinct points on l1 and R, S are two distinct points on l2, then prove that PR cannot be parallel to QS.
View SolutionConsider two intersecting (non-perpendicular lines L1=0andL2=0 and a point P1. Image of P1 and L1=0 is P2, image of P2 in L2=0 is P3 , image of P3 in L1 =0 is P4 and so on. Which of the following statements are incorrect ?
View SolutionLet L1=0andL2=0 be two intarecting straight lines. Then the number of points, whose distacne from L1 is 2 units and from L2 2 units is
View SolutionA line L1 with direction ratios −3,2,4 passes through the point A(7,6,2) and a line L2 with directions ratios 2,1,3 passes through the point B(5,3,4). A line L3 with direction ratios 2,−2,−1 intersects L1 and L3 at C and D, resectively. The equation of the plane parallel to line L1 and containing line L2 is equal to
View Solution

