ABCDEF is a regular hexagon where centre O is the origin, if the position vector of A is ˆi−ˆj+2ˆk, then ¯¯¯¯¯¯BC is equal to
ˆi−ˆj+2ˆk
−ˆi+ˆj−2ˆk
3ˆi+3ˆj−4ˆk
Both (1) & (2)
The correct Answer is:2
To find the vector ¯¯¯¯¯¯¯¯BC in the regular hexagon ABCDEF with the center O at the origin and the position vector of point A given as ^i−^j+2^k, we can follow these steps:
Step 1: Understand the Position Vector of A
The position vector of point A is given as:
→OA=^i−^j+2^k
Step 2: Determine the Position Vector of O
Since O is the origin, its position vector is:
→O=→0=0^i+0^j+0^k
Step 3: Find the Position Vector of A
The position vector of point A is:
→A=^i−^j+2^k
Step 4: Determine the Relationship Between Vectors
In a regular hexagon, the vectors from the center O to the vertices are equal in magnitude and are separated by angles of 60∘. The vector ¯¯¯¯¯¯¯¯OA represents one of these vectors.
Step 5: Find the Position Vector of B
Since O is the center and A is at an angle of 0∘, the position vector of B will be at an angle of 60∘ from OA. To find the position vector of B, we can rotate the vector OA by 60∘.
Using the rotation matrix for 60∘:
(cos(60∘)−sin(60∘)sin(60∘)cos(60∘))=⎛⎜⎝12−√32√3212⎞⎟⎠
Step 6: Apply the Rotation to Find B
We can express the vector →A in terms of its components:
→A=⎛⎜⎝1−12⎞⎟⎠
Now, applying the rotation matrix to the x and y components:
(xByB)=⎛⎜⎝12−√32√3212⎞⎟⎠(1−1)=⎛⎜⎝12+√32√32−12⎞⎟⎠
Calculating this gives:
xB=1+√32,yB=√3−12
Step 7: Find the Position Vector of C
Continuing this process, we can find the position vector of C by rotating B by another 60∘.
Step 8: Calculate Vector ¯¯¯¯¯¯¯¯BC
The vector ¯¯¯¯¯¯¯¯BC can be calculated as:
→BC=→C−→B
Final Step: Write the Result
After calculating the vectors, we find that:
¯¯¯¯¯¯¯¯BC=−^i+^j−2^k
Thus, the vector ¯¯¯¯¯¯¯¯BC is:
¯¯¯¯¯¯¯¯BC=−^i+^j−2^k
The position vector of point A is given as:
→OA=^i−^j+2^k
Since O is the origin, its position vector is:
→O=→0=0^i+0^j+0^k
The position vector of point A is:
→A=^i−^j+2^k
In a regular hexagon, the vectors from the center O to the vertices are equal in magnitude and are separated by angles of 60∘. The vector ¯¯¯¯¯¯¯¯OA represents one of these vectors.
Since O is the center and A is at an angle of 0∘, the position vector of B will be at an angle of 60∘ from OA. To find the position vector of B, we can rotate the vector OA by 60∘.
(cos(60∘)−sin(60∘)sin(60∘)cos(60∘))=⎛⎜⎝12−√32√3212⎞⎟⎠
We can express the vector →A in terms of its components:
→A=⎛⎜⎝1−12⎞⎟⎠
(xByB)=⎛⎜⎝12−√32√3212⎞⎟⎠(1−1)=⎛⎜⎝12+√32√32−12⎞⎟⎠
xB=1+√32,yB=√3−12
Continuing this process, we can find the position vector of C by rotating B by another 60∘.
The vector ¯¯¯¯¯¯¯¯BC can be calculated as:
→BC=→C−→B
After calculating the vectors, we find that:
¯¯¯¯¯¯¯¯BC=−^i+^j−2^k
¯¯¯¯¯¯¯¯BC=−^i+^j−2^k
Topper's Solved these Questions
- VECTOR ALGEBRABOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - ASSIGNMENT (SECTION-B)
32 Videos
- VECTOR ALGEBRABOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - ASSIGNMENT (SECTION-C)
6 Videos
- VECTOR ALGEBRABOOK - AAKASH INSTITUTE ENGLISHCHAPTER - VECTOR ALGEBRAEXERCISE - TRY YOURSELF
20 Videos
- TRIGNOMETRIC FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - TRIGNOMETRIC FUNCTIONS EXERCISE - Section - J (Akash Challengers Question)
16 Videos
Similar Questions
Knowledge Check
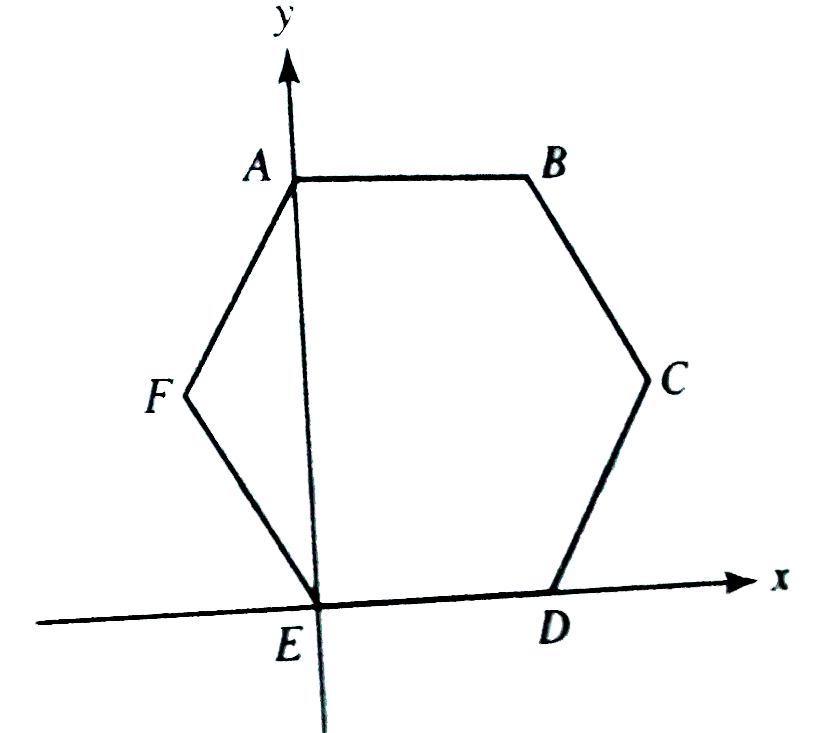
ABCDEF is a regular hexagon . What is the slope of the line containing ¯¯¯¯¯¯FE ?A−12B−√3C−√2D√3
The angular velocity of a particle is →w=4ˆi+ˆj−2ˆk about the origin. If the position vector of the particle is 2ˆi+3ˆj−3ˆk, then its linear velocity is
View SolutionFind the vector area of the triangle, the position vectors of whose vertices are ˆi+ˆj+2ˆk,2ˆi+2ˆj−3ˆkand3ˆi−ˆj−ˆk
View SolutionIf θ is the angle between the vectors 2ˆi−2ˆj+4ˆk and 3ˆi+ˆj+2ˆk, then sinθ is equal to
View SolutionIf ABCDEF is a regular hexagon with −−→AB=→a and −−→BC=→b, then −−→CE equals
View SolutionConsider the regular hexagon ABCDEF with centre at O (origin).
Q. AD+EB+FC is equal to
View SolutionIf ABCDEF is a regular hexagon then −−→AD+−−→EB+−−→FC equals :
View SolutionA unit vector perpendicular to the plane passing through the points whose position vectors are ˆi−ˆj+2ˆk,2ˆi−ˆk and 2ˆi+ˆk is
View Solution
