The maximum angle to the horizontal at which a stone can be thrown so that it always moves away from the thrower will be :
The correct Answer is:sin−1(√89
To solve the problem of finding the maximum angle to the horizontal at which a stone can be thrown so that it always moves away from the thrower, we can follow these steps:
1. Understanding the Problem:
We need to determine the maximum angle θ at which a stone can be thrown such that it always moves away from the thrower. This means that the radial distance from the thrower to the stone must always increase.
2. Defining the Motion:
When the stone is thrown with an initial velocity V at an angle θ, it has two components of velocity:
- Horizontal component: Vx=Vcosθ
- Vertical component: Vy=Vsinθ
3. Position Vector:
The position vector r of the stone at time t can be expressed as:
r=(Vcosθ)t^i+(Vsinθt−12gt2)^j
4. Velocity Vector:
The velocity vector v at time t is given by:
v=Vcosθ^i+(Vsinθ−gt)^j
5. Condition for Moving Away:
For the stone to always move away from the thrower, the dot product of the position vector r and the velocity vector v must be positive:
r⋅v>0
6. Calculating the Dot Product:
r⋅v=(Vcosθt)(Vcosθ)+(Vsinθt−12gt2)(Vsinθ−gt)
Expanding this gives us:
=V2cos2θt+(Vsinθt−12gt2)(Vsinθ−gt)
7. Simplifying the Expression:
After simplification, we need to ensure that the resulting expression is always greater than zero. This leads to a quadratic inequality in t.
8. Finding Conditions on θ:
For the quadratic expression to be always positive, we analyze the coefficients. The discriminant of the quadratic must be less than zero:
9/8V2sin2θ<V2
9. Solving for θ:
Rearranging gives:
sin2θ<89⟹sinθ<2√23
Thus, the maximum angle θ can be found using:
θ<sin−1(2√23)
10. Final Answer:
The maximum angle θ at which the stone can be thrown so that it always moves away from the thrower is:
θ=sin−1(2√23)
We need to determine the maximum angle θ at which a stone can be thrown such that it always moves away from the thrower. This means that the radial distance from the thrower to the stone must always increase.
When the stone is thrown with an initial velocity V at an angle θ, it has two components of velocity:
- Horizontal component: Vx=Vcosθ
- Vertical component: Vy=Vsinθ
The position vector r of the stone at time t can be expressed as:
r=(Vcosθ)t^i+(Vsinθt−12gt2)^j
The velocity vector v at time t is given by:
v=Vcosθ^i+(Vsinθ−gt)^j
For the stone to always move away from the thrower, the dot product of the position vector r and the velocity vector v must be positive:
r⋅v>0
r⋅v=(Vcosθt)(Vcosθ)+(Vsinθt−12gt2)(Vsinθ−gt)
Expanding this gives us:
=V2cos2θt+(Vsinθt−12gt2)(Vsinθ−gt)
After simplification, we need to ensure that the resulting expression is always greater than zero. This leads to a quadratic inequality in t.
For the quadratic expression to be always positive, we analyze the coefficients. The discriminant of the quadratic must be less than zero:
9/8V2sin2θ<V2
Rearranging gives:
sin2θ<89⟹sinθ<2√23
Thus, the maximum angle θ can be found using:
θ<sin−1(2√23)
The maximum angle θ at which the stone can be thrown so that it always moves away from the thrower is:
θ=sin−1(2√23)
Topper's Solved these Questions
- MOTION IN A PLANEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A PLANEEXERCISE - Assignement section -I (Subjective )
2 Videos
- MOCK_TEST_17BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOCK_TEST_17EXERCISE - Example
15 Videos
- MOTION IN A STRAIGHT LINEBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MOTION IN A STRAIGHT LINEEXERCISE - ASSIGNMENT (SECTION - D)
15 Videos
Similar Questions
The surface of a hill is inclined at an angle α to the horizontal .A stone is thrown from the summit of the hill at an angle β to the vertical with velocity v0.How far from the summit will the stone strike the ground ?
View SolutionA particle is thrown with velocity u at an angle ∝ from the horizontal. Another particle is thrown with the same velocity at an angle ∝ from the verticle. What will be the ratio of times of flight of two particles ?
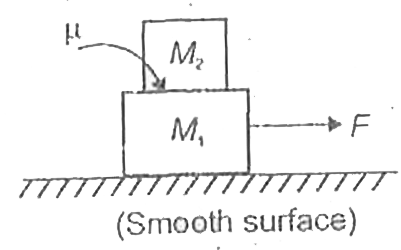
View SolutionThe maximum value of F which can be applied on the system shown in figure so that both blocks move together with same acceleration is
View SolutionA boy can throw a stone up to a maximum height of 10m. The maximum horizontal distance that the boy can throw the same stone up to will be :
View SolutionA boy can throw a stone up to a maximum height of 10m. The maximum horizontal distance that the boy can throw the same stone up to will be :
View SolutionA boy can throw a stone up to a maximum height of 10 m. The maximum horizontal distance that the boy can throw the same stone up to will be:
View SolutionA car moving on a horizontal road may be thrown out of the road in taking a turn
View SolutionA cricket ball is thrown at a speed of 28ms−1 in a direction 30∘ above the horizontal. Calculate (a)the maximum height (b) the time taken by ball to return to the same level, and (c )the distance from the thrower to the point where the ball returns to the same level.
View SolutionA stone is thrown at an angle θ to the horizontal reaches a maximum height H. Then the time of flight of stone will be:
View SolutionA stone is thrown at an angle θ to the horizontal reaches a maximum height H. Then the time of flight of stone will be:
View Solution
