Two circular coils have their centres at the same point. The mutual inductance between them will be maximum when their axes
Perpendicular to each other
At 60∘ to each other
At 45∘ to each other
Parallel to each other
The correct Answer is:D
To solve the problem of determining the orientation of two circular coils that maximizes their mutual inductance, we can follow these steps:
1. Understanding Mutual Inductance:
- Mutual inductance (M) between two coils is a measure of how much magnetic flux from one coil links with the other coil. It is influenced by the relative orientation of the coils.
2. Visualizing the Coils:
- Imagine two circular coils with their centers at the same point. We can visualize them in different orientations: parallel, perpendicular, or at angles to each other.
3. Analyzing Parallel Orientation:
- When the axes of the two coils are parallel to each other, the magnetic field lines produced by the primary coil will pass through the secondary coil effectively. This results in a maximum number of magnetic field lines linking the two coils.
4. Magnetic Flux Linking:
- The magnetic flux (Φ) linked with the secondary coil due to the primary coil can be expressed as:
Φ2=M⋅I1
where Φ2 is the magnetic flux linked with the secondary coil, M is the mutual inductance, and I1 is the current in the primary coil.
5. Maximizing Magnetic Flux:
- Since mutual inductance is directly proportional to the magnetic flux linked with the secondary coil, to maximize M, we need to maximize Φ2. This occurs when the coils are aligned parallel to each other.
6. Conclusion:
- Therefore, the mutual inductance between the two coils will be maximum when their axes are parallel to each other.
Final Answer:
The mutual inductance between the two circular coils will be maximum when their axes are parallel to each other.
- Mutual inductance (M) between two coils is a measure of how much magnetic flux from one coil links with the other coil. It is influenced by the relative orientation of the coils.
- Imagine two circular coils with their centers at the same point. We can visualize them in different orientations: parallel, perpendicular, or at angles to each other.
- When the axes of the two coils are parallel to each other, the magnetic field lines produced by the primary coil will pass through the secondary coil effectively. This results in a maximum number of magnetic field lines linking the two coils.
- The magnetic flux (Φ) linked with the secondary coil due to the primary coil can be expressed as:
Φ2=M⋅I1
where Φ2 is the magnetic flux linked with the secondary coil, M is the mutual inductance, and I1 is the current in the primary coil.
- Since mutual inductance is directly proportional to the magnetic flux linked with the secondary coil, to maximize M, we need to maximize Φ2. This occurs when the coils are aligned parallel to each other.
- Therefore, the mutual inductance between the two coils will be maximum when their axes are parallel to each other.
The mutual inductance between the two circular coils will be maximum when their axes are parallel to each other.
Topper's Solved these Questions
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - B)
22 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Assignment (SECTION - C)
10 Videos
- ELECTROMAGNETIC INDUCTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC INDUCTIONEXERCISE - Try Yourself
42 Videos
- ELECTRIC CHARGES AND FIELDS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTRIC CHARGES AND FIELDS EXERCISE - comprehension
3 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
Similar Questions
Define the term 'mutual inductance' between the two coils.
View SolutionFind the mutual inductance between two rectangular loops, shown in the figure.
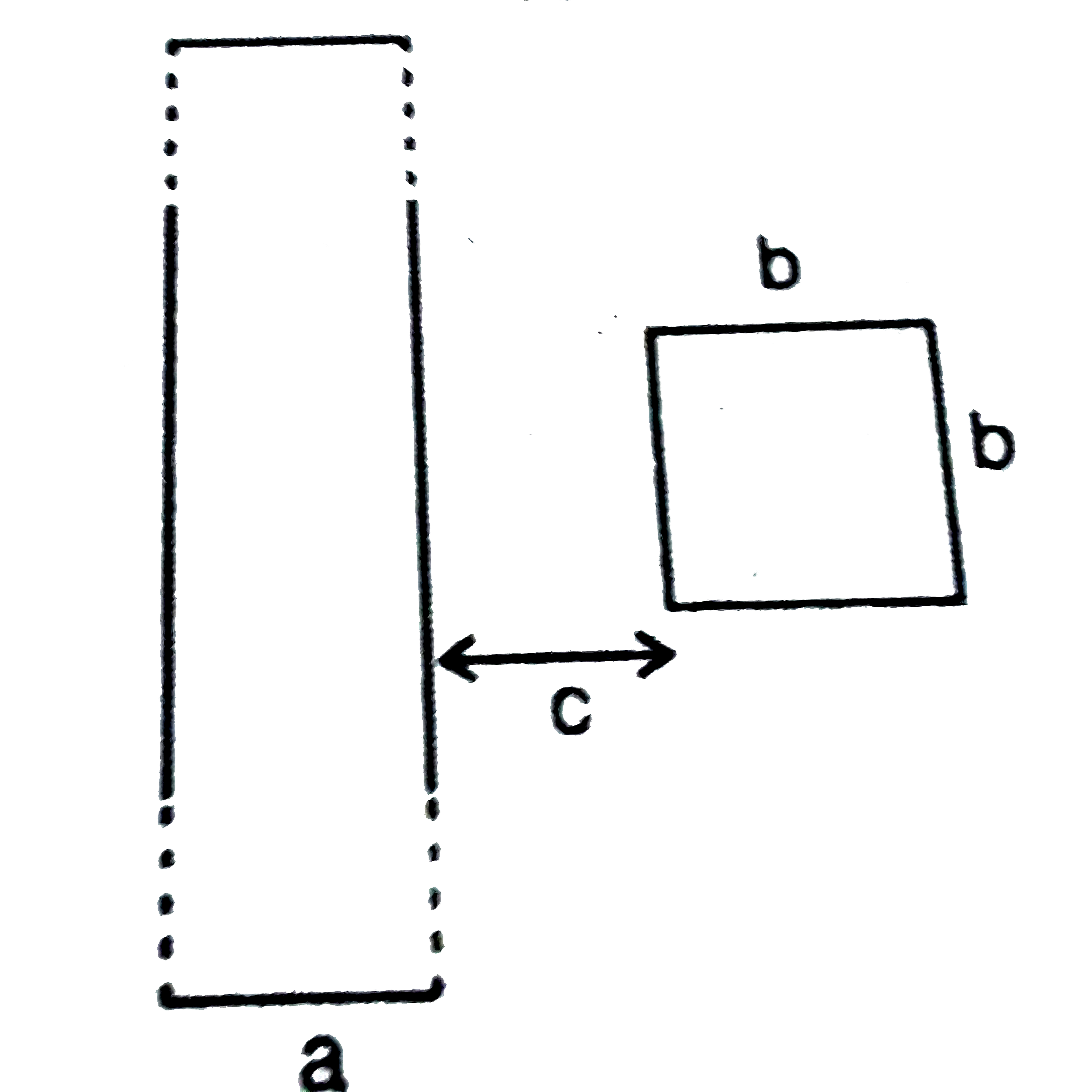
View SolutionFind the mutual inductance between two rectangular loops, shown in the figure.

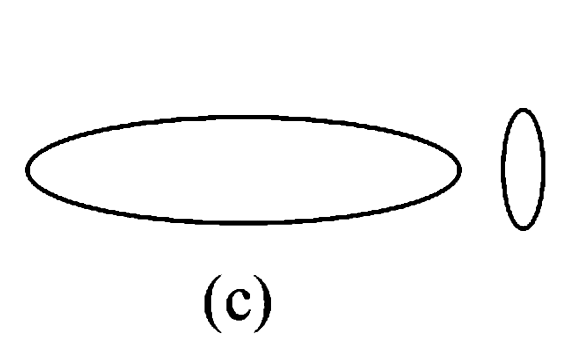
View SolutionTwo circular coils can be arranged in any of the three situation shown in the figure. Their mutual inductance will be

View SolutionThe mutual inductance of two coil of radii a and b (a<<
View SolutionTwo circular coils can be arranged in any of the three situation shown in the figure. Their mutual inductance will be
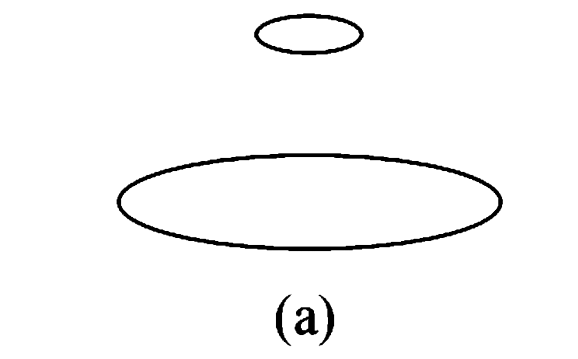 ,
, 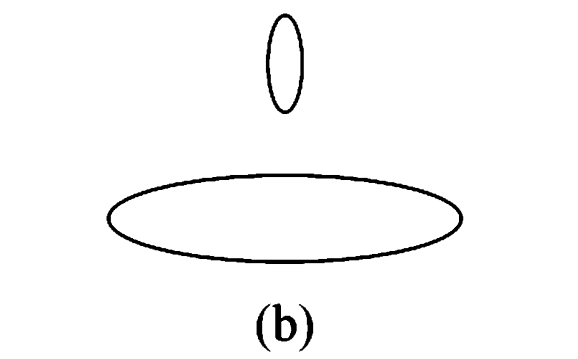 ,
, 
View SolutionTwo circular coils can be arranged in any of the three situations shown in the figure. Their mutual inductance will be
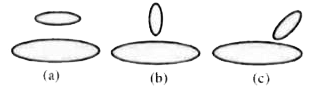
View SolutionThe current in a long solenoid of radius R and having n turns per unit length is given by i=i0sinωt. A coil having N turns is wound around it near the centre. Find (a) the induced emf in the coil and (b) the mutual inductance between the solenoid and the coil.
View SolutionName two factors on which mutual inductance between a pair of coils depends?
View SolutionThe conducting circular loops of radii R1andR2 are placed in the same plane with their centres coinciding. If R1>>R2, the mutual inductance M between them will be directly proportional to
View Solution
