If the frequency of applied source is increased, how will brightness change?
The correct Answer is:Brightness will decrease
To solve the problem of how brightness changes when the frequency of the applied source is increased, we can follow these steps:
1. Understand the Circuit Configuration:
- The circuit consists of a bulb (which represents a load) connected in series with an inductor (L) and a resistor (R). The brightness of the bulb is related to the power consumed in the circuit.
2. Identify the Impedance:
- The total impedance (Z) in the circuit can be expressed as:
Z=√R2+X2L
- Here, XL is the inductive reactance, which is given by:
XL=ωL=2πfL
- Where f is the frequency of the applied source.
3. Analyze the Effect of Increasing Frequency:
- When the frequency f increases, the inductive reactance XL also increases because XL is directly proportional to frequency:
XL∝f
- As a result, the total impedance Z of the circuit increases:
Z=√R2+(2πfL)2
4. Relate Impedance to Power:
- The power (P) consumed in the circuit can be expressed as:
P=V2Z
- Here, V is the voltage across the circuit. Since Z is in the denominator, as Z increases, the power P decreases.
5. Conclude the Effect on Brightness:
- The brightness of the bulb is directly proportional to the power consumed. Therefore, if the power decreases due to the increase in impedance, the brightness of the bulb will also decrease.
Final Answer:
If the frequency of the applied source is increased, the brightness of the bulb will decrease.
- The circuit consists of a bulb (which represents a load) connected in series with an inductor (L) and a resistor (R). The brightness of the bulb is related to the power consumed in the circuit.
- The total impedance (Z) in the circuit can be expressed as:
Z=√R2+X2L
- Here, XL is the inductive reactance, which is given by:
XL=ωL=2πfL
- Where f is the frequency of the applied source.
- When the frequency f increases, the inductive reactance XL also increases because XL is directly proportional to frequency:
XL∝f
- As a result, the total impedance Z of the circuit increases:
Z=√R2+(2πfL)2
- The power (P) consumed in the circuit can be expressed as:
P=V2Z
- Here, V is the voltage across the circuit. Since Z is in the denominator, as Z increases, the power P decreases.
- The brightness of the bulb is directly proportional to the power consumed. Therefore, if the power decreases due to the increase in impedance, the brightness of the bulb will also decrease.
If the frequency of the applied source is increased, the brightness of the bulb will decrease.
Topper's Solved these Questions
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - A) ( Objective Type Questions ( One option is correct))
40 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section - B) (Objective Type Questions (One option is correct))
14 Videos
- ALTERNATING CURRENT BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ALTERNATING CURRENT EXERCISE - Assignment (Section-J) (Aakash Chailengers Questions)
2 Videos
- ATOMSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ATOMSEXERCISE - ASSIGNMENT SECTION J (Aakash Challengers )
5 Videos
Similar Questions
If number of turns in the coil is increased, how will brightness change ?
View SolutionConsider an ac circuit where an incandescent light bulb is in series with an inductor. If the frequency of generator is increased, what will happen to the brightness of bulb ?
View SolutionTwo similar bulbs of wattage 100W/50√2V are connected in circuit as shown when frequency of source is varies, brightness of B2 changes it is observed that at 50 Hz frequency both the bulbs have same brightness. Select correct alternative/s
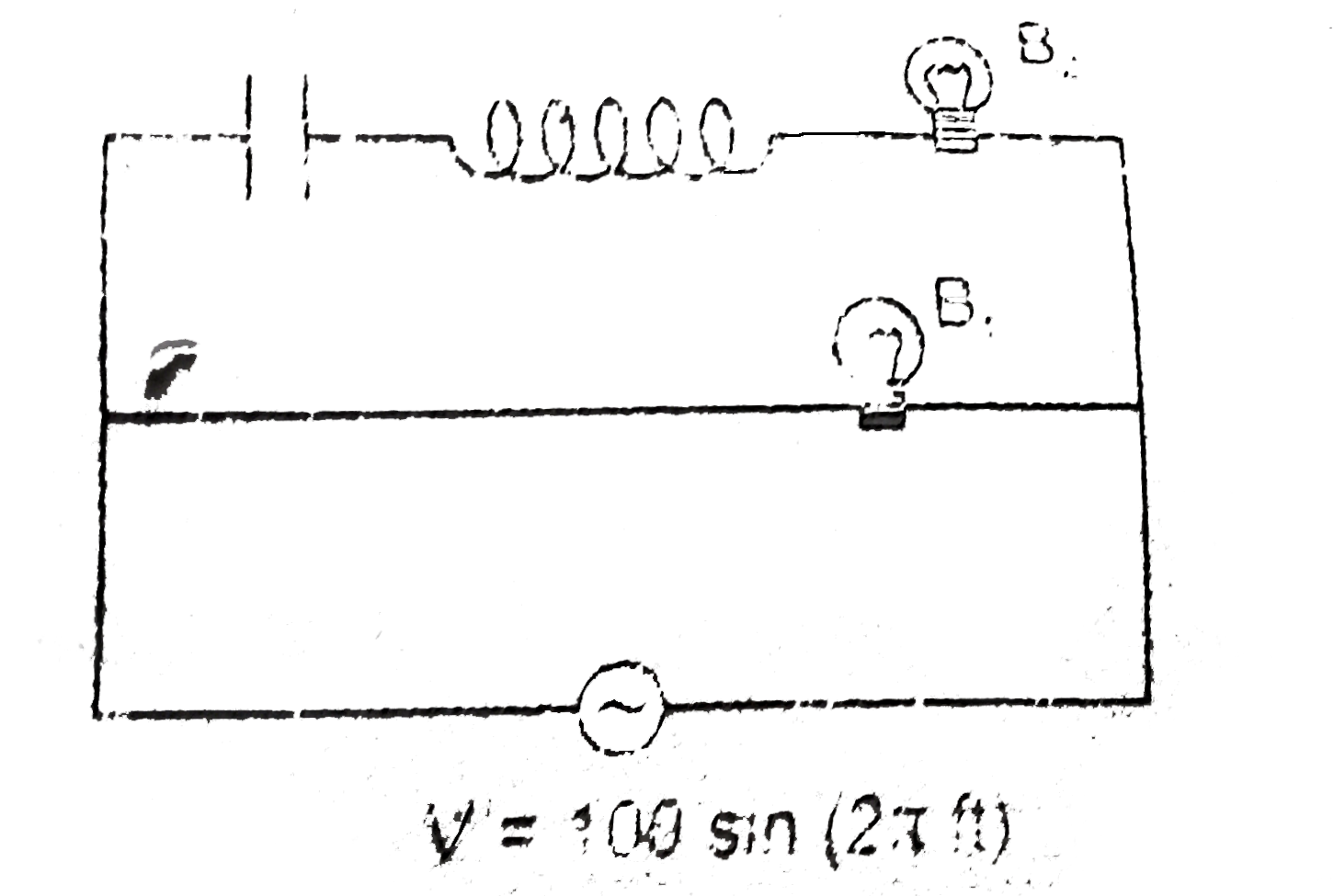
View SolutionA given LCR series circuit satisfes the condition for resonance with a given AC source. If the angular frequency of the AC source is increased by 100% then in order to establish resonance, and without changing the value of inductance, capacitance must be
View SolutionA given LCR series circuit satisfes the condition for resonance with a given AC source. If the angular frequency of the AC source is increased by 100% then in order to establish resonance, and without changing the value of inductance, capacitance must be
View SolutionFrequency of a character increase when it is
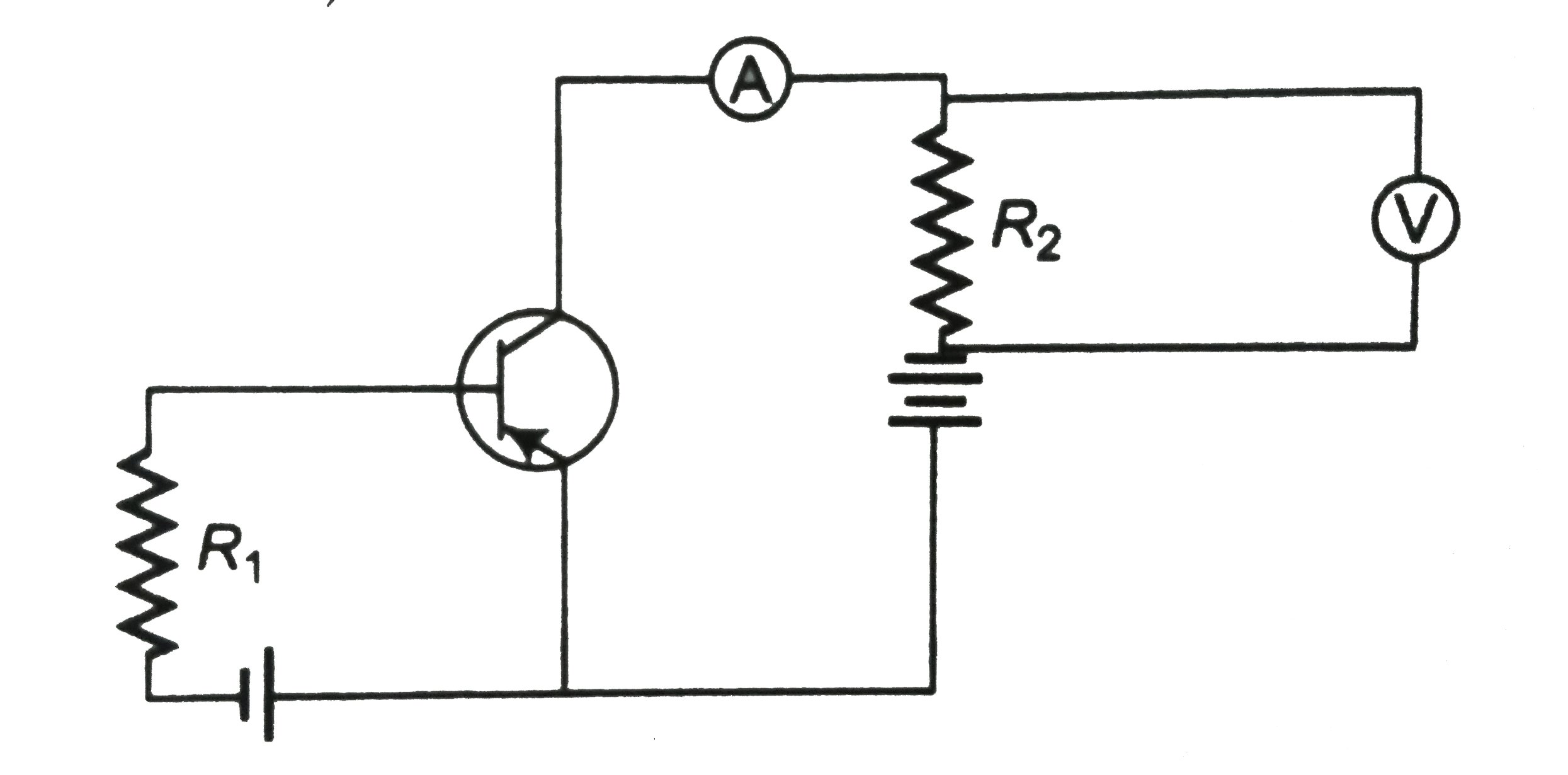
View SolutionIf the resistance R1 is increased , how will the readings of the ammeter and voltmeter change?
View SolutionAn a.c. source of angular frequency ω is fed across a resistor R and a capacitor C in series. The current registered is I. If now the frequency of the source is changed to ω/3 (but maintaining the same voltage), the current in the circuit is found to be halved. calculate the ratio of reactance to resistance at the original frequency ω.
View SolutionIncrease in frequency of urination is
View SolutionAn AC voltage source is applied across an R-C circuit. Angular frequency of the source is ω, resistance is R and capacitance is C. The current registered is I. If now the frequency of source is changed to ω2 (but maintaining the same voltage), the current in the circuit is found to be two third. calculate the ratio of reactance to resistance at the original frequency ω .
View Solution