Let z1,α,β be complex numbers of which αandβ constants and z1 varies. If z2 is given in terms of z1 by one of the following equations, it is required to find z2 corresponding to z1 then
In the given figure
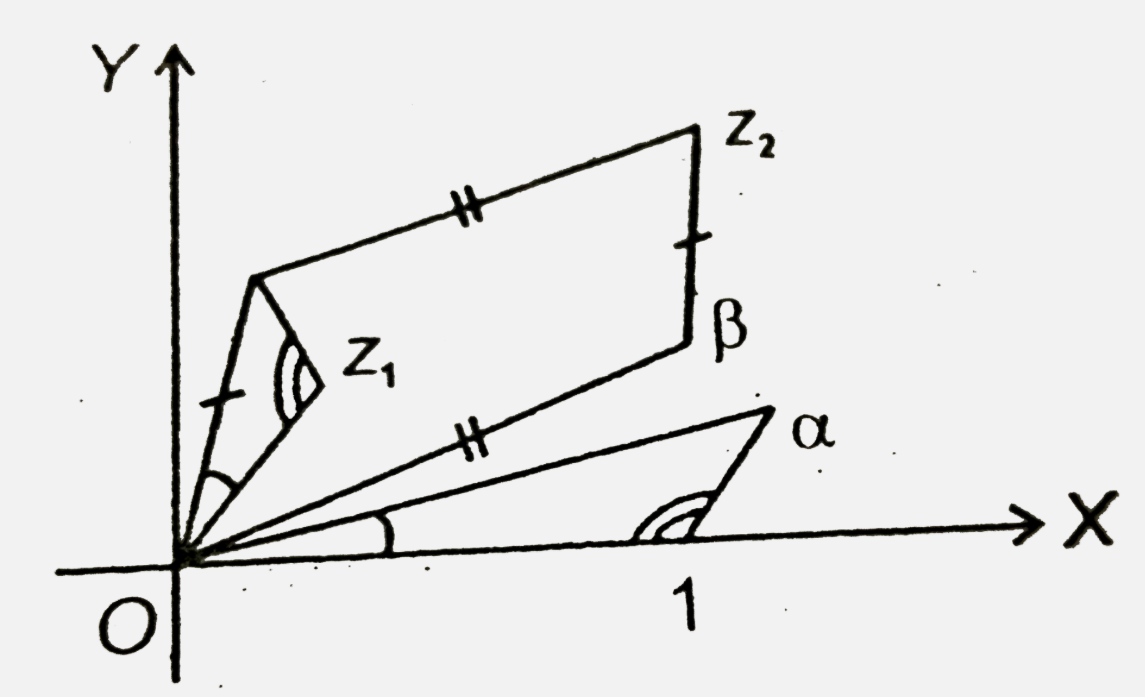
z2=αz1+β
z2=αz1β
z2=αβz1
z2=βz1
The correct Answer is:D
Step by step video & image solution for Let z_(1), alpha, beta be complex numbers of which alpha and beta constants and z_(1) varies. If z_(2) is given in terms of z_(1) by one of the following equations, it is required to find z_(2) corresponding to z_(1) then In the given figure by Maths experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Topper's Solved these Questions
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assertion -Reason Type Questions
19 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Section-F ( Matrix -Match type Question)
7 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - Assignment (Section -C) (objective Type Questions ( more thena one options are correct )
35 Videos
- BINOMIAL THEOREMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Assignment (section-J) Objective type question (Aakash Challengers Questions)
4 Videos
- CONIC SECTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - SECTION - J ( Aakash Challengers Questions )
16 Videos
Similar Questions
Let z1,α,β be complex numbers of which αandβ constants and z1 varies. If z2 is given in terms of z1 by one of the following equations, it is required to find z2 corresponding to z1 then The given figure illustrates
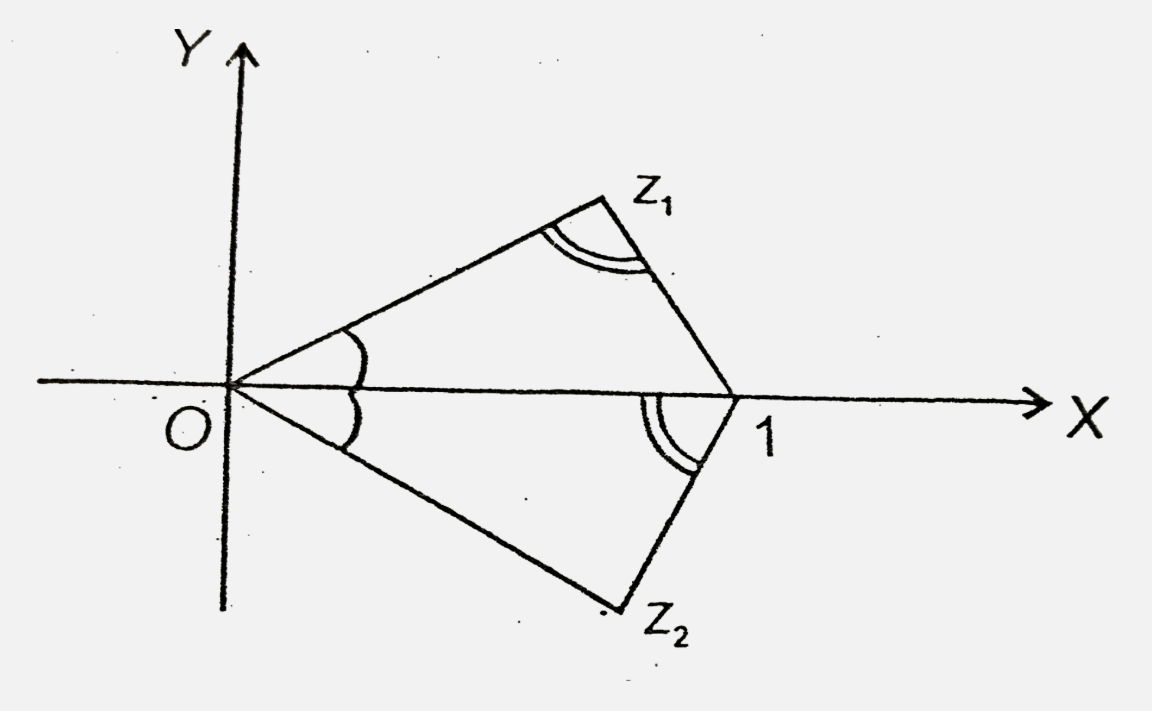
View SolutionLet z1andz2q, be two complex numbers with αandβ as their principal arguments such that α+β then principal arg(z1z2) is given by:
View SolutionLet z1,z2 be two complex numbers with |z1|=|z2|. Prove that (z1+z2)2z1z2 is real.
View SolutionLet z1,z2 be two complex numbers such that z1+z2 and z1z2 both are real, then
View SolutionLet z1,z2 be two complex numbers represented by points on the circle |z1|=andand|z2|=2 are then
View SolutionIf z1andz2 are two complex numbers such that |z1|=|z2|, then is it necessary that z1=z2
View Solutionz1thez2are two complex numbers such that|z1|=|z2|. "and"
arg (z1)+arg(z2=π, then show that z1=−¯z2.
View SolutionFor complex number z,|z−1|+|z+1|=2, then z lies on
View SolutionLet z1andz2 be two given complex numbers such that z1z2+z2z1=1and|z1|=3, then |z1−z2|2 is equal to
View SolutionLet z1andz2 be two complex numbers such that (z)1+i(z)2=0andarg(z1z2)=π. Then, find arg(z1).
View Solution