What is the last entry of any row of pascle's triangle?
The correct Answer is:1
To find the last entry of any row of Pascal's triangle, we can analyze the structure of the triangle itself. Here's a step-by-step solution:
1. Understanding Pascal's Triangle:
- Pascal's triangle is constructed by starting with a single '1' at the top (the 0th row).
- Each subsequent row is formed by adding the two numbers directly above it in the previous row.
2. Constructing the Rows:
- The 0th row is:
1
- The 1st row is:
11
- The 2nd row is:
121
- The 3rd row is:
1331
- The 4th row is:
14641
- The 5th row is:
15101051
3. Identifying the Last Entry:
- In each row, the last entry is always '1'.
- This can be observed from the construction of the triangle where each row starts and ends with '1'.
4. Conclusion:
- Therefore, the last entry of any row of Pascal's triangle is always '1'.
Final Answer:
The last entry of any row of Pascal's triangle is 1.
- Pascal's triangle is constructed by starting with a single '1' at the top (the 0th row).
- Each subsequent row is formed by adding the two numbers directly above it in the previous row.
- The 0th row is:
1
- The 1st row is:
11
- The 2nd row is:
121
- The 3rd row is:
1331
- The 4th row is:
14641
- The 5th row is:
15101051
- In each row, the last entry is always '1'.
- This can be observed from the construction of the triangle where each row starts and ends with '1'.
- Therefore, the last entry of any row of Pascal's triangle is always '1'.
The last entry of any row of Pascal's triangle is 1.
Topper's Solved these Questions
- BINOMIAL THEOREMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Assignment (section-A)
50 Videos
- BINOMIAL THEOREMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Assignment (section-B)
34 Videos
- BINOMIAL THEOREMBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - BINOMIAL THEOREMEXERCISE - Illustration
1 Videos
- APPLICATION OF INTEGRALS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - APPLICATION OF INTEGRALS EXERCISE - Assignment Section - I Aakash Challengers Questions
2 Videos
- COMPLEX NUMBERS AND QUADRATIC EQUATIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMPLEX NUMBERS AND QUADRATIC EQUATIONSEXERCISE - section-J (Aakash Challengers Qestions)
13 Videos
Similar Questions
Knowledge Check
What is the area of the triangle?
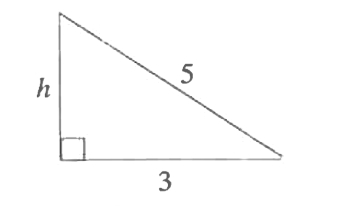 A6B7.5C8D11
A6B7.5C8D11
Prove that If the bisector of any angle of a triangle and the perpendicular bisector of its opposite side intersect, they will intersect on the circumcircle of the triangle.
View SolutionIn a flower bed there are 23 rose plants in the first row, twenty one in the second row, nineteen in the third row and so on. There are five plants in the last row. How many rows are there in the flower bed?
View SolutionIn a flower bed, therare 51 plants in the first row, 48 plants in th second row, 45 plants in the third row and so on. There are 12 plants in the last row. How many rows are there in the flower bed?
View SolutionIn a flower bed, there are 23 rose plants in the first row, 21 in the second, 19 in the third, and so on. There are 5 rose plants in the last row. How many rows are there in the flower bed?
View SolutionShow that the difference of any two sides of a triangle is less than the third side.
View SolutionProve that the straight line joining the vertex of an isosceles triangle to any point in the base is smaller than either of the equal sides of the triangle.
View SolutionShow that the difference of any two sides of a triangle is less than the third side. GIVEN : △ABC TO PROVE : (i) AC-AB < BC
View Solution
