Which of the following is not equivalent from of "if and only if " for the given statements p and q
If p then q
q if and only if p
p if and only if q
p is necesssary and suffient condition for q and vice-versa
The correct Answer is:A
To determine which of the following statements is not an equivalent form of "if and only if" (denoted as p⟺q) for the given statements p and q, we need to analyze the definitions and implications of the logical statements.
1. Understanding "If and Only If":
The statement p⟺q means that both p implies q and q implies p. This can be expressed as:
(p⟹q)∧(q⟹p)
This means that p is true if and only if q is true.
2. Analyzing the Options:
We need to evaluate the given options to see which one does not represent the same logical relationship as p⟺q.
- Option 1: p⟹q
- This is a one-way implication, meaning if p is true, then q must also be true. However, it does not account for the case where q could be true without p being true. Therefore, this is not equivalent to p⟺q.
- Option 2: q⟹p
- Similar to Option 1, this is also a one-way implication. It states that if q is true, then p must also be true. This does not capture the bidirectional nature of p⟺q.
- Option 3: p is necessary and sufficient for q
- This statement directly reflects the definition of p⟺q since it indicates that p being true guarantees q is true and vice versa. Thus, this is equivalent to p⟺q.
- Option 4: p=q or q=p
- This statement also captures the essence of p⟺q, as it indicates that p and q are equal in truth value.
3. Conclusion:
From the analysis, we find that Options 3 and 4 are equivalent to p⟺q, while Options 1 and 2 are not. However, since we are looking for the one that is not equivalent, we can conclude that:
The answer is Option 1: p⟹q.
The statement p⟺q means that both p implies q and q implies p. This can be expressed as:
(p⟹q)∧(q⟹p)
This means that p is true if and only if q is true.
We need to evaluate the given options to see which one does not represent the same logical relationship as p⟺q.
- This is a one-way implication, meaning if p is true, then q must also be true. However, it does not account for the case where q could be true without p being true. Therefore, this is not equivalent to p⟺q.
- Similar to Option 1, this is also a one-way implication. It states that if q is true, then p must also be true. This does not capture the bidirectional nature of p⟺q.
- This statement directly reflects the definition of p⟺q since it indicates that p being true guarantees q is true and vice versa. Thus, this is equivalent to p⟺q.
- This statement also captures the essence of p⟺q, as it indicates that p and q are equal in truth value.
From the analysis, we find that Options 3 and 4 are equivalent to p⟺q, while Options 1 and 2 are not. However, since we are looking for the one that is not equivalent, we can conclude that:
Topper's Solved these Questions
- MATHEMATICAL REASONINGBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATHEMATICAL REASONINGEXERCISE - Assignment (SECTION-C) (Linked Comprehension Type Questions) (Comprehension-I)
3 Videos
- MATHEMATICAL REASONINGBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATHEMATICAL REASONINGEXERCISE - Assignment (SECTION-C) (Linked Comprehension Type Questions) (Comprehension-II)
2 Videos
- MATHEMATICAL REASONINGBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATHEMATICAL REASONINGEXERCISE - Assignment (SECTION-A) (Objective type Questions (Only one answer))
50 Videos
- LIMITS AND DERIVATIVES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LIMITS AND DERIVATIVES EXERCISE - Section - j
3 Videos
- MATRICESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MATRICESEXERCISE - Assignment (Section - J) Aakash Challengers Questions
3 Videos
Similar Questions
Knowledge Check
p14q−3p−2q12
Which of the following is equivalent to the expression above, where p>1 and q>1?Ap24√pq3√qBp2√pq3√qC4√pq3√qD4√p3√q2
Which of the following is logically equivalent to ( p^q) ?
View SolutionWhich of the following is logically equivalent to ~(p→q) ?
View SolutionWhich of the following is logically equivalent to ~(~p→q)?
View SolutionWhich of the following is not true regarding the statement "p if and only if q"?
View SolutionGiven the circuit :
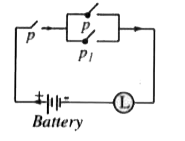
Which of the following is equivalent to the above circuit ?
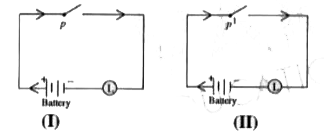
The true statement in the above is/are
View SolutionIn which of the following is equivalent cases, p⇒q is false ?
View SolutionFor the following circuit the equivalent capacitance P and Q is

View Solution
