If −1≤[2x2−3]<2, then x belongs to
−√52<x≤−1 only
≤x<√52 only
−√52lrx≤−1 or 1≤x≤√52
−1≤x≤1
The correct Answer is:C
To solve the inequality −1≤2x2−3<2, we will break it down into two parts and solve each part step by step.
Step 1: Solve the left part of the inequality
We start with the left part of the inequality:
2x2−3≥−1
Add 3 to both sides:
2x2≥2
Now, divide both sides by 2:
x2≥1
Taking the square root of both sides gives:
x≤−1orx≥1
Step 2: Solve the right part of the inequality
Now, we will solve the right part of the inequality:
2x2−3<2
Add 3 to both sides:
2x2<5
Now, divide both sides by 2:
x2<52
Taking the square root of both sides gives:
−√52<x<√52
Step 3: Combine the results
Now we need to combine the results from both parts:
1. From the left part, we have x≤−1 or x≥1.
2. From the right part, we have −√52<x<√52.
Now we will find the intersection of these two results.
- For x≤−1:
- The intersection with −√52<x gives us −√52<x≤−1.
- For x≥1:
- The intersection with x<√52 gives us 1≤x<√52.
Final Answer
Thus, the solution set is:
x∈(−√52,−1)∪(1,√52)
We start with the left part of the inequality:
2x2−3≥−1
Add 3 to both sides:
2x2≥2
Now, divide both sides by 2:
x2≥1
Taking the square root of both sides gives:
x≤−1orx≥1
Now, we will solve the right part of the inequality:
2x2−3<2
Add 3 to both sides:
2x2<5
Now, divide both sides by 2:
x2<52
Taking the square root of both sides gives:
−√52<x<√52
Now we need to combine the results from both parts:
1. From the left part, we have x≤−1 or x≥1.
2. From the right part, we have −√52<x<√52.
- The intersection with −√52<x gives us −√52<x≤−1.
- The intersection with x<√52 gives us 1≤x<√52.
Thus, the solution set is:
x∈(−√52,−1)∪(1,√52)
Topper's Solved these Questions
- RELATIONS AND FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - C) Objective Type Questions (More than one option are correct)
17 Videos
- RELATIONS AND FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - D) Linked Comprehension Type Questions
17 Videos
- RELATIONS AND FUNCTIONS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - RELATIONS AND FUNCTIONS EXERCISE - Assignment (Section - A) Objective Type Questions (one option is correct)
102 Videos
- PROBABILITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - PROBABILITYEXERCISE - ASSIGNMENT SECTION-J (aakash challengers questions)
11 Videos
- SEQUENCES AND SERIES BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - SEQUENCES AND SERIES EXERCISE - Assignment (SECTION - J) Aakash Challengers
11 Videos
Similar Questions
Knowledge Check
If −5<2x−3≤x+2,x∈R, then the solution set of x on the number line is
A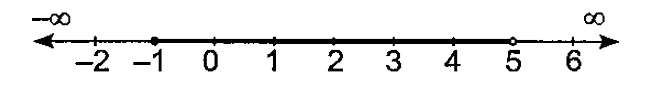 B
B C
C D
D
6≤−3(2x−4)<12
View SolutionThe value of x if 0≤|2x+3|≤3 belongs to
View SolutionIf 2sin2(x−π3)−5sin(x−π3)+2<0, then belongs to
View SolutionIf the function f(x)={x+1 if x≤1 , 2x+1 if 1<x≤2 and g(x)={x2 if −1≤x≤2, x+2if2≤x≤3 then the number of roots of the equation f(g(x))=2
View SolutionIf f(x)={2x+1.1≤x≤2x2+1.2≤x≤3, then evaluate ∫31f(x)dx.
View SolutionSolve : 6≤−3(2x−4)<12
View SolutionIf −3<x2−λx−2x2+x+1<2 for all x∈R, then the value of λ belongs to
View Solution
