Let ϕ:[0,1]→[0,1] be a continuous and one-one function. Let ϕ(0)=0,ϕ(1)=1,ϕ(12)=pandϕ(14)=q then
p>q
p<q
p = q
No comparison between p and q
The correct Answer is:A
To solve the problem, we need to analyze the properties of the function ϕ defined from the interval (0,1) to itself. Here are the steps to arrive at the conclusion regarding the relationship between p and q.
1. Understanding the Function:
We have a function ϕ:(0,1)→(0,1) which is continuous and one-to-one. This means that for every x1,x2∈(0,1), if x1<x2, then ϕ(x1)<ϕ(x2). Therefore, ϕ is a strictly increasing function.
Hint: Recall that a one-to-one function (injective) means that different inputs yield different outputs.
2. Given Values:
We know:
- ϕ(0)=0
- ϕ(1)=1
- ϕ(12)=p
- ϕ(14)=q
3. Comparing Inputs:
Since 12>14, and knowing that ϕ is strictly increasing, we can conclude:
ϕ(12)>ϕ(14)
4. Substituting Known Values:
Substituting the values we have:
p>q
5. Conclusion:
Therefore, the relationship between p and q is:
p>q
Final Answer:
The relationship between p and q is p>q.
We have a function ϕ:(0,1)→(0,1) which is continuous and one-to-one. This means that for every x1,x2∈(0,1), if x1<x2, then ϕ(x1)<ϕ(x2). Therefore, ϕ is a strictly increasing function.
We know:
- ϕ(0)=0
- ϕ(1)=1
- ϕ(12)=p
- ϕ(14)=q
Since 12>14, and knowing that ϕ is strictly increasing, we can conclude:
ϕ(12)>ϕ(14)
Substituting the values we have:
p>q
Therefore, the relationship between p and q is:
p>q
The relationship between p and q is p>q.
Topper's Solved these Questions
- RELATIONS AND FUNCTIONS Book:AAKASH INSTITUTE ENGLISHChapter:RELATIONS AND FUNCTIONS Exercise:Assignment (Section - I) Subjective Type Questions
Explore 17 Videos
- PROBABILITYBook:AAKASH INSTITUTE ENGLISHChapter:PROBABILITYExercise:ASSIGNMENT SECTION-J (aakash challengers questions)
Explore 11 Videos
- SEQUENCES AND SERIES Book:AAKASH INSTITUTE ENGLISHChapter:SEQUENCES AND SERIES Exercise:Assignment (SECTION - J) Aakash Challengers
Explore 11 Videos
Similar Questions
If ϕ(x)=ϕ'(x) and ϕ(1)=2, then ϕ(3) equals
View SolutionA continuously differentiable function ϕ(x)∈(0,π/2) satisfying y'=1+y2,y(0)=0, is
View SolutionIf ϕ(x) is a differentiable function ∀x∈Randa∈R+ such that ϕ(0)=ϕ(2a),ϕ(a)=ϕ(3a)andϕ(0)≠ϕ(a), then show that there is at least one root of equation ϕ'(x+a)=ϕ'(x)in(0,2a).
View SolutionA continuously differentiable function ϕ(x) in (0,π) satisfying y'=1+y2,y(0)=0=y(π) is
View SolutionProve that
sin2ϕ(1+cot2ϕ)=1
View SolutionLet ϕ(x,t)={x(t−1)x≤tt(x−1)t<x, where t is a continuous function of x in [0,1]. Let g(x)=∫10f(t)ϕ(x,t)dt, then g''(x)= (A) g(0)+g(1)=1 (B) g(0)=0 (C) g(1)=1 (D) g''(x)=f(x)
View SolutionLet dydx=yϕ'(x)−y2ϕ(x), where ϕ(x) is a function satisfies ϕ(1)=1,ϕ(4)=1296. If y(1) = 1 then y(4) is equal to__________
View SolutionIf ϕ(x) is a diferential real-valuted function satisfying ϕ'(x)+2ϕ(x)≤1. prove that ϕ(x)−12 is a non-incerasing function of x.
View SolutionTwo sinusoidal waves of the same frequency travel in the same direction along a string. If A1=m3.0cm,A2=4.0cm,ϕ1=0, and ϕ2=π/2rad, what is the amplitude of the resultant wave ?
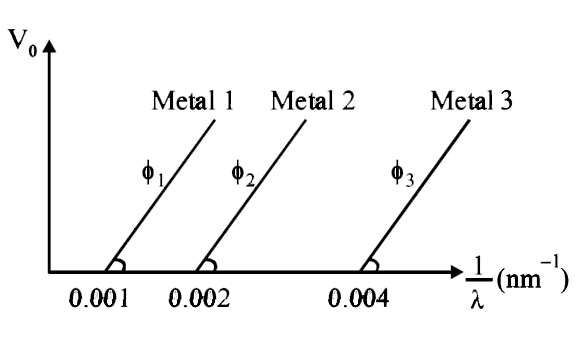
View SolutionThe graph between the stopping potential (V0)and(1λ) is shown in the figure ϕ1,ϕ2andϕ3 are work function , which of the following is /are correct
View Solution