STATEMENT -1 : f(x)=1−cos(1−cosx)x4 is continuous if f(0)=1/8
and
STATEMENT -2 : limx→0+f(x)=limx→0−f(x)=18
Statement -1 is True, Statement -2 is True, Statement -2 is a correct explantion for Statement -1
Statement -1 is True, Statement -2 is True, Statement -2 is NOT a correct explanation for Statement -1
Statement -1 is True , Statement -2 is Flase
Statement -1 is Flase , Statement - 2 is True
The correct Answer is:A
To determine the continuity of the function f(x)=1−cos(1−cosx)x4 at x=0 and to evaluate the limits as x approaches 0 from both sides, we will follow these steps:
Step 1: Evaluate f(0)
We need to define f(0) to check continuity. The statement claims that f(0)=18.
Step 2: Find the limit as x approaches 0
We need to compute:
limx→0f(x)=limx→01−cos(1−cosx)x4
Step 3: Analyze the limit
As x→0:
- cosx→1
- Therefore, 1−cosx→0
- Consequently, 1−cos(1−cosx)→1−cos(0)=0
Both the numerator and denominator approach 0, which indicates we can apply L'Hôpital's Rule or use Taylor series expansion.
Step 4: Use Taylor series expansion
Using the Taylor series expansion for cosx:
cosx≈1−x22+O(x4)
Thus,
1−cosx≈x22
Substituting this into f(x):
1−cos(1−cosx)≈1−cos(x22)
Using the Taylor expansion for cos:
cos(x22)≈1−(x2/2)22=1−x48
So,
1−cos(x22)≈x48
Step 5: Substitute back into the limit
Now substituting back into the limit:
f(x)≈x48x4=18
Thus,
limx→0f(x)=18
Step 6: Check continuity
Since:
limx→0f(x)=18=f(0)
we conclude that f(x) is continuous at x=0.
Conclusion
Both statements are correct:
- Statement 1: f(x) is continuous at x=0 if f(0)=18.
- Statement 2: limx→0+f(x)=limx→0−f(x)=18.
We need to define f(0) to check continuity. The statement claims that f(0)=18.
We need to compute:
limx→0f(x)=limx→01−cos(1−cosx)x4
As x→0:
- cosx→1
- Therefore, 1−cosx→0
- Consequently, 1−cos(1−cosx)→1−cos(0)=0
Using the Taylor series expansion for cosx:
cosx≈1−x22+O(x4)
Thus,
1−cosx≈x22
Substituting this into f(x):
1−cos(1−cosx)≈1−cos(x22)
Using the Taylor expansion for cos:
cos(x22)≈1−(x2/2)22=1−x48
So,
1−cos(x22)≈x48
Now substituting back into the limit:
f(x)≈x48x4=18
Thus,
limx→0f(x)=18
Since:
limx→0f(x)=18=f(0)
we conclude that f(x) is continuous at x=0.
Both statements are correct:
- Statement 1: f(x) is continuous at x=0 if f(0)=18.
- Statement 2: limx→0+f(x)=limx→0−f(x)=18.
Topper's Solved these Questions
- CONTINUITY AND DIFFERENTIABILITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section - F
3 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section -G
3 Videos
- CONTINUITY AND DIFFERENTIABILITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CONTINUITY AND DIFFERENTIABILITYEXERCISE - Section - D
6 Videos
- CONIC SECTIONSBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CONIC SECTIONSEXERCISE - SECTION - J ( Aakash Challengers Questions )
16 Videos
- DETERMINANTS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DETERMINANTS EXERCISE - SECTION - J
12 Videos
Similar Questions
For the function f(x)=2. Find limx→1f(x)
View SolutionIf f is an even function, then prove that limx→0−f(x)=limx→0+f(x)
View SolutionStatement-1 : limx→01−cosxx(2x−1)=12log2e.
Statement : limx→0sinxx=1, limx→0ax−1x=loga,a>0
View SolutionCalculate limx→0f(x), where f(x)=1x2 for x>0
View SolutionThe graph of y = f(x) is as shown in the following figure.
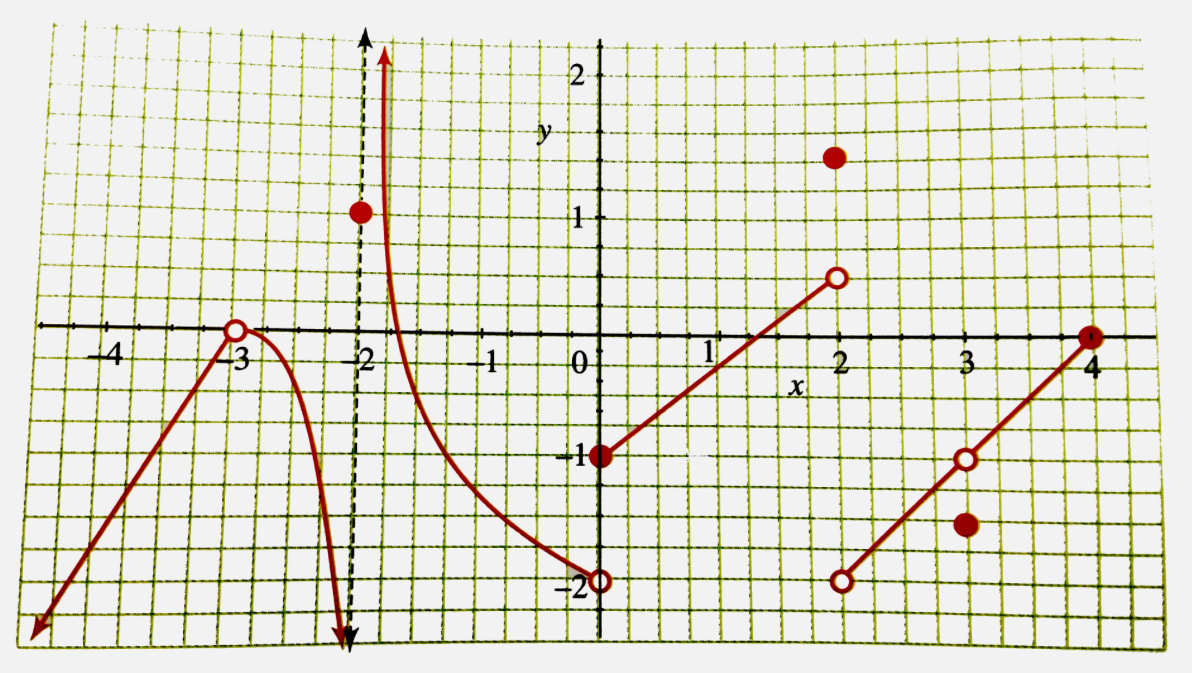
Find the following values
(i)f(−3) (ii)f(−2) (iii)f(0)
(iv)f(2) (v)f(3) (vi)limx→−3f(x)
(vii)limx→0f(x) (viii)limx→2f(x) (ix)limx→3f(x)
(x)limx→2−f(x) (ξ)limx→−2+f(x) (xii)limx→0−f(x)
(x iii) limx→0+f(x)
View SolutionIt is given that f(x) = ax+bx+1,Limx→0f(x)andLimx→∞f(x)=1 Prove that fx(-2) = 0 .
View SolutionThe value of f(0), so that the function
f(x)=1−cos(1−cosx)x4 is continuous everywhere is
View SolutionThe value of f(0), so that the function
f(x)=1−cos(1−cosx)x4 is continuous everywhere is
View SolutionLet f(x) is a function continuous for all x∈R except at x = 0 such that f'(x)<0,∀x∈(−∞,0)andf'(x)>0,∀x∈(0,∞). If limx→0+f(x)=3,limx→0−f(x)=4andf(0)=5, then the image of the point (0, 1) about the line, y.limx→0f(cos3x−cos2x)=x.limx→0f(sin2x−sin3x), is
View SolutionSTATEMENT -1 : The function f:[−1,1]→[0,π],f(x)=cos−1x is not one-one. and STATEMENT -2 :The function f:(−∞,∞)→[−1,1],f(x)=cosx is not one-one.
View Solution
