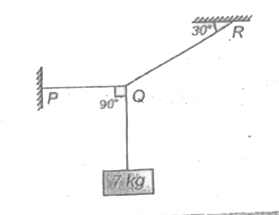
Find the tension in the horizontal string PQ and the string QR in the given figure [ Take g =10m/s2]
![Find the tension in the horizontal string PQ and the string QR in the given figure [ Take g = 10 m//s^(2)]](https://d10lpgp6xz60nq.cloudfront.net/physics_images/AAK_T1_PHY_C03_SLV_014_Q01.png)
We may take the components and redraw it as
(##∀KT1PHYC03SLV014_S01.png width=80%><br>Fromfigure,we≥t<br> T_(1) sin 30^(@) = 70 N<br>and T_(2) = T_(1) cos 30^(@)<br> :. T_(1) = 140 N<br>and T_(2) = 140 xx sqrt(3)/2 = 70 sqrt(3) N
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Illustration
7 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - TRY YOURSELF
69 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Find the tension in the horizontal string PQ and the string QR in the given figure. [Take g=10m/s2]
View SolutionFind the tension in the strings AC and BC shown in figure.

View SolutionA block of mass 1 kg and density 0.8g/cm3 is held stationary with the help of a string as shown in figure. The tank is accelerating vertically upwards with an acceleration a =1.0m/s2. Find

(a) the tension in the string,
(b) if the string is now cut find the acceleration of block.
(Take g=10m/s2 and density of water =103kg/m3).
View SolutionThe tension T in the string shown in figure is

View SolutionConsider the situation shown in figure. The block B moves on a frictionless surface ,while the coefficient of friction between A and the surface on which it moves is 0.2. Find the acceleration with which the masses move and also the tension in the strings. (Takeg=10m/s2).

View SolutionA uniform rod of length 1m and mass 2kg is suspended. Calculate tension T (in N) in the string at the instant when the right string snaps (g=10m/s2).

View SolutionA ball of mass 0.6kg attached to a light inextensible string rotates in a vertical circle of radius 0.75m such that it has speed of 5ms−1 when the string is horizontal. Tension in the string when it is horizontal on other side is (g=10ms−2).
View SolutionOne end of a string of length 1 m is tied to a body of mass 0.5 kg. It is whirled in a vertical circle with angular velocity 4 rad s−1. Find the tension in the string when the body is at the lower most point of its motion. (take, g = 10 ms−1)
View SolutionCalculate the tension in the string shown in the figure. All the surfaces are frictionless. (Take g=10/ms−1)

View SolutionIn the system shown in figure all surface are smooth, string in massless and inextensible. Find:

(a) acceleration of the system
(b) tensionin the string and
(c ) tension in the spring if force constant of spring is k = 50 N/m (Take g = 10 m/s2)
View Solution
