Two blocks of masses 4 kg and 2√3 kg are placed on fixed smooth wedge . They are connected by means of a massless inextensible string that passes over the pulley/ The angle of inclinations are 30∘and60∘ as shown in figure . Select the correct alternative ( g = 10 m/s2)
The blocks will remain at rest
The magnitude of acceleration of blocks is 52+√3m/s2
The tension in the string is 20(3+√32+√3) N
The tension in the sring is 20√3 N
The correct Answer is:B, C
To solve the problem, we need to analyze the forces acting on both blocks and apply Newton's second law of motion. Let's break down the steps:
Step 1: Identify the Forces Acting on Each Block
1. Block 1 (4 kg on 30° incline):
- Weight (W1) = m1 * g = 4 kg * 10 m/s² = 40 N
- The component of weight acting down the incline (F1) = W1 * sin(30°) = 40 N * (1/2) = 20 N
2. Block 2 (2√3 kg on 60° incline):
- Weight (W2) = m2 * g = 2√3 kg * 10 m/s² = 20√3 N
- The component of weight acting down the incline (F2) = W2 * sin(60°) = 20√3 N * (√3/2) = 30 N
Step 2: Set Up the Equation of Motion
- The net force acting on the system can be expressed as:
Fnet=F2−F1
Substituting the values:
Fnet=30N−20N=10N
Step 3: Calculate the Total Mass of the System
- The total mass (M) of the system is the sum of the masses of both blocks:
M=m1+m2=4kg+2√3kg
Step 4: Calculate the Acceleration of the System
- Using Newton's second law (F = ma), we can find the acceleration (a):
a=FnetM=10N4kg+2√3kg
Step 5: Calculate the Tension in the String
- For Block 1 (4 kg):
T=W1−F1+m1∗a
Substituting the values:
T=40N−20N+4kg∗a
- For Block 2 (2√3 kg):
T=F2−W2+m2∗a
Substituting the values:
T=30N−20√3N+2√3kg∗a
Step 6: Solve for Tension and Acceleration
- Equate the two expressions for tension (T) and solve for acceleration (a) and then substitute back to find T.
Final Result
- After calculations, we find the tension in the string and the acceleration of the blocks.
1. Block 1 (4 kg on 30° incline):
- Weight (W1) = m1 * g = 4 kg * 10 m/s² = 40 N
- The component of weight acting down the incline (F1) = W1 * sin(30°) = 40 N * (1/2) = 20 N
- Weight (W2) = m2 * g = 2√3 kg * 10 m/s² = 20√3 N
- The component of weight acting down the incline (F2) = W2 * sin(60°) = 20√3 N * (√3/2) = 30 N
- The net force acting on the system can be expressed as:
Fnet=F2−F1
Substituting the values:
Fnet=30N−20N=10N
- The total mass (M) of the system is the sum of the masses of both blocks:
M=m1+m2=4kg+2√3kg
- Using Newton's second law (F = ma), we can find the acceleration (a):
a=FnetM=10N4kg+2√3kg
- For Block 1 (4 kg):
T=W1−F1+m1∗a
Substituting the values:
T=40N−20N+4kg∗a
- For Block 2 (2√3 kg):
T=F2−W2+m2∗a
Substituting the values:
T=30N−20√3N+2√3kg∗a
- Equate the two expressions for tension (T) and solve for acceleration (a) and then substitute back to find T.
- After calculations, we find the tension in the string and the acceleration of the blocks.
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -D) Linked Comprehension Type Question
1 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -D) Linked Comprehension Type Question (Comprehension -I)
2 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -B) objective type questions (one option is correct)
59 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Two masses 6 kg and 4 kg are connected by massless flexible and inextensible string passing over massless and frictionless pulley.The acceleration of centre of mass is (g=10ms^2)
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly

View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
Two masses of 3 kg and 4 kg are connected at the two ends of a light inextensible string that passes over a frictionless pulley. Find the acceleration of the masses and the tension in the string, when the masses are released.
View SolutionTwo bodies of masses 4 kg and 6 kg are tied to the ends of a massless string. The string passes over a frictionless pulley. The acceleration of the system is :
View SolutionTwo unequal masses of 1kg and 2kg are connected by an inextensible light string passing over a smooth pulley as shown in figure. A force F=20N is applied on 1kg block find the acceleration of either block (g=10m/s2).

View SolutionTwo blocks of masses 6kg and 4kg are attached to the two ends of a massless string passing over a smooth fixed pulley. if the system is released, the acceleration of the centre of mass of the system will be
View SolutionTwo block of masses 2kg and 4kg are released from rest over a smooth inclined place of inclination 30∘ as shown in figure what is the normal force between the two blocks?

View SolutionBlock A of mass m and block B of mass 2m are placed on a fixed traingular wedge by means of a massless inextensible string and a frictionless pulley as shown in figure The wedge is inclined at 45∘to the horizontal on both sides .The coefficient of friction between blocks A and the wedge is 2/3 and that between block B and is released from rest find the following
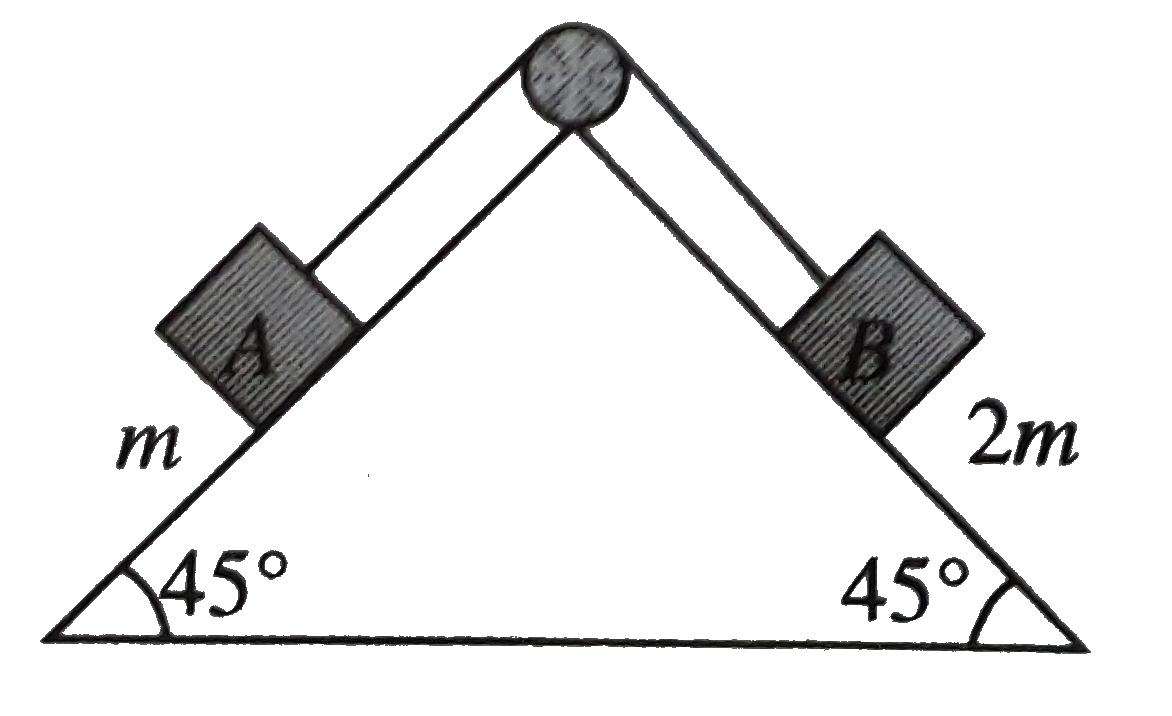
The tension in the string is
View SolutionBlock A of mass m and block B of mass 2m are placed on a fixed traingular wedge by means of a massless inextensible string and a frictionless pulley as shown in figure The wedge is inclined at 45∘to the horizontal on both sides .The coefficient of friction between blocks A and the wedge is 2/3 and that between block B and is released from rest find the following
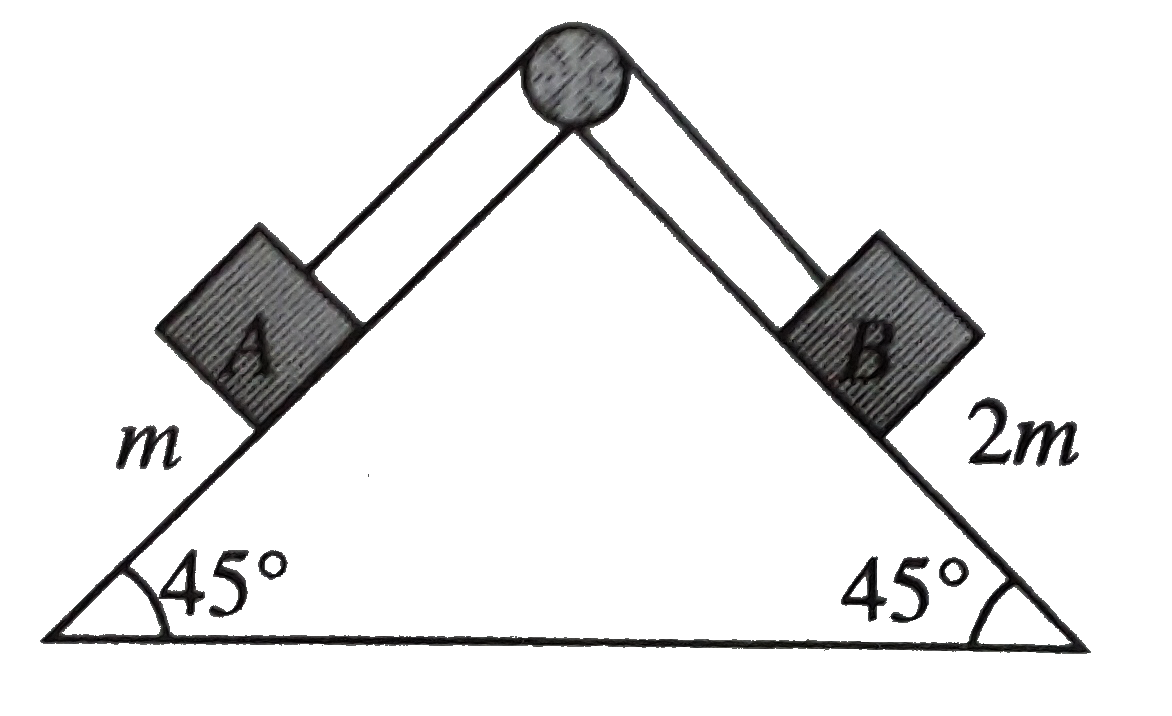
The magnitude and direction of the force of friction acting on A are
View Solution
