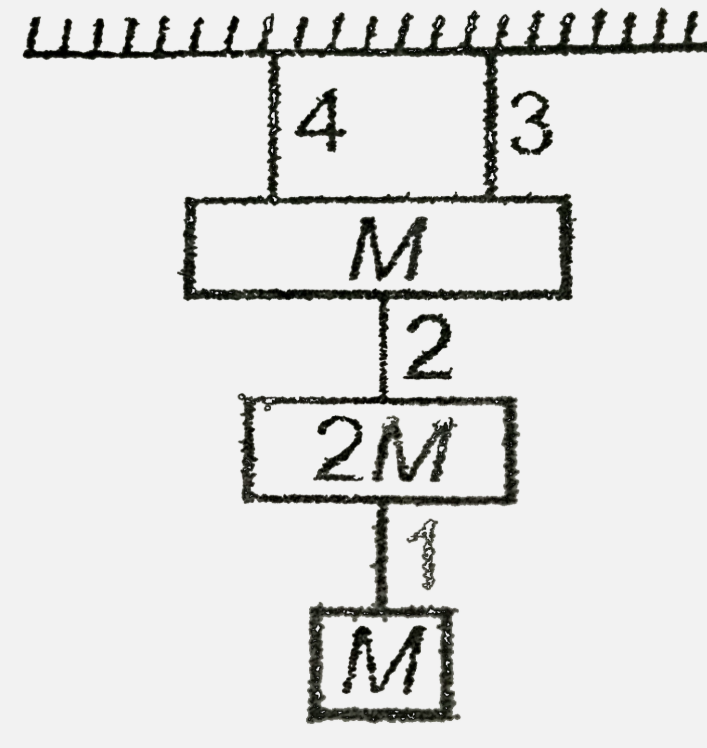
STATEMENT-1 : Tension at every point in a string with mass at every cross section must be unequal , if the string is accelerating .
and
STATEMENT - 2 : If we draw free body diagram for any section of the string , net external force acting on the string has to be equal to product of its mass ( which is non- zero ) and its acceleration .
Statement -1 True, Statement -2 is True , Statement - 2 is a correct explanation for Statement -2
Statement -1 is True , Statement -2 is True , Statement -2 is NOT a correct explanation for statement -2
Statement -1 is true, Statement -2 is False
Statement - 1 is False , Statement - 2 is True
The correct Answer is:D
To solve the given problem, we need to analyze both statements and determine their validity based on the principles of physics, particularly Newton's laws of motion.
1. Understanding Statement 1:
- Statement 1 claims that "Tension at every point in a string with mass at every cross section must be unequal if the string is accelerating."
- To evaluate this, we consider a string that is accelerating. If we take a small segment of the string, the tension at one end of the segment (let's call it T1) and the tension at the other end (T2) can be analyzed.
2. Analyzing the Forces:
- For a small element of the string with mass dm, the net force acting on it can be expressed as:
T1−T2=dm⋅a
- Here, a is the acceleration of the string, and dm is the mass of the small segment.
3. Conclusion for Statement 1:
- From the equation T1−T2=dm⋅a, it is clear that if the string is accelerating, the tensions T1 and T2 must indeed be different (i.e., T1≠T2). Therefore, Statement 1 is true.
4. Understanding Statement 2:
- Statement 2 states that "If we draw a free body diagram for any section of the string, the net external force acting on the string has to be equal to the product of its mass (which is non-zero) and its acceleration."
- This is a direct application of Newton’s second law of motion, which states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration.
5. Applying Newton's Second Law:
- For the entire string, if we consider the total mass M and the acceleration a, the net force F acting on the string can be expressed as:
F=M⋅a
- This is consistent with the free body diagram analysis where the net force is the difference in tension at the ends of the string.
6. Conclusion for Statement 2:
- Since the statement correctly reflects Newton's second law, Statement 2 is true.
Final Evaluation:
- Statement 1: True (Tension must be unequal in an accelerating string).
- Statement 2: True (Net force equals mass times acceleration).
- Statement 1 claims that "Tension at every point in a string with mass at every cross section must be unequal if the string is accelerating."
- To evaluate this, we consider a string that is accelerating. If we take a small segment of the string, the tension at one end of the segment (let's call it T1) and the tension at the other end (T2) can be analyzed.
- For a small element of the string with mass dm, the net force acting on it can be expressed as:
T1−T2=dm⋅a
- Here, a is the acceleration of the string, and dm is the mass of the small segment.
- From the equation T1−T2=dm⋅a, it is clear that if the string is accelerating, the tensions T1 and T2 must indeed be different (i.e., T1≠T2). Therefore, Statement 1 is true.
- Statement 2 states that "If we draw a free body diagram for any section of the string, the net external force acting on the string has to be equal to the product of its mass (which is non-zero) and its acceleration."
- This is a direct application of Newton’s second law of motion, which states that the net force acting on an object is equal to the mass of the object multiplied by its acceleration.
- For the entire string, if we consider the total mass M and the acceleration a, the net force F acting on the string can be expressed as:
F=M⋅a
- This is consistent with the free body diagram analysis where the net force is the difference in tension at the ends of the string.
- Since the statement correctly reflects Newton's second law, Statement 2 is true.
- Statement 1: True (Tension must be unequal in an accelerating string).
- Statement 2: True (Net force equals mass times acceleration).
Topper's Solved these Questions
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -F ) Matrix - Match Type Questions
4 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -G ) Integer Answer Type Questions
7 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - ASSIGNMENT ( SECTION -D) Linked Comprehension Type Question (Comprehension -IV) (Choose the correct answer :)
3 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - EXERCISE (ASSIGNMENT) SECTION - D Assertion - Reason Type Questions
10 Videos
- MAGNETISM AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - MAGNETISM AND MATTER EXERCISE - ASSIGNMENT (SECTION D)
26 Videos
Similar Questions
Knowledge Check
Force of friction and tension in a string are
AGravitational forcesBElectromagnetic forcesCNuclear forcesDWeal forces
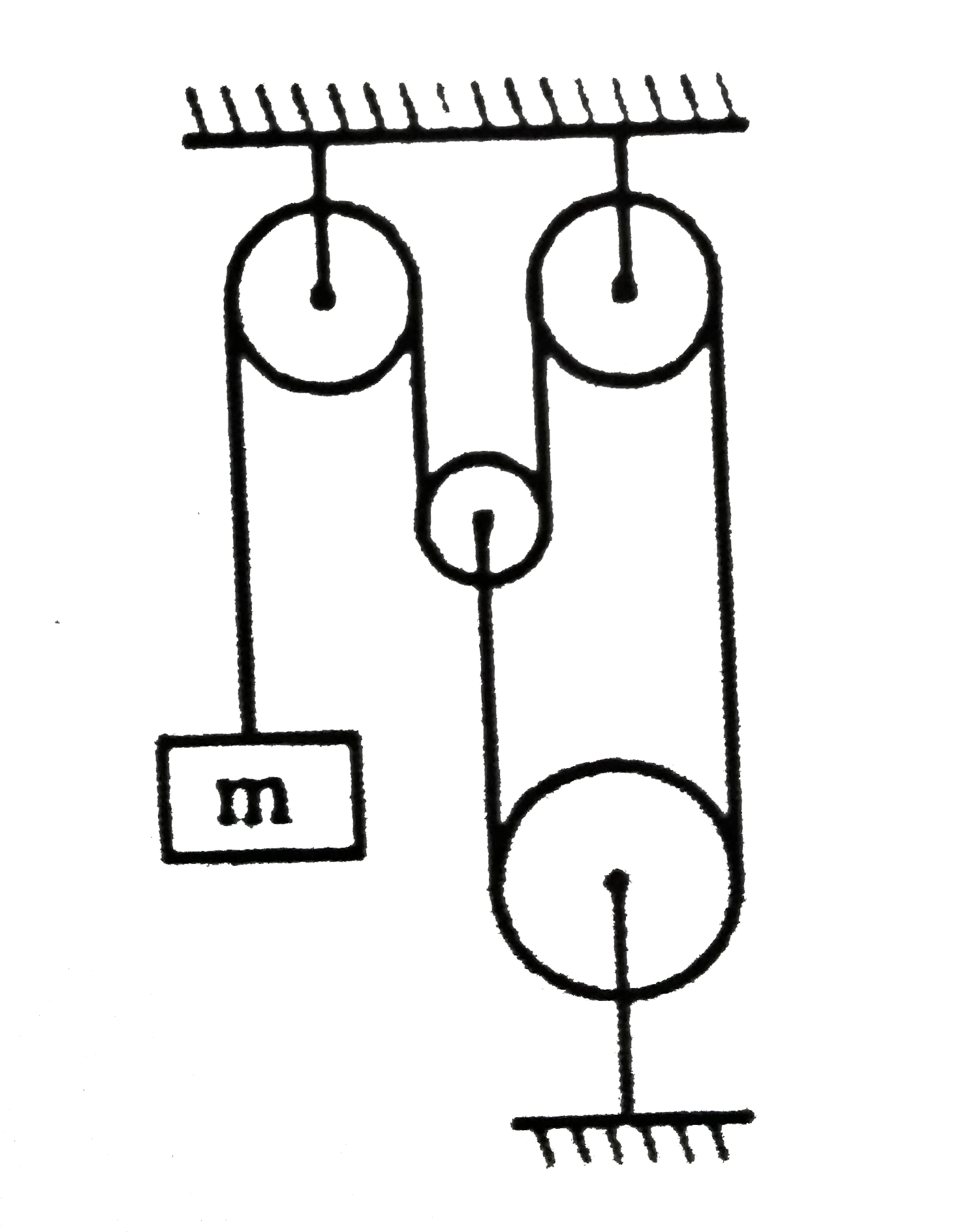
If the string & all the pulleys are ideal, acceleration of mass m is :-
View SolutionThe mass of the part of the string below A in figure is m. Find the tension of the string at the lower end and at A.
View SolutionA string of 7 m length has a mass of 0.035 kg. If tension in the string is 60.5 N, then speed of a wave on the string is :
View SolutionThe block of mass m is at rest. Find the tension in the string A .

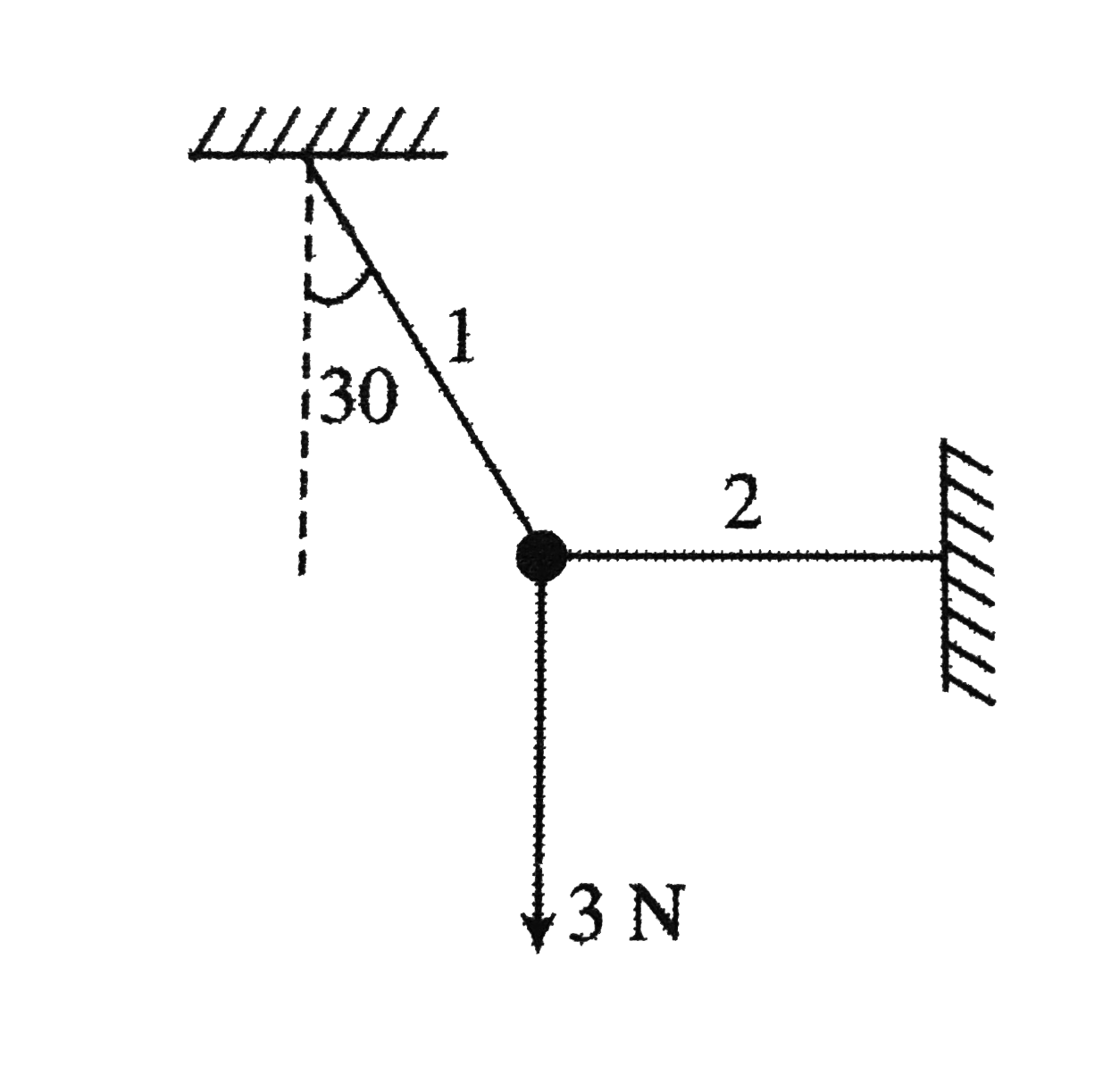
View SolutionA bob of weight 3N is in equilibrium under the action of two string 1 and 2 (figure) . Find the tension forces in the string.
View SolutionA string of 7m length has a mass of 0.035kg. If tension in the string is 60.N, then speed of a wave on the string is
View SolutionA disc of mass M has a light, thin string wrapped several times around its circumference. The free end of string is attaced to the ceiling and the disc is released from rest. Find the acceleration of the disc and the tension in the string.
View Solution