If 3 moles of gas is mixed with 2 moles of helium gas, then calculate equivalent molar mass of the gas and adiabatic exponent of the mixture?
To solve the problem of finding the equivalent molar mass and the adiabatic exponent (gamma) of a mixture of gases, we will follow these steps:
Step 1: Identify the given data
- Moles of H2 (diatomic gas): n1=3 moles
- Molar mass of H2: m1=2 g/mol
- Moles of helium (monatomic gas): n2=2 moles
- Molar mass of helium: m2=4 g/mol
Step 2: Calculate the equivalent molar mass of the gas mixture
The formula for equivalent molar mass M of the mixture is given by:
M=n1m1+n2m2n1+n2
Substituting the values:
M=(3moles×2g/mol)+(2moles×4g/mol)3+2
Calculating the numerator:
=(6+8)5=145=2.8g/mol
Step 3: Calculate the degree of freedom for each gas
- For H2 (diatomic gas), the degree of freedom f1=5.
- For helium (monatomic gas), the degree of freedom f2=3.
Step 4: Calculate the degree of freedom of the mixture
The formula for the degree of freedom f of the mixture is given by:
f=n1f1+n2f2n1+n2
Substituting the values:
f=(3×5)+(2×3)3+2
Calculating the numerator:
=(15+6)5=215=4.2
Step 5: Calculate the adiabatic exponent γ of the mixture
The formula for the adiabatic exponent γ is given by:
γ=1+2f
Substituting the value of f:
γ=1+2215=1+1021=3121≈1.476
Final Answers
- Equivalent molar mass of the gas mixture: 2.8g/mol
- Adiabatic exponent γ of the mixture: 1.476
- Moles of H2 (diatomic gas): n1=3 moles
- Molar mass of H2: m1=2 g/mol
- Moles of helium (monatomic gas): n2=2 moles
- Molar mass of helium: m2=4 g/mol
The formula for equivalent molar mass M of the mixture is given by:
- For H2 (diatomic gas), the degree of freedom f1=5.
- For helium (monatomic gas), the degree of freedom f2=3.
The formula for the degree of freedom f of the mixture is given by:
The formula for the adiabatic exponent γ is given by:
- Equivalent molar mass of the gas mixture: 2.8g/mol
- Adiabatic exponent γ of the mixture: 1.476
Topper's Solved these Questions
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Try Yourself
43 Videos
- KINETIC THEORYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - KINETIC THEORYEXERCISE - Assignment (Section-A) Objective type questions (One option is correct)
49 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
- LAWS OF MOTIONBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - LAWS OF MOTIONEXERCISE - Assignment (SECTION-D) (Assertion-Reason Type Questions)
15 Videos
Similar Questions
Knowledge Check
Two moles of gas A at 27∘C mixed with a 3 moles of gas at 37∘C. If both are monatomic ideal gases, what will be the temperature of the mixture ?
A66∘CB11∘CC22∘CD33∘C1 mole of a gas with γ=7/5 is mixed with 1 mole of a gas with γ=5/3, then the value of γ for the resulting mixture is
A75B25C32D127
In an isobaric process (λ is adiabatic exponent of the gas)
View SolutionWhen one mole of monoatomic gas is mixed with one mole of triatomic gas, then the equivalent value of γ for the mixture will be (vibration mode neglected)
View Solutionn1 mole of a monoatomic gas is mixed with n2 mole of a diatomic gas. (Assume gases are ideal). If for the mixture adiabatic contant is found to be 1.5, then n1:n2 is :
View SolutionWhen 1 mole of monatomic gas is mixed 1 mole of diatomic gas, then find Cp,Cv,γandf for mixture of the gas.
View SolutionFive moles of helium are mixed with two moles of hydrogen to form a mixture. Take molar mass of helium M1=4g and that of hydrogen M2=2g
If the internal energy of He sample is 100J and that of the hydrogen sample is 200J , then the internal energy of the mixture is
View SolutionNo. of moles of H2 gas evolved when one mole of the following compound reacts with sodium.
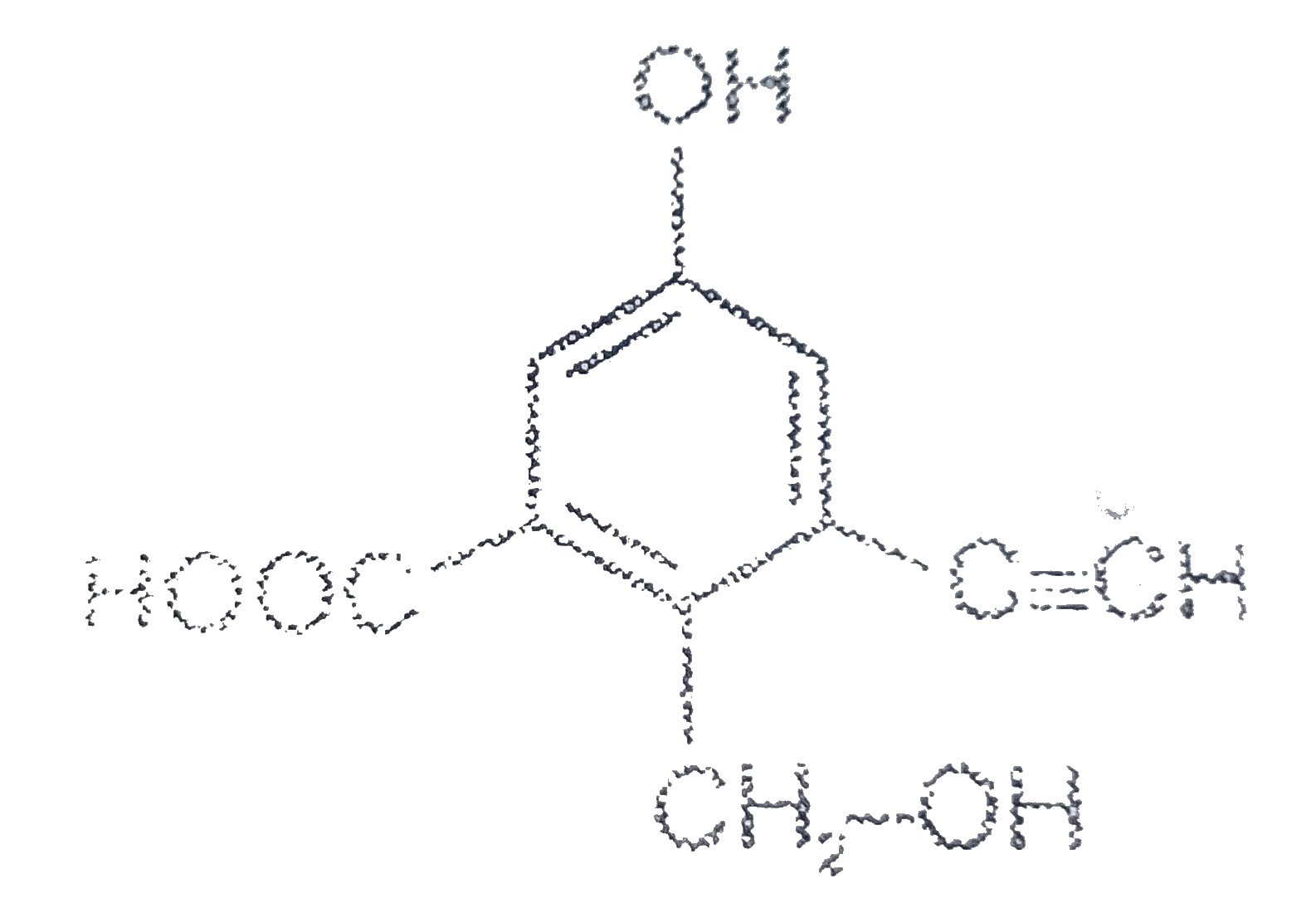
View Solution
