The capacitance of an isolated conducting sphere of radius R is proportional to
4πε0r
2πε0r
πε0r
8πε0r
The correct Answer is:1
To find the capacitance of an isolated conducting sphere of radius R, we can follow these steps:
Step 1: Understand the relationship between charge, potential, and capacitance
The capacitance C of a conductor is defined as the ratio of the charge Q on the conductor to the potential V at its surface:
C=QV
Step 2: Determine the potential V at the surface of the sphere
For a conducting sphere with charge Q and radius R, the potential V at the surface is given by the formula:
V=kQR
where k is a constant. In electrostatics, k is often represented as k=14πϵ0.
Step 3: Substitute the expression for V into the capacitance formula
Substituting the expression for V into the capacitance formula, we get:
C=QV=QkQR=Rk
Step 4: Substitute the value of k
Now, substituting k=14πϵ0 into the equation for capacitance:
C=R14πϵ0=4πϵ0R
Step 5: Determine the proportionality
From the final expression C=4πϵ0R, we can see that the capacitance C is directly proportional to the radius R of the sphere.
Conclusion
Thus, the capacitance of an isolated conducting sphere of radius R is proportional to R.
Final Answer
The capacitance C of an isolated conducting sphere is proportional to R.
---
The capacitance C of a conductor is defined as the ratio of the charge Q on the conductor to the potential V at its surface:
C=QV
For a conducting sphere with charge Q and radius R, the potential V at the surface is given by the formula:
V=kQR
where k is a constant. In electrostatics, k is often represented as k=14πϵ0.
Substituting the expression for V into the capacitance formula, we get:
C=QV=QkQR=Rk
Now, substituting k=14πϵ0 into the equation for capacitance:
C=R14πϵ0=4πϵ0R
From the final expression C=4πϵ0R, we can see that the capacitance C is directly proportional to the radius R of the sphere.
Thus, the capacitance of an isolated conducting sphere of radius R is proportional to R.
The capacitance C of an isolated conducting sphere is proportional to R.
Topper's Solved these Questions
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B (OBJECTIVE TYPE QUESTIONS (ONLY ONE ANSWER) )
1 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - SECTION-B(OBJECTIVE TYPE QUESTIONS(ONLY ONE ANSWER) )
29 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROSTATIC POTENTIAL AND CAPACITANCE EXERCISE - ASSIGNMENT SECTION - D
9 Videos
- ELECTROMAGNETIC WAVESBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - ELECTROMAGNETIC WAVESEXERCISE - ASSIGNMENT SECTION - D Assertion-Reason Type Questions
25 Videos
- GRAVITATION BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - GRAVITATION EXERCISE - ASSIGNMENT SECTION - D (ASSERTION-REASON TYPE QUESTIONS)
15 Videos
Similar Questions
Draw a plot showing variation of electric field with distance from the centre of a solid conducting sphere of radius R, having of + Q on its surface.
View SolutionA conducting sphere of radius r has a charge . Then .
View SolutionThe net charge given to an isolated conducting solid sphere :
View SolutionThe capacitance of a metallic sphere is 1μF, if its radius is
View SolutionA point charge q is placed at some distance d away from the centre of a grounded conducting sphere of radius r, as shown in the figure. The charge that flows the earth to the sphere is
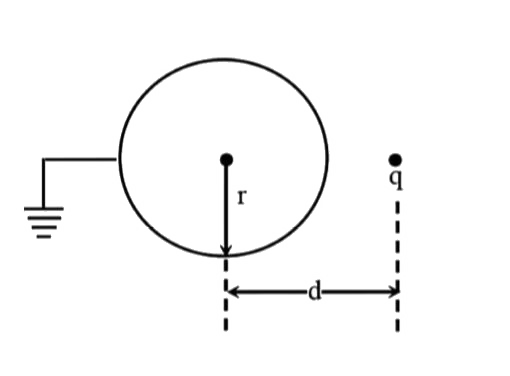
View Solution
consider a neutral conducting sphere of radius a with a spherical cavity of radius b. A charged conducting sphere of radius c is placed in cavity . Centre of this sphere coincide with centre of cavity charge on the inner sphere is q total self energy of this arrangement is:
View SolutionA point charge q is placed at a distance of r from cebtre of an uncharged conducting sphere of rad R(<r). The potential at any point on the sphere is
View SolutionWe have an isolated conducting spherical shell of radius 10cm. Some positive charge is given to it so that the resulting electric field has a maximum intensity of 1.8×106NC−1. The same amount of negative charge is given to another isolated conducting spherical shell of radius 20cm. Now, the first shell is placed inside the second so that both are concentric as shown in (Fig. 3.154).
 .
.
If both the spheres are connected by a conducting wire, then.
View SolutionA conducting sphere of radius R and carrying a charge Q is joined to an uncharged conducting sphere of radius 2R. The charge flowing between them will be
View SolutionTwo conducting spheres of radius R and 3R carry charges Q and −2Q. Between these spheres a neutral conducting sphere of radius 2R is connected. The separation between the sphere is considerably large Charge flows through conducting wire due to potential difference.

The final charge on initially neutral conducting sphere is :
View Solution
