The ratio of magnitude of current density and magnitude of electric field inside the conductor is
Independent of temperature
Independent of dimension of conductor
Independent of material of conductor
All of these
The correct Answer is:2
To solve the question regarding the ratio of the magnitude of current density (J) to the magnitude of electric field (E) inside a conductor, we can follow these steps:
1. Understanding Ohm's Law:
Ohm's law states that the voltage (V) across a conductor is proportional to the current (I) flowing through it, given by the equation:
V=I×R
where R is the resistance of the conductor.
2. Relating Current to Current Density:
The current density (J) is defined as the current (I) per unit area (A) through which the current flows:
J=IA
3. Expressing Resistance in Terms of Resistivity:
The resistance (R) of a conductor can be expressed in terms of its resistivity (ρ), length (L), and cross-sectional area (A):
R=ρLA
4. Substituting Resistance in Ohm's Law:
By substituting the expression for R into the equation for Ohm's law, we get:
V=I×ρLA
5. Rearranging to Find Current Density:
Dividing both sides by A, we can express the current density (J):
J=IA=VρLA=V⋅AρL
6. Simplifying the Expression:
Since VL is the electric field (E), we can rewrite the expression for J:
J=1ρ⋅E
7. Finding the Ratio of Current Density to Electric Field:
To find the ratio of the magnitude of current density (J) to the magnitude of electric field (E), we rearrange the equation:
JE=1ρ
8. Relating to Conductivity:
The reciprocal of resistivity (ρ) is conductivity (σ):
σ=1ρ
Therefore, we can express the ratio as:
JE=σ
Final Answer:
The ratio of the magnitude of current density (J) to the magnitude of electric field (E) inside the conductor is:
JE=σ
Ohm's law states that the voltage (V) across a conductor is proportional to the current (I) flowing through it, given by the equation:
V=I×R
where R is the resistance of the conductor.
The current density (J) is defined as the current (I) per unit area (A) through which the current flows:
J=IA
The resistance (R) of a conductor can be expressed in terms of its resistivity (ρ), length (L), and cross-sectional area (A):
R=ρLA
By substituting the expression for R into the equation for Ohm's law, we get:
V=I×ρLA
Dividing both sides by A, we can express the current density (J):
J=IA=VρLA=V⋅AρL
Since VL is the electric field (E), we can rewrite the expression for J:
J=1ρ⋅E
To find the ratio of the magnitude of current density (J) to the magnitude of electric field (E), we rearrange the equation:
JE=1ρ
The reciprocal of resistivity (ρ) is conductivity (σ):
σ=1ρ
Therefore, we can express the ratio as:
JE=σ
The ratio of the magnitude of current density (J) to the magnitude of electric field (E) inside the conductor is:
JE=σ
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-B(OBJECTIVE TYPE QUESTION ))
44 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-C(OBJECTIVE TYPE QUESTION ))
13 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - Try Yourself
34 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
Assertion:A point charge q is placed near an arbitrary shaped solid conductor as shown in figures.The potential difference between the points A and B within the conductor remain same irrespective of the magnitude of charge q
Reason: The electric field inside a solid conductor is zero under electrostatic conditions
View SolutionThe order of magnitude of the density of nuclear matter is=
View SolutionAn electric dipole of length 10cm having charges ±6×10−3C, placed at 30∘ with respect to a uniform electric field experiences a torque of magnitude 6√3N−m. Calculate (i) magnitude of electric field (ii) the potential energy of dipole.
View SolutionIf →j and →E are current density and electric field inside a current carrying conductor at an instant then →j.→E is
(1) Positive (2) Negative
(3) Zero (4) May be positive or negative
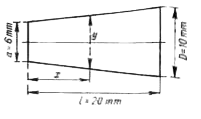
View SolutionA current of 100 A flows in a conical copper with dimensions as shown in Fig 26.8. Find the current density and electric field intensity at the end faces of the conductor
View SolutionThe ratio of current density and electric field is called (A) resistivity (B) conductivity (C) Drift velocity (D) Mobility
View SolutionWhy should electrostatic field be zero inside a conductor ?
View SolutionWhat is current density? Write the vector equation connecting current density J with electric field intensity E for an ohmic conductor.
View SolutionIf →j and →E are current density and electric field respectively inside a current carrying conductor , then correct relation is
View SolutionA nonconducting sphere with a cavity has volume charge density ρ. O1andO2 represent the two centres as shown. The electric fields inside the cavity is E0. Now, an equal and opposite charge is given uniformly to the sphere on its outer surface. The magnitude of electric field inside the cavity becomes

View Solution
