Electric current is passing through a solid conductor PQ from P to Q. The electric current densities at p and Q are in the ratio.
1:2
2:1
1:4
4:1
The correct Answer is:C
To solve the problem of finding the ratio of electric current densities at points P and Q in a solid conductor, we can follow these steps:
1. Understand the Concept of Current Density:
Current density (J) is defined as the amount of electric current (I) flowing per unit area (A) of the conductor. Mathematically, it is given by:
J=IA
2. Identify the Cross-Sectional Area:
For a cylindrical conductor, the cross-sectional area (A) can be calculated using the formula for the area of a circle:
A=πr2
where r is the radius of the conductor.
3. Define Current Densities at Points P and Q:
- Let the current density at point P be JP and at point Q be JQ.
- The current density at point P can be expressed as:
JP=IAP=Iπr2P
- The current density at point Q can be expressed as:
JQ=IAQ=Iπr2Q
4. Set Up the Ratio of Current Densities:
To find the ratio of current densities at points P and Q, we can write:
JPJQ=Iπr2PIπr2Q=r2Qr2P
Here, the current (I) and the constant (π) cancel out.
5. Assume a Relationship Between Radii:
If we assume that the radius at point P is half of that at point Q, i.e., rP=12rQ, we can substitute this into our ratio:
JPJQ=r2Q(12rQ)2=r2Q14r2Q=4
6. Final Ratio of Current Densities:
Thus, we can conclude that:
JPJQ=14
Therefore, the ratio of current densities at points P and Q is:
JP:JQ=1:4
Conclusion:
The ratio of electric current densities at points P and Q is 1:4.
Current density (J) is defined as the amount of electric current (I) flowing per unit area (A) of the conductor. Mathematically, it is given by:
J=IA
For a cylindrical conductor, the cross-sectional area (A) can be calculated using the formula for the area of a circle:
A=πr2
where r is the radius of the conductor.
- Let the current density at point P be JP and at point Q be JQ.
- The current density at point P can be expressed as:
JP=IAP=Iπr2P
- The current density at point Q can be expressed as:
JQ=IAQ=Iπr2Q
To find the ratio of current densities at points P and Q, we can write:
JPJQ=Iπr2PIπr2Q=r2Qr2P
Here, the current (I) and the constant (π) cancel out.
If we assume that the radius at point P is half of that at point Q, i.e., rP=12rQ, we can substitute this into our ratio:
JPJQ=r2Q(12rQ)2=r2Q14r2Q=4
Thus, we can conclude that:
JPJQ=14
Therefore, the ratio of current densities at points P and Q is:
JP:JQ=1:4
The ratio of electric current densities at points P and Q is 1:4.
Topper's Solved these Questions
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-C(OBJECTIVE TYPE QUESTION ))
13 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT SECTION-D( LINKED COMPREHENSION TYPE QUESTIONS)
3 Videos
- CURRENT ELECTRICITYBOOK - AAKASH INSTITUTE ENGLISHCHAPTER - CURRENT ELECTRICITYEXERCISE - ASSIGNMENT(SECTION-A(OBJECTIVE TYPE QUESTIONS))
69 Videos
- COMMUNICATION SYSTEMS BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - COMMUNICATION SYSTEMS EXERCISE - ASSIGNMENT SECTION D (Assertion-Reason)
10 Videos
- DUAL NATURE OF RADIATION AND MATTER BOOK - AAKASH INSTITUTE ENGLISHCHAPTER - DUAL NATURE OF RADIATION AND MATTER EXERCISE - ASSIGNMENT (SECTION-D)
10 Videos
Similar Questions
When no current is passed through a conductor,
View SolutionA steady electric current is flowing through a cylindrical conductor. Then,
View SolutionThe electric current drawn from cell is
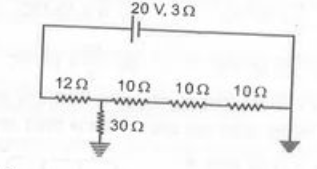
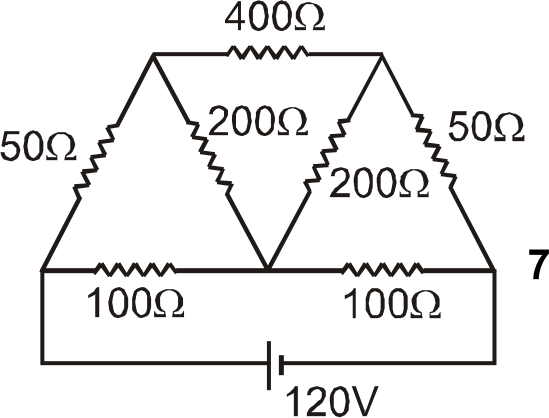
View SolutionElectric current through 400Ω resistor is :
View SolutionWhen electric current is passed through an ionic hydride in molten state:
View SolutionWhen electric current is passed through an ionic hydride in molten state:
View SolutionElectric current is passing unfiormly through a solid cylinderical wire of radius R. The current I passing through circular cross-section of radius r measured from the axis of the cylinder (r<R) varies as shown in
View SolutionWhen a steady current passes through a cylindrical conductor, is there an electric field inside the conductor?
View SolutionWhen a steady current passes through a cylindrical conductor, is there an electric field inside the conductor?
View SolutionWhen electric current is passed through water, it undergoes a …………….. Reaction.
View Solution
