An electromagneti wave propagationg through vacuum is given B=B0sin(kx−ω) . Which of the following is/are independent of frequency?
k
ωk
kω
ω
The correct Answer is:B
To solve the problem, we need to analyze the given electromagnetic wave equation and determine which quantities are independent of frequency.
Given:
The electromagnetic wave is represented as:
B=B0sin(kx−ω)
Where:
- B0 is the amplitude of the magnetic field.
- k is the wave number.
- ω is the angular frequency.
1. Identify the Wave Number k:
The wave number k is defined as:
k=2πλ
where λ is the wavelength. The wavelength is related to the frequency f by:
λ=cf
where c is the speed of light. Substituting for λ:
k=2πfc
This shows that k is directly proportional to the frequency f. Thus, k is dependent on frequency.
2. Identify the Ratio ωk:
The angular frequency ω is given by:
ω=2πf
Therefore, the ratio ωk can be calculated as follows:
ωk=2πf2πfc=c
The speed of light c is a constant and does not depend on frequency. Thus, ωk is independent of frequency.
3. Identify the Product k⋅ω:
The product k⋅ω can be expressed as:
k⋅ω=(2πfc)⋅(2πf)=(2π)2f2c
This expression clearly shows that k⋅ω is dependent on f2 and thus is dependent on frequency.
4. Identify ω:
Since ω=2πf, it is directly proportional to frequency f. Therefore, ω is dependent on frequency.
Conclusion:
From the analysis:
- Option 1: k - Dependent on frequency
- Option 2: ωk - Independent of frequency (Correct option)
- Option 3: k⋅ω - Dependent on frequency
- Option 4: ω - Dependent on frequency
Thus, the only quantity that is independent of frequency is:
Option 2: ωk.
The electromagnetic wave is represented as:
B=B0sin(kx−ω)
- B0 is the amplitude of the magnetic field.
- k is the wave number.
- ω is the angular frequency.
The wave number k is defined as:
k=2πλ
where λ is the wavelength. The wavelength is related to the frequency f by:
λ=cf
where c is the speed of light. Substituting for λ:
k=2πfc
This shows that k is directly proportional to the frequency f. Thus, k is dependent on frequency.
The angular frequency ω is given by:
ω=2πf
Therefore, the ratio ωk can be calculated as follows:
ωk=2πf2πfc=c
The speed of light c is a constant and does not depend on frequency. Thus, ωk is independent of frequency.
The product k⋅ω can be expressed as:
k⋅ω=(2πfc)⋅(2πf)=(2π)2f2c
This expression clearly shows that k⋅ω is dependent on f2 and thus is dependent on frequency.
Since ω=2πf, it is directly proportional to frequency f. Therefore, ω is dependent on frequency.
From the analysis:
- Option 1: k - Dependent on frequency
- Option 2: ωk - Independent of frequency (Correct option)
- Option 3: k⋅ω - Dependent on frequency
- Option 4: ω - Dependent on frequency
Option 2: ωk.
Topper's Solved these Questions
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT (SECTION-B) OBJECTIVE TYPE QUESTIONS (ONE OPTION IS CORRECT)
Explore 15 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:ASSIGNMENT (SECTION-C) (LINKED COMPREHENSION TYPE QUESTIONS)
Explore 3 Videos
- ELECTROMAGNETIC WAVESBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC WAVESExercise:TRY YOURSELF
Explore 22 Videos
- ELECTROMAGNETIC INDUCTIONBook:AAKASH INSTITUTE ENGLISHChapter:ELECTROMAGNETIC INDUCTIONExercise:ASSIGNMENT(SECTION -D) Assertion-Reason type Question)
Explore 15 Videos
- ELECTROSTATIC POTENTIAL AND CAPACITANCE Book:AAKASH INSTITUTE ENGLISHChapter:ELECTROSTATIC POTENTIAL AND CAPACITANCE Exercise:ASSIGNMENT SECTION - D
Explore 9 Videos
Similar Questions
Knowledge Check
The electric field of an electromagnetic wave travelling through vacuum is given by the equation E=E0sin(kx−ωt) The quantity that is independent of wavelength is
AkωBkωCk2ωDω
An electromagnetic wave is propagating in vacuum along z-axis, the electric field component is given by Ex=E0sin(kz−ωt). Then magnetic components is
View Solution(A): Two sound waves of frequencies 400 Hz and 200 Hz can propagate with the same velocity through a given medium
(R): The velocity of sound is independent of frequency
View SolutionIn a electro magnetic wave the expression for electric field is given by E=50sin(ωt−kx) the permeability is given μ=4μ0 & permittivity ε0=εr, then find the average intensity delivered.
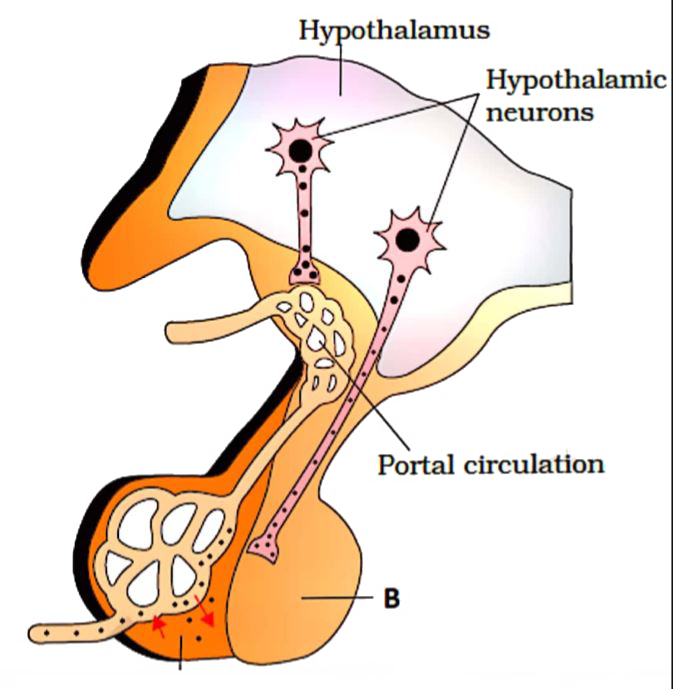
View SolutionWhich of the following hormones pass-through "route-B" in the given figure ?
View SolutionA transverse wave travelling along the positive x-axis, given by y=Asin(kx−ωt) is superposed with another wave travelling along the negative x-axis given by y=Asin(kx+ωt). The point x=0 is
View SolutionMagnetic field in a plane electromagnetic wave is given by
¯¯¯B=B0sin(kx+ωt)ˆjT
Expression for corresponding electric field will be
View SolutionMagnetic field in a plane electromagnetic wave is given by
¯¯¯B=B0sin(kx+ωt)ˆjT
Expression for corresponding electric field will be
View Solution
