The following equation gives a relation between the mass m1 kept on a surface of area A and the pressure p exerted on this area.
p=(m1+m2)xA
What must be the dimensions of the quatities x and m2?
To solve the problem, we need to analyze the given equation:
p=(m1+m2)⋅xA
where p is the pressure, m1 and m2 are masses, x is a quantity we need to find the dimensions of, and A is the area.
Step 1: Determine the dimensions of m2
Since m1 and m2 are added together in the equation, they must have the same dimensions.
- The dimension of mass m1 is given by:
(m1)=M
Thus, the dimension of m2 must also be:
(m2)=M
Step 2: Determine the dimensions of pressure p
Pressure is defined as force per unit area. The dimension of force is given by:
(F)=MLT−2
The dimension of area A is:
(A)=L2
Therefore, the dimension of pressure p is:
(p)=(F)(A)=MLT−2L2=ML−1T−2
Step 3: Analyze the right-hand side of the equation
Now we can rewrite the equation:
p=(m1+m2)⋅xA
Substituting the dimensions we have:
(p)=(m1+m2)⋅(x)(A)
Since (m1+m2)=M (as both have the same dimension), we can write:
(p)=M⋅(x)L2
Step 4: Equate the dimensions
Now we equate the dimensions of pressure:
ML−1T−2=M⋅(x)L2
To isolate (x), we multiply both sides by L2:
ML−1T−2⋅L2=M⋅(x)
This simplifies to:
ML1T−2=M⋅(x)
Now, we can cancel M from both sides (assuming M≠0):
L1T−2=(x)
Conclusion
Thus, the dimensions of x are:
(x)=LT−2
Summary of Results
- The dimensions of m2 are (m2)=M.
- The dimensions of x are (x)=LT−2.
(m1)=M
Thus, the dimension of m2 must also be:
(m2)=M
(F)=MLT−2
(A)=L2
(p)=(F)(A)=MLT−2L2=ML−1T−2
p=(m1+m2)⋅xA
(p)=(m1+m2)⋅(x)(A)
(p)=M⋅(x)L2
ML−1T−2=M⋅(x)L2
ML−1T−2⋅L2=M⋅(x)
ML1T−2=M⋅(x)
L1T−2=(x)
(x)=LT−2
- The dimensions of x are (x)=LT−2.
Similar Questions
If system is in equilibrium then find relation between m1 and m2
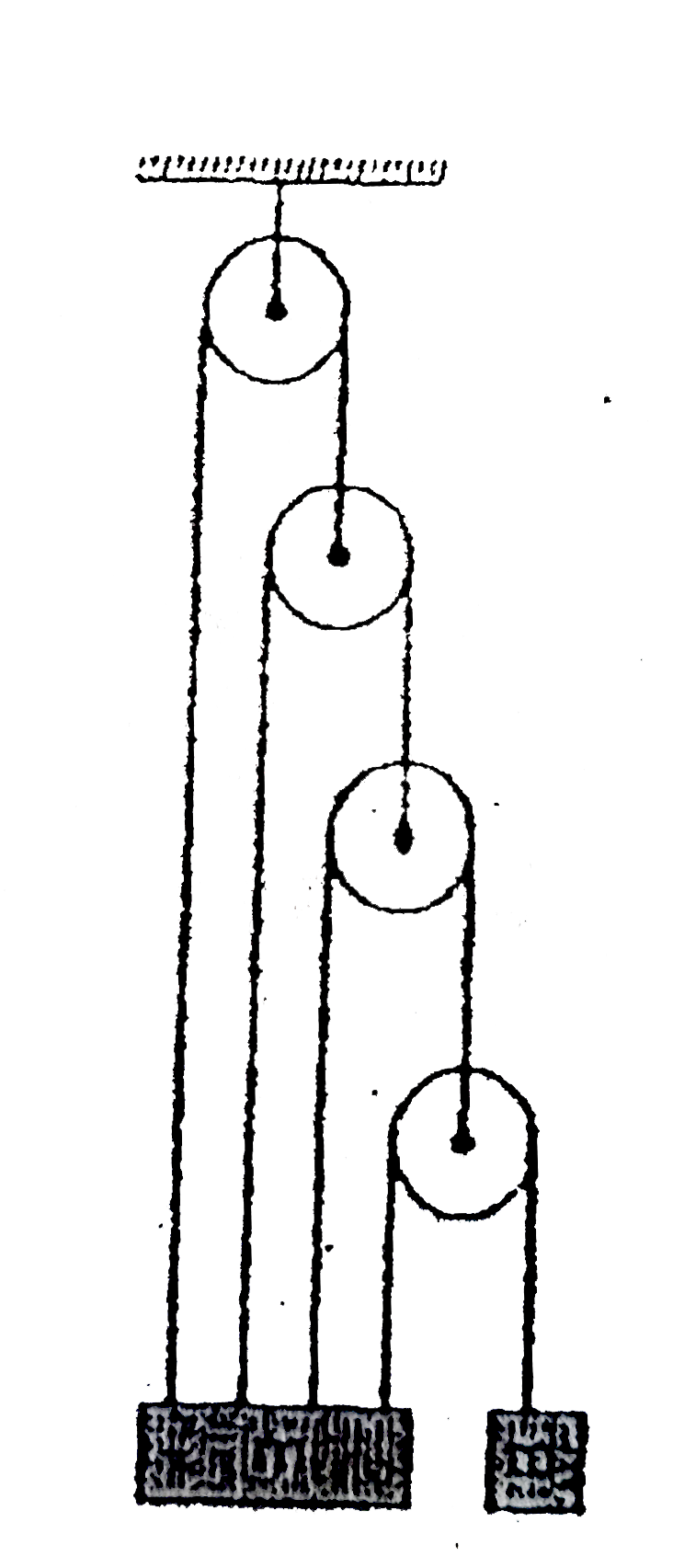
View SolutionWhen force F applied on m1 and there is no friction between m1 and surface and the coefficient of friction between m1andm2 is μ. What should be the minimum value of F so that there is on relative motion between m1andm2

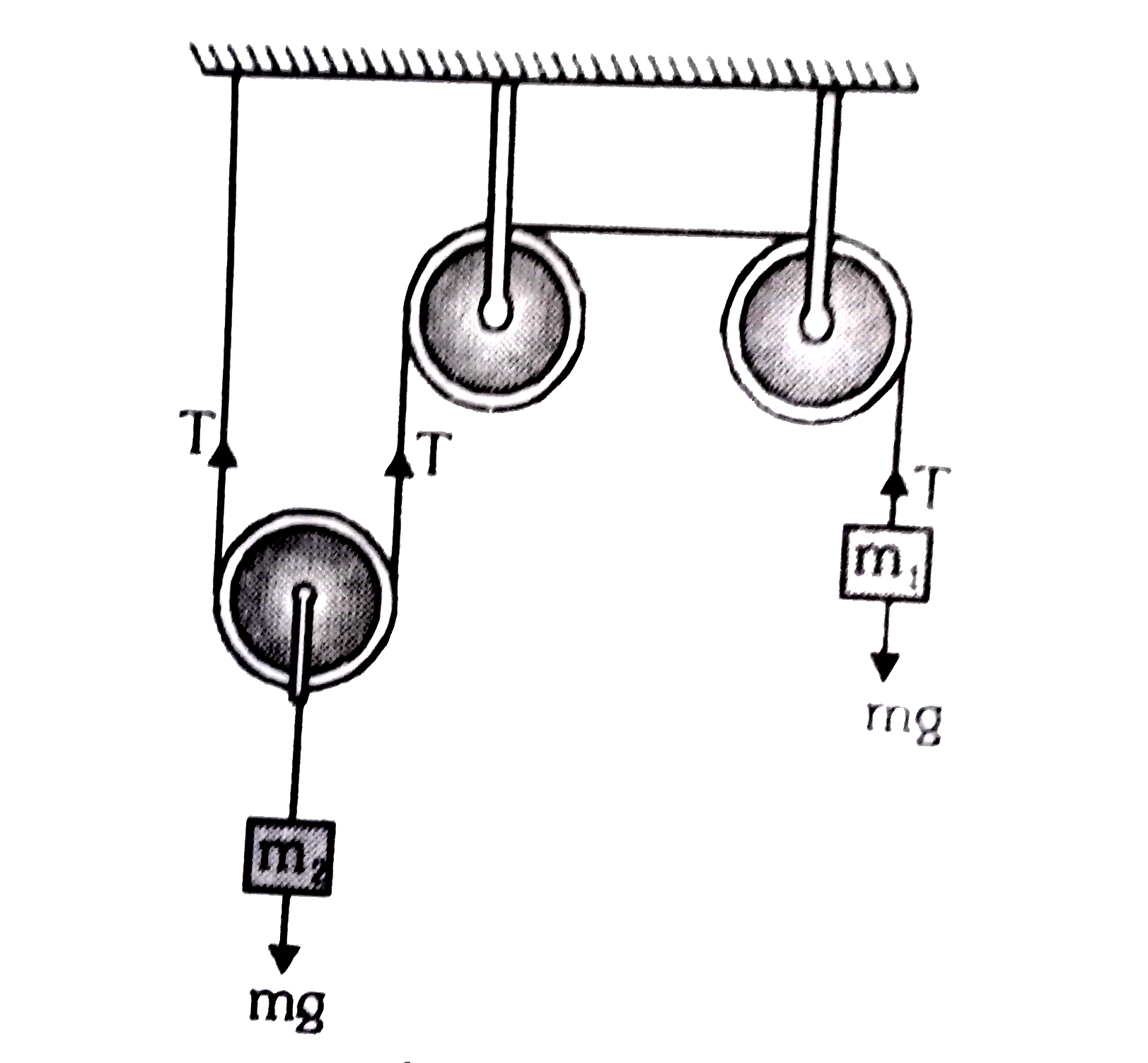
View SolutionConsider the system of masses and pulleys shown in fig. with massless string and fricitionless pulleys.
(a) Give the necessary relation between masses m1 and m2 such that system is in equilibrium and does not move.
(b) If m1=6kg and m2=8kg, calculate the magnitude and direction of the acceleration of m1.
View SolutionThe dimensions of a cuboid are in the ratio 5:3:1 and its total surface area is 414 m2. Find the dimensions.
View SolutionWhen a force of one ________ acts on an area of cross-section 1m2, the pressure exerted is said to be one ___________
View SolutionAssertion : Mass of solid floating in liquid is m1 and mass of liquid is m2. Base area is A. Then pressure at bottom is p0+(m1+m2)gA
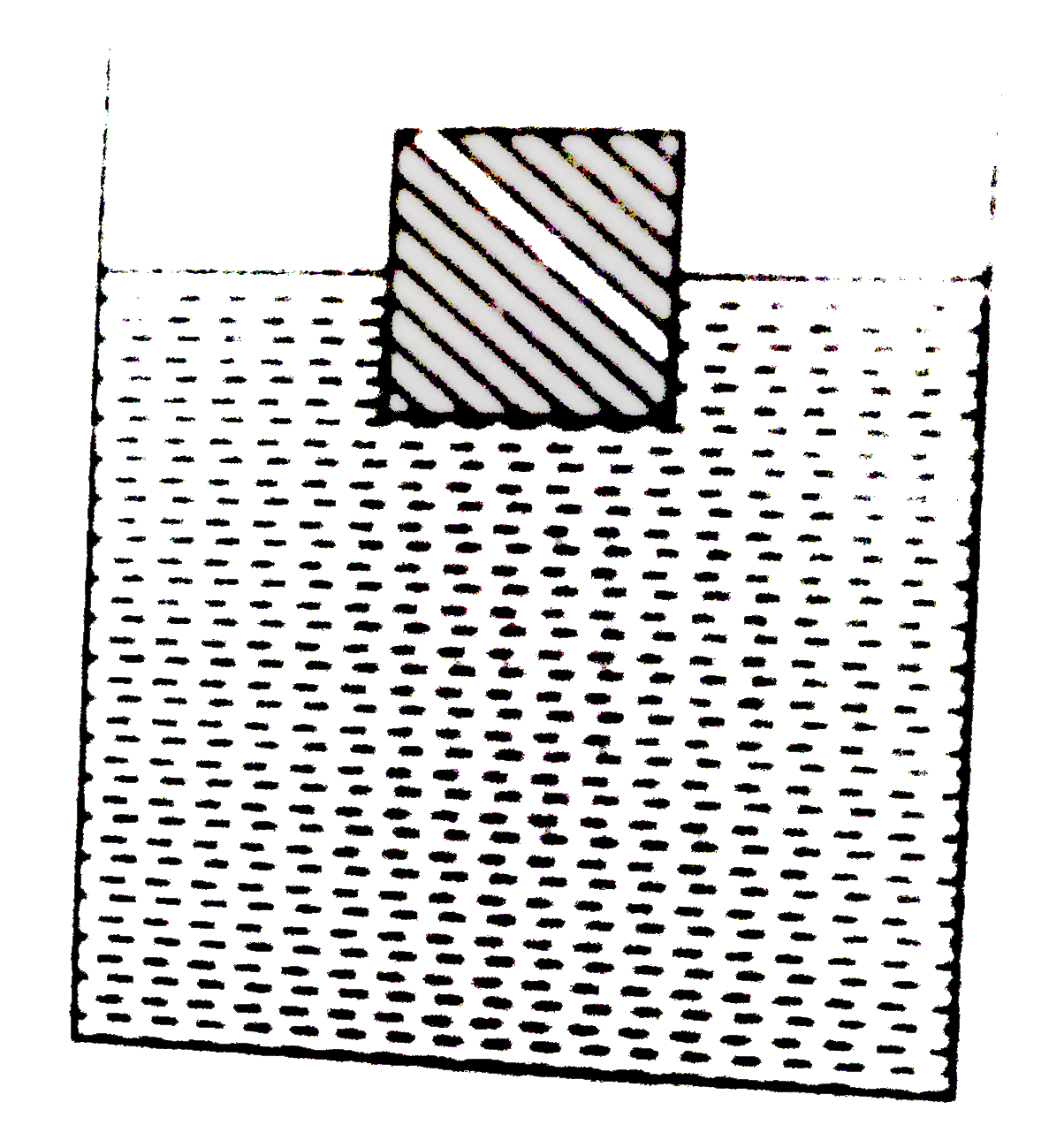
Reason : Upward force on liquid from base of vessel is pA, where p is pressure at bottom.
View SolutionThe dimensions of a cuboid are in the ratio of 1:2:3: and its total surface area is 88m2. Find the dimensions.
View SolutionThe dimensions of a cuboid are in the ratio of 1:2:3: and its total surface area is 88m2. Find the dimensions.
View SolutionWhat is the area of cross-section of a body in m2, when it exerts a force of 50 N and produces a pressure of 2000 Pa?
View SolutionA cuboid has total surface area of 40m2 and its lateral surface area is 26m2 . Find the area of its base.
View Solution
