The voltage across a lamp is (6.0 ± 0.1) V and the current flowing through it is (4.0 ±0.2)A. Find the power consumed with maximum permissible error in it.
The correct Answer is:(24.0 ± 1.6) W
Step by step video solution for The voltage across a lamp is (6.0 pm 0.1) V and the current flowing through it is (4.0 pm0.2)A. Find the power consumed with maximum permissible error in it. by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.
Updated on:21/07/2023Similar Questions
The voltage across a lamp is (6.0±0.1)V and the current passing through it is (4.0±0.2) ampare. Find the power consumed by the lamp.
View SolutionThe voltage across a lamp is 6.82 V when the current passing through it is 4.1 A. Find the power consumed to appropriate significant figures.
View SolutionThe voltage across a lamp, is 6.32V when the current passing through it is 3.4 A. Find the power consumed to appropriate significant figures.
View SolutionIn Ohm's law experiment , the potential drop acros a resistance was as V=5.0V and the current was measured as I=2.00A. Find the maximum permissible error in resistance.
View SolutionThe resistance of metal is given by V=IR, The voltage in the resistance is V=(8±0.5)V and current in the resistance is I=(2±0.2)A, the value fo resistance with its percentage error is
View SolutionThe radius of a sphere is (2.6 ± 0.1) cm The percentage error u iis volume is
View SolutionAb object covers (16.0±0.4) m distance in (4.0±0.2) s. Find out the second.
View SolutionIn ohm's law experiment potential drop across a resistance was measured as v=5.0 volt and current was measured as I=2.0amp If least count of the volmeter and ammeter are 0.1V and 0.01A respectively then find the maximum permissible error in resistance .
View SolutionIn the given circuit the voltage drop across the diode is 0.8 V, if the diode can withstand current upto maximum of 30 mA, then find the maximum voltage of the battery
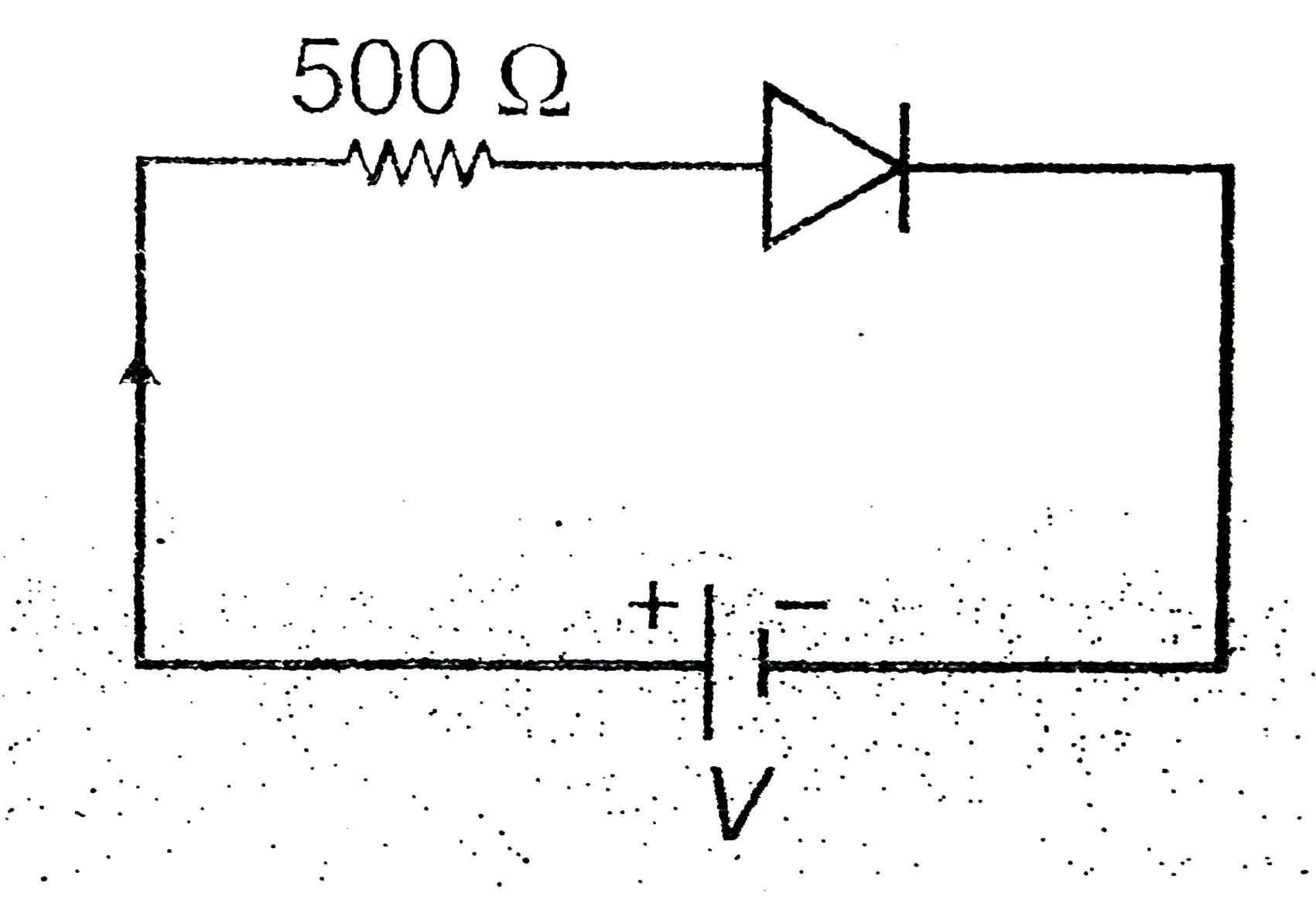
View SolutionIn u−v method to find focal length of a concave mirror, if object distance is found to be 10.0cm and image distance was also found to be 10.0cm, then find maximum permissible error in (f).
View Solution
