Two blocks of masses m1andm2(m1>m2) connected by a massless string passing over a frictionless pulley Magnitude of acceleration of blocks would be
(m1−m2m1+m2)g
(m1+m2m1−m2)g
(m2−m1m1+m2)g
(m2+m1m2−m1)g
To find the magnitude of acceleration of two blocks connected by a massless string over a frictionless pulley, we can follow these steps:
Step 1: Identify the forces acting on the blocks
- For block m1 (the heavier block), the forces acting on it are:
- Weight m1g acting downward
- Tension T acting upward
- For block m2 (the lighter block), the forces acting on it are:
- Weight m2g acting downward
- Tension T acting upward
Step 2: Write the equations of motion for each block
- For block m1:
m1g−T=m1a(1)
- For block m2:
T−m2g=m2a(2)
Step 3: Solve for tension T from equation (2)
Rearranging equation (2):
T=m2g+m2a(3)
Step 4: Substitute T from equation (3) into equation (1)
Substituting equation (3) into equation (1):
m1g−(m2g+m2a)=m1a
This simplifies to:
m1g−m2g−m2a=m1a
Step 5: Combine like terms
Rearranging gives:
m1g−m2g=m1a+m2a
Factoring out a on the right:
(m1−m2)g=(m1+m2)a
Step 6: Solve for acceleration a
Now, we can solve for a:
a=(m1−m2)g(m1+m2)
Conclusion
The magnitude of the acceleration of the blocks is:
a=(m1−m2)g(m1+m2)
---
- For block m1 (the heavier block), the forces acting on it are:
- Weight m1g acting downward
- Tension T acting upward
- For block m2 (the lighter block), the forces acting on it are:
- Weight m2g acting downward
- Tension T acting upward
- For block m1:
m1g−T=m1a(1)
- For block m2:
T−m2g=m2a(2)
Rearranging equation (2):
T=m2g+m2a(3)
Substituting equation (3) into equation (1):
m1g−(m2g+m2a)=m1a
This simplifies to:
m1g−m2g−m2a=m1a
Rearranging gives:
m1g−m2g=m1a+m2a
Factoring out a on the right:
(m1−m2)g=(m1+m2)a
Now, we can solve for a:
a=(m1−m2)g(m1+m2)
The magnitude of the acceleration of the blocks is:
a=(m1−m2)g(m1+m2)
Similar Questions
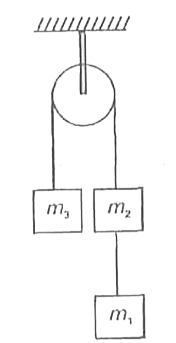
Three blocks of masses m1=4kg,m2=2kg,m3=4kg are connected with ideal strings passing over a smooth, massless pulley as shown in figure. The acceleration of blocks will be (g=10m/s2)
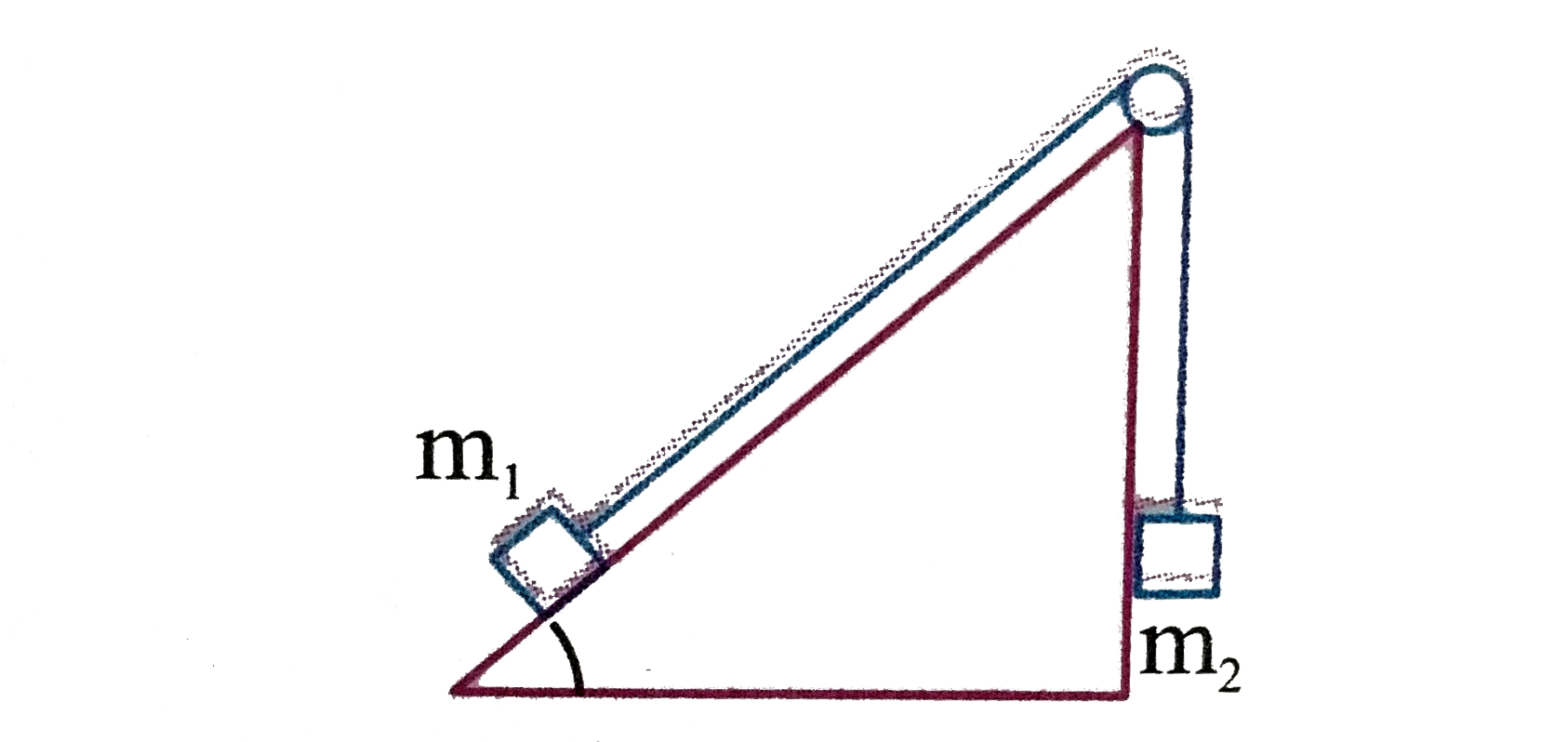
View SolutionTwo blocks of masses m1 and m2 are connected by a string of negligible mass which pass over a frictionless pulley fixed on the top of an inclined plane as shown in figure. The coefficient of friction between m1 and plane is μ.
View Solution
Knowledge Check
Two blocks of masses of 40 kg and 30 kg are connected by a weightless string passing over a frictionless pulley as shown in the figure.
 A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
A0.7ms−2B0.8ms−2C0.6ms−2D0.5ms−2
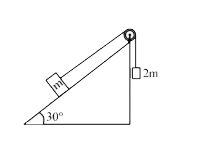
Two blocks of masses m and 2m are connected by a light string passing over a frictionless pulley. As shown in the figure, the mass m is placed on a smooth inclined plane of inclination 30° and 2m hangs vertically. If the system is released, the blocks move with an acceleration equal to :
View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View SolutionTwo masses m1 and m2(m2>m1) are hanging vertically over frictionless pulley. The acceleration of the two masses is :

View SolutionTwo blocks of masses 3 kg and 6 kg are connected by a string as shown in the figure over a frictionless pulley. The acceleration of the system is

A. 4m/s2
B. 2m/s2
C. zero
D. 6m/s2
View SolutionThree blocks of masses m1,m2and m3 are connected by massless strings as shown on a frictionless table. They are pulled with a force T3=40N. If m1=10kg,m2=6kg and m3=4kg the tension T2 will be

View SolutionTwo bodies of masses m1 and m2 are connected a light string which passes over a frictionless massless pulley. If the pulley is moving upward with uniform acceleration g2, then tension in the string will be
View SolutionTwo blocks of masses m1=4kg and m2=2kg are connected to the ends of a string which passes over a massless, frictionless pulley. The total downwards thrust on the pulley is nearly

View Solution
