A particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form :

$+ m v^{2} b \hat{k}$

$- m v b \hat{k}$

$- 2 m v b \hat{k}$

$- m v b \hat{j}$

Video Solution

Text Solution

Verified by Experts

The correct Answer is:B

Updated on:21/07/2023

Answer

Step by step video & image solution for A particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form : by Physics experts to help you in doubts & scoring excellent marks in Class 12 exams.

Updated on:21/07/2023

Class 12 PHYSICS SYSTEM OF PARTICLES AND ROTATIONAL MOTION

Knowledge Check

A mass M moving with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin
Aa. is zero
Bb. remains constant
Cc. goes on increasing
Dd. goes on decreasing

A particle of mass m is moving with constant velocity v parallel to the x-axis as shown in the figure. Its angular momentum about origin O is

View Solution
A particle mass parallel to x-axis with constant velocity $v$ as shown in the figure. The angular velocity of the particle about the origin O

View Solution
On a frictionless horizontal surface , assumed to be the $x - y$ plane , a small trolley $A$ is moving along a straight line parallel to the $y$ -axis( see figure) with a constant velocity of $(\sqrt{3} - 1) m / s$ . At a particular instant , when the line $O A$ makes an angle of $45 (\circ)$ with the $x$ - axis , a ball is thrown along the surface from the origin $O$ . Its velocity makes an angle $ϕ$ with the $x$ -axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle $θ$ made by the velocity vector of the ball with the $x$ -axis in this frame .
(b) Find the speed of the ball with respect to the surface , if $ϕ = (4 θ) / (3)$ .

View Solution
A particle moves on a straight line with a uniform velocity. It's angular momentum
View Solution
On a frictionless horizontal surface , assumed to be the $x - y$ plane , a small trolley $A$ is moving along a straight line parallel to the $y -$ axis ( see figure) with a constant velocity of $(\sqrt{3} - 1) m / s$ . At a particular instant , when the line $O A$ makes an angle of $45 (\circ)$ with the $x -$ axis , a ball is thrown along the surface from the origin $O$ . Its velocity makes an angle $ϕ$ with the $x -$ axis and it hits the trolley .
(a) The motion of the ball is observed from the frame of the trolley . Calculate the angle $θ$ made by the velocity vector of the ball with the $x -$ axis in this frame .
(b) Find the speed of the ball with respect to the surface , if $ϕ = (4 θ) / (3)$ .

View Solution
A particle is moving parallel to x-axis as shown in the figure. The angular velocity of the particle about the origin is
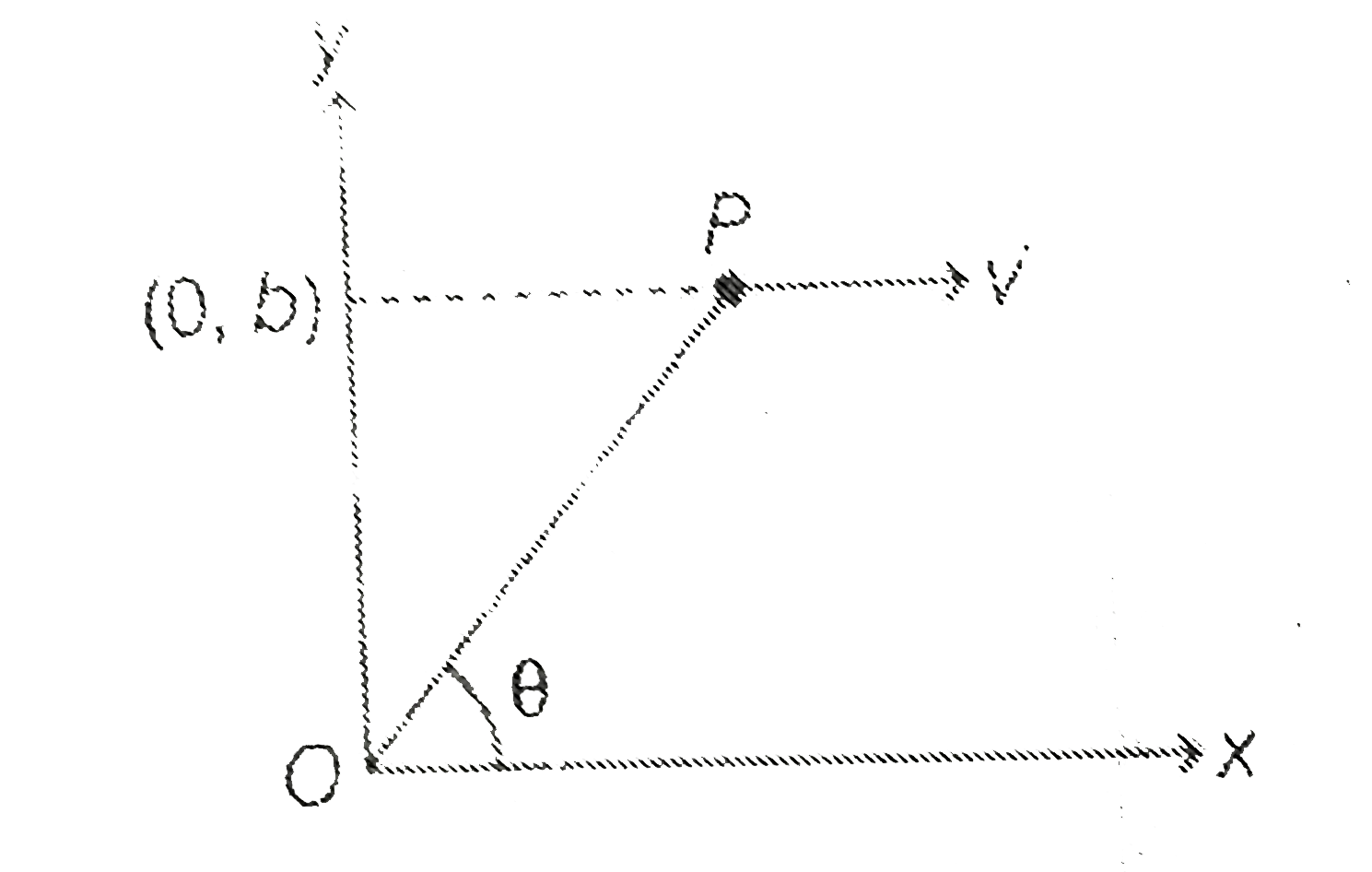
View Solution
A particle of mass $m = 3 k g$ moves along a straight line $4 y - 3 x = 2$ where $x$ and $y$ are in metre, with constant velocity $v = 5 m s^{- 1}$ the magnitude of angular momentum about the origin is
View Solution

A particle is moving along a straight line parallel to x-axis with constant velocity. Find angular momentum about the origin in vector form :

The correct Answer is:B

Similar Questions

Knowledge Check

A mass M moving with a constant velocity parallel to the X-axis. Its angular momentum with respect to the origin

Recommended Questions