A meter stick is held vertically with one end on the floor and is allowed to fall. The speed of the other end when it hits the floor assuming that the end at the floor does not slip is (g=9.8m/s2)
3.2 m/s
5.4 m/s
7.6 m/s
9.2 m/s
The correct Answer is:B
To find the speed of the other end of the meter stick when it hits the floor, we can follow these steps:
Step 1: Understand the system
We have a vertical meter stick (length = 1 meter) that is pivoted at one end (point O) and allowed to fall. The other end (point A) will move in a circular arc around point O.
Step 2: Identify the energy states
Initially, when the stick is vertical, it has potential energy and no kinetic energy. When the stick falls and the end A hits the floor, it has kinetic energy and no potential energy.
Step 3: Write the conservation of energy equation
Using the principle of conservation of mechanical energy:
UA+KA=UB+KB
Where:
- UA = Initial potential energy at position A
- KA = Initial kinetic energy at position A
- UB = Final potential energy at position B
- KB = Final kinetic energy at position B
Step 4: Calculate initial potential energy
The height of the center of mass of the stick when it is vertical is h=12 meter (0.5 m). Thus, the initial potential energy is:
UA=mgh=mg⋅0.5
Step 5: Calculate final potential energy
When the stick is horizontal, the height of the center of mass is 0, so:
UB=0
Step 6: Calculate initial and final kinetic energy
Initially, the kinetic energy KA is 0 because the stick is at rest. When the stick is horizontal, the kinetic energy can be expressed as rotational kinetic energy about point O:
KB=12Iω2
Where I is the moment of inertia of the stick about point O, and ω is the angular velocity.
Step 7: Calculate the moment of inertia
The moment of inertia I of a meter stick about one end is given by:
I=13mL2=13m(12)=13m
Step 8: Substitute into the energy equation
Now substituting into the energy conservation equation:
mg⋅0.5+0=0+12(13m)ω2
Step 9: Simplify the equation
Cancelling m from both sides (assuming m≠0):
g⋅0.5=16ω2
ω2=3g
ω=√3g
Step 10: Calculate the speed of the end A
The speed V of the end A when it hits the floor is given by:
V=Rω
Where R=1 meter (the length of the stick).
Thus:
V=1⋅√3g=√3⋅9.8
Step 11: Calculate the numerical value
Calculating V:
V=√29.4≈5.42m/s
Conclusion
The speed of the other end of the meter stick when it hits the floor is approximately 5.42m/s.
---
We have a vertical meter stick (length = 1 meter) that is pivoted at one end (point O) and allowed to fall. The other end (point A) will move in a circular arc around point O.
Initially, when the stick is vertical, it has potential energy and no kinetic energy. When the stick falls and the end A hits the floor, it has kinetic energy and no potential energy.
Using the principle of conservation of mechanical energy:
UA+KA=UB+KB
Where:
- UA = Initial potential energy at position A
- KA = Initial kinetic energy at position A
- UB = Final potential energy at position B
- KB = Final kinetic energy at position B
The height of the center of mass of the stick when it is vertical is h=12 meter (0.5 m). Thus, the initial potential energy is:
UA=mgh=mg⋅0.5
When the stick is horizontal, the height of the center of mass is 0, so:
UB=0
Initially, the kinetic energy KA is 0 because the stick is at rest. When the stick is horizontal, the kinetic energy can be expressed as rotational kinetic energy about point O:
KB=12Iω2
Where I is the moment of inertia of the stick about point O, and ω is the angular velocity.
The moment of inertia I of a meter stick about one end is given by:
I=13mL2=13m(12)=13m
Now substituting into the energy conservation equation:
mg⋅0.5+0=0+12(13m)ω2
Cancelling m from both sides (assuming m≠0):
g⋅0.5=16ω2
ω2=3g
ω=√3g
The speed V of the end A when it hits the floor is given by:
V=Rω
Where R=1 meter (the length of the stick).
Thus:
V=1⋅√3g=√3⋅9.8
Calculating V:
V=√29.4≈5.42m/s
The speed of the other end of the meter stick when it hits the floor is approximately 5.42m/s.
Similar Questions
A thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. Find the velocity of the other end when it hits the floor, assuming that the end on the floor does not slip?
View SolutionA thin rod of length L and mass M is held vertically with one end on the floor and is allowed to fall. Find the velocity of the other end when it hits the floor, assuming that the end on the floor does not slip?
View SolutionThe one end of a 20 m long ladder is on the floor and the other end is in the contact of vertical wall. Its lower end slides on the floor. Show that the rate of sliding of the upper end is 4/3 times the rate of sliding the lower end when the lower end is 16 m away from the wall.
View SolutionA thin rod of mass m and length l is hinged at the lower end to a level floor and stands vertically. Then its upper end will strike the floor with a velocity given by:
View SolutionWater drops fall from a tap on to the floor 5.0 m below at regular intervals of time. The first drop strikes the floor when the fifth drops beings to fall. The height at which the third drop will be from ground at the instant when the first drop strikes the ground is (takeg=10m−2)
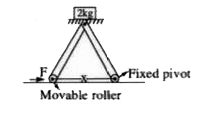
View SolutionThe machine as shown has 2 rods of length 1 m connected by a pivot at the top. The end of one rod is connected to the floor by a stationary pivot and the end of the other rod has a roller that rolls along the floor in a slot. As the roller goes back and forth, a 2 kg weight moves up and down. If the roller is moving towards right at a constant speed, the weight moves up with a
View SolutionA line is of length 10 units and one of its ends is (−2,3). If the ordinate of the other end is 9, prove that the abscissa of the other end is 6 or −10
View SolutionA ball of mass 2 kg is gently pushed off the edge of a tabletop that is 1.8 m above the floor. Find the speed of the ball as it strikes the floor.
View SolutionA very broad elevator is going up vertically with a constant acceleration of 2m/s2. At the instant when its velocity is 4m/s a ball is projected form the floor of the lift with a speed of 4m/s relative to the floor at an elevation of 30∘. Time taken by the ball to return the floor is (g=10ms2)
View SolutionA very broad elevator is going up vertically with a constant acceleration of 2m/s2. At the instant when its velocity is 4m/s a ball is projected form the floor of the lift with a speed of 4m/s relative to the floor at an elevation of 30∘. Time taken by the ball to return the floor is (g=10ms2)
View Solution