A circular disc of mass 2 kg and radius 10 cm rolls without slipping with a speed 2 m/s. The total kinetic energy of disc is
10 J
6 J
2 J
4 J
The correct Answer is:B
To find the total kinetic energy of the circular disc, we need to consider both its translational and rotational kinetic energy. Here’s a step-by-step solution:
Step 1: Identify the given values
- Mass of the disc (m) = 2 kg
- Radius of the disc (R) = 10 cm = 0.1 m (convert cm to m)
- Speed of the disc (V) = 2 m/s
Step 2: Calculate the translational kinetic energy (TKE)
The formula for translational kinetic energy is:
TKE=12mV2
Substituting the values:
TKE=12×2kg×(2m/s)2
TKE=12×2×4=4J
Step 3: Calculate the rotational kinetic energy (RKE)
For a disc rolling without slipping, the relationship between linear speed (V) and angular speed (ω) is given by:
V=Rω⇒ω=VR
Now, the moment of inertia (I) of a disc about its center is:
I=12mR2
Substituting the values:
I=12×2kg×(0.1m)2=12×2×0.01=0.01kg m2
Now, substituting ω in the formula for rotational kinetic energy:
RKE=12Iω2
Substituting ω:
RKE=12×0.01kg m2×(2m/s0.1m)2
Calculating ω:
ω=20.1=20rad/s
Now substituting ω back:
RKE=12×0.01×(20)2=12×0.01×400=2J
Step 4: Calculate the total kinetic energy (TKE + RKE)
Total Kinetic Energy=TKE+RKE=4J+2J=6J
Final Answer
The total kinetic energy of the disc is 6 Joules.
---
- Mass of the disc (m) = 2 kg
- Radius of the disc (R) = 10 cm = 0.1 m (convert cm to m)
- Speed of the disc (V) = 2 m/s
The formula for translational kinetic energy is:
TKE=12mV2
Substituting the values:
TKE=12×2kg×(2m/s)2
TKE=12×2×4=4J
For a disc rolling without slipping, the relationship between linear speed (V) and angular speed (ω) is given by:
V=Rω⇒ω=VR
Now, the moment of inertia (I) of a disc about its center is:
I=12mR2
Substituting the values:
I=12×2kg×(0.1m)2=12×2×0.01=0.01kg m2
Now, substituting ω in the formula for rotational kinetic energy:
RKE=12Iω2
Substituting ω:
RKE=12×0.01kg m2×(2m/s0.1m)2
Calculating ω:
ω=20.1=20rad/s
Now substituting ω back:
RKE=12×0.01×(20)2=12×0.01×400=2J
Total Kinetic Energy=TKE+RKE=4J+2J=6J
The total kinetic energy of the disc is 6 Joules.
Similar Questions
A uniform circular disc of mass M and radius R rolls without slipping on a horizontal surface. If the velocity of its centre is v0, then the total angular momentum of the disc about a fixed point P at a height (3R)/2 above the centre C.

View SolutionA sphere of mass 50 gm and diameter 2 cm rolls without slipping with a velocfty of 5 cm/s. Calculate the total energy.
View SolutionA loop and a disc have same mass and roll without slipping with the same linear velocity v. If the total kinetic energy of the loop is 8J, the kinetic energy of the disc must be.
View SolutionA circular disc of 49 kg and radius 50 cm is rotating at a speed of 120 rotations per minute. Calculate its kinetic energy if is moment of inertia about the axis of rotation is 12mr2.
View SolutionA circular disc of mass M and radius R is rotating about its axis with angular speed If about another stationary disc having radius ω1.
R2 and same mass M is dropped co- axially on to the rotating disc. Gradually both discs attain constant angular speed ω2. The energy lost in the process is p% of the initial energy . Value of p is ........
View SolutionA disc of mass m and radius R is rolling without slipping as shown in the figure. The magnitude of net velocity of the point P is (OP=R2)
View SolutionA solid sphere of mas 2kg rolls on a table with linear speed of 1m/s. Its total kinetic energy is
View Solution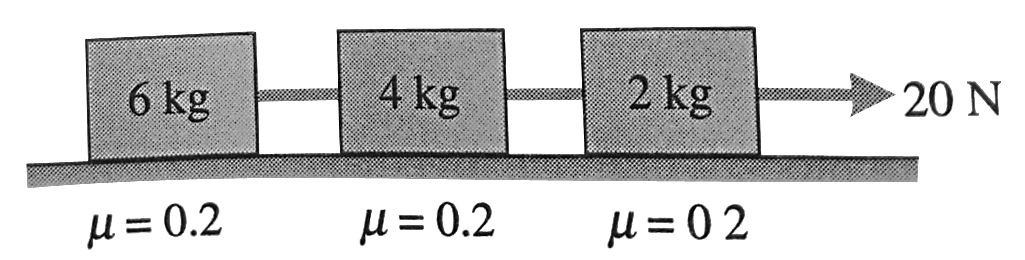
Three blocks of masses 6 kg, 4 kg and 2 kg are pulled on a rough surface by applying a constant force 20 N. The values of coefficient of friction between blocks and suface are shown in figure.
Q. In the arrangement shoen tension in the string connecting 4 kg and 6 kg masses is
View SolutionWork energy theorem sys"work done by all the force is equal to change in kinetic energy" In the diagram, a disc of mass M and radius Ris rolling without slipping on a rough fixed inclined AB=l,V= velocity of disc at B.
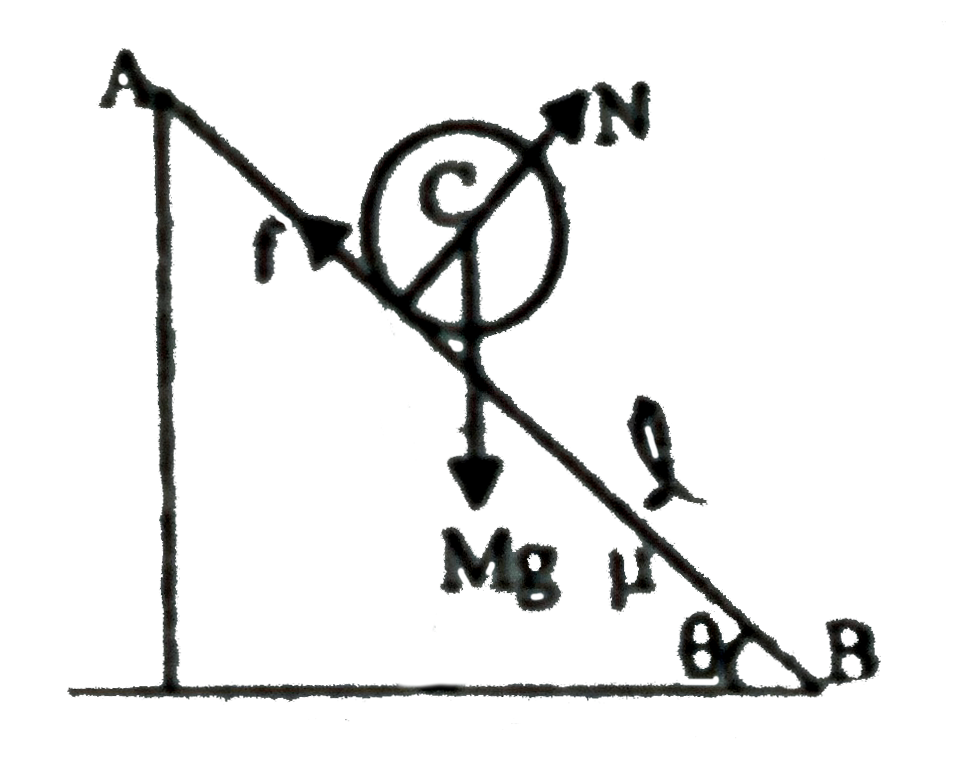
Choose the correct option(s)
View SolutionWork energy theorem sys work done by all the force is equal to change in kinetic energy" In the diagram, a disc of mass M and radius Ris rolling without slipping on a rough fixed inclined AB=l,V= velocity of disc at B.
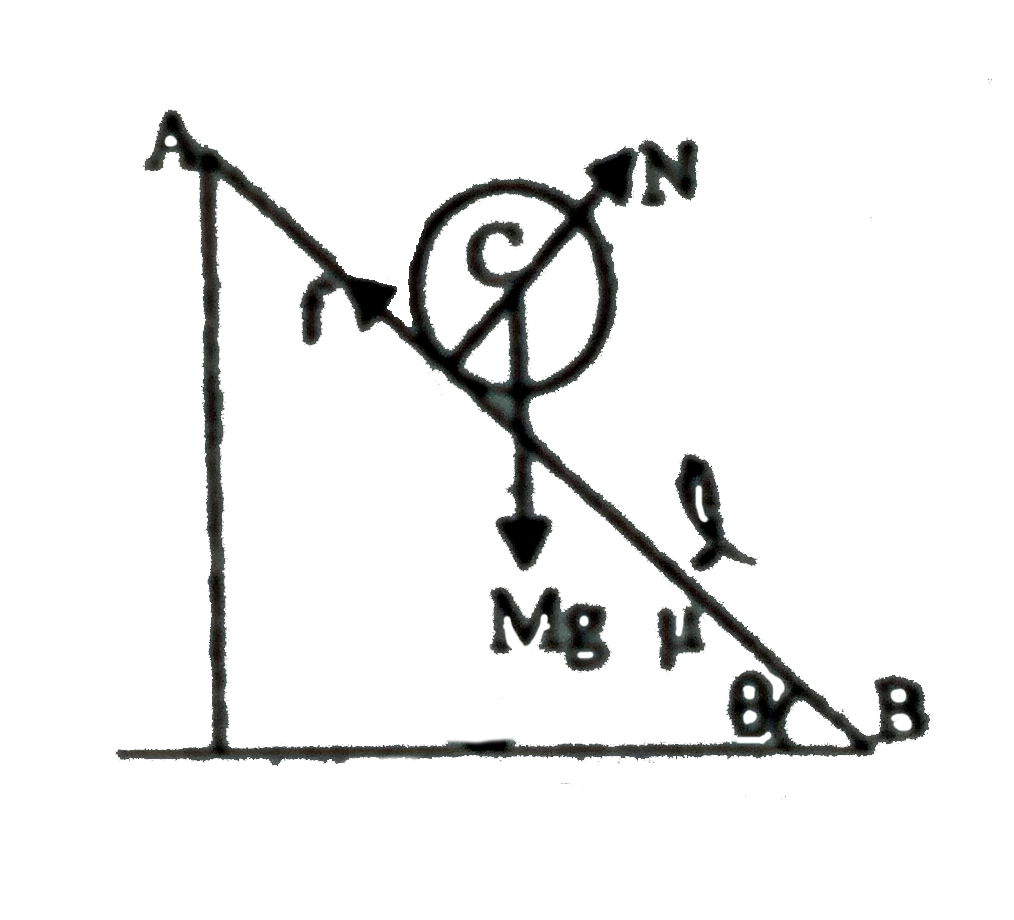
Choose the correct option(s)
View Solution