A : It is very difficult to open or close a door if force is applied near the hinge.
R : The moment of applied force is minimum near the hinge.
If both Assertion & Reason are true and the reason is the correct explanation of the assertion,
If both Assertion & Reason are true but the reason is not the correct explanation of the assertion,
If Assertion is true statement but Reason is false,
If both Assertion and Reason are false statements,
The correct Answer is:A
To solve the question regarding the difficulty of opening or closing a door when force is applied near the hinge, we will analyze the concepts of torque and the moment of force.
1. Understanding Torque:
- Torque (τ) is defined as the product of the force (F) applied and the distance (R) from the pivot point (hinge) to the point where the force is applied. Mathematically, it is expressed as:
τ=R×F
- Here, R is the perpendicular distance from the line of action of the force to the pivot point (hinge).
2. Force Application Near the Hinge:
- When a force is applied near the hinge, the distance R is small. This results in a smaller torque since:
τ=R×F(with small R)
- Therefore, the torque is minimized when the force is applied close to the hinge.
3. Difficulty in Opening the Door:
- Since torque is the turning force, a smaller torque means it requires more effort to turn the door. Thus, it becomes difficult to open or close the door when the force is applied near the hinge.
4. Force Application Away from the Hinge:
- Conversely, when the force is applied farther from the hinge, R increases. This leads to a larger torque:
τ=R×F(with larger R)
- A larger torque makes it easier to open or close the door.
5. Conclusion:
- Statement A is correct: It is indeed very difficult to open or close a door if force is applied near the hinge.
- Statement R is also correct: The moment of applied force (torque) is minimum near the hinge because the distance R is small.
6. Final Answer:
- Both statements A and R are correct, and R provides the correct explanation for A.
- Torque (τ) is defined as the product of the force (F) applied and the distance (R) from the pivot point (hinge) to the point where the force is applied. Mathematically, it is expressed as:
τ=R×F
- Here, R is the perpendicular distance from the line of action of the force to the pivot point (hinge).
- When a force is applied near the hinge, the distance R is small. This results in a smaller torque since:
τ=R×F(with small R)
- Therefore, the torque is minimized when the force is applied close to the hinge.
- Since torque is the turning force, a smaller torque means it requires more effort to turn the door. Thus, it becomes difficult to open or close the door when the force is applied near the hinge.
- Conversely, when the force is applied farther from the hinge, R increases. This leads to a larger torque:
τ=R×F(with larger R)
- A larger torque makes it easier to open or close the door.
- Statement A is correct: It is indeed very difficult to open or close a door if force is applied near the hinge.
- Statement R is also correct: The moment of applied force (torque) is minimum near the hinge because the distance R is small.
- Both statements A and R are correct, and R provides the correct explanation for A.
Similar Questions
Knowledge Check
the work done by applied force is
A10 JB50 JC100 JD150 J
When a force is applied on an object and if the body moves in the direction of applied force, work is said to be done.
View Solution
Where is the force usually applied in Figure 1 ?
View SolutionA rod AB of mass M and length L is shown in figure. End A of rod is hinged and end B is lying on the ground. Find the Vertical component of the force applied by the hinge
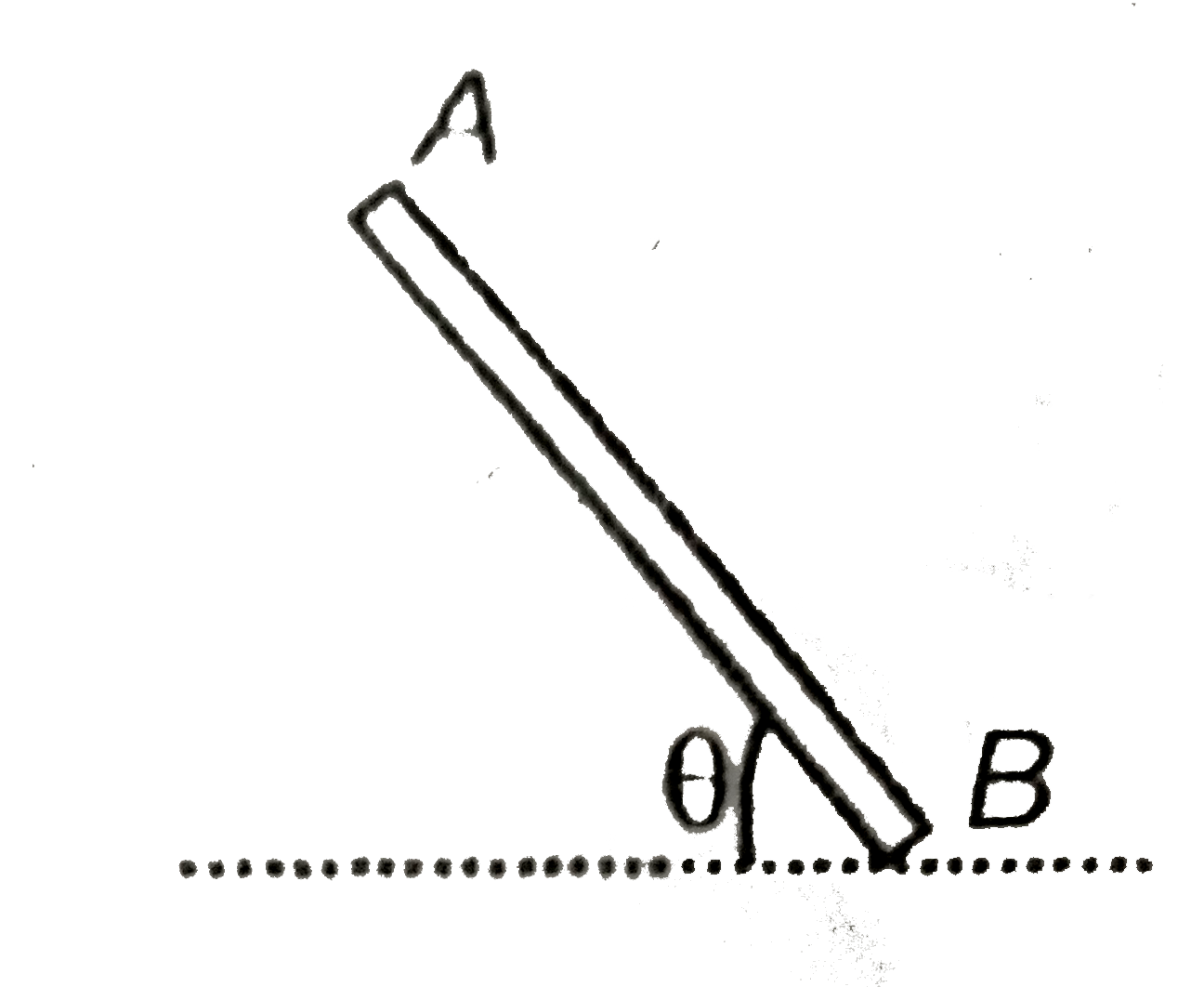
Vertical component of the force applied by the hinge
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
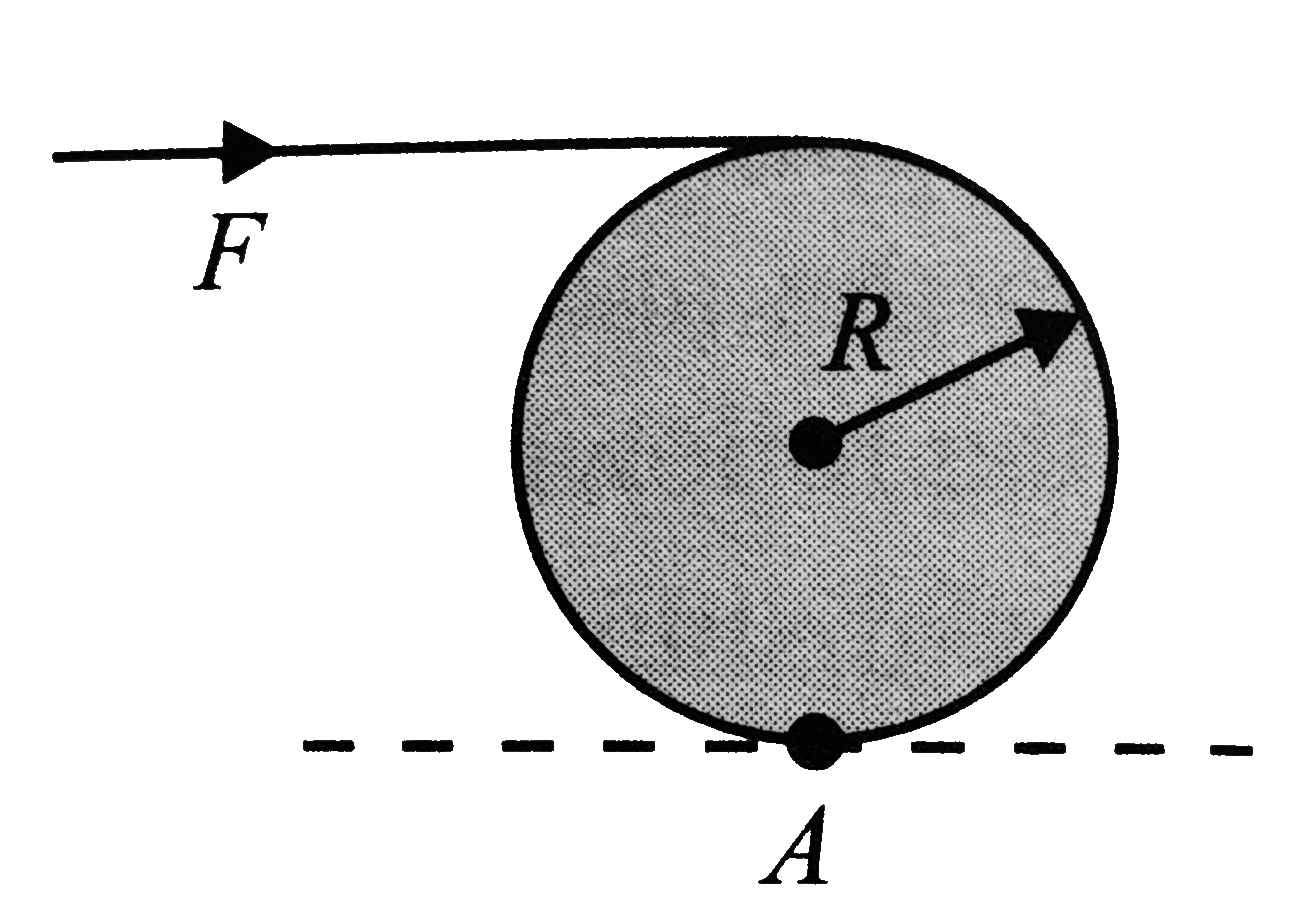
Component of reaction at the hinge in the horizontal direction is
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
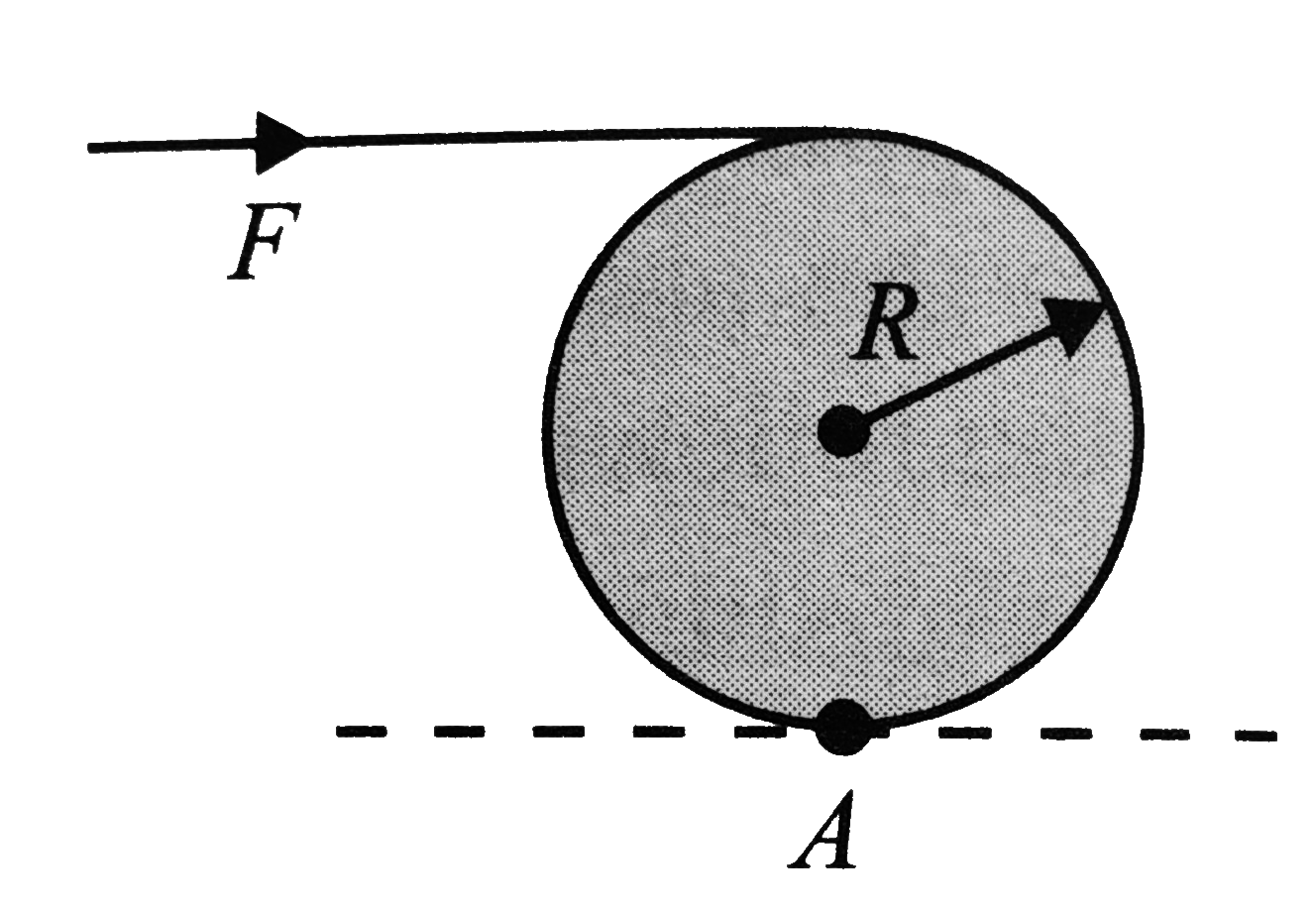
Component of reaction at the hinge in the vertical direction is
View SolutionWhen a body is hinged at a point and a force is acting on the body in such a way that the line of action of force is at some distance from the hinged point, the body will start rotating about the hinged point. The angular acceleration of the body can be calculated by finding the torque of that force about the hinged point. A disc of mass m and radius R is hinged at point A at its bottom and is free to rotate in the vertical plane. A force of magnitude F is acting on the ring at top most point.
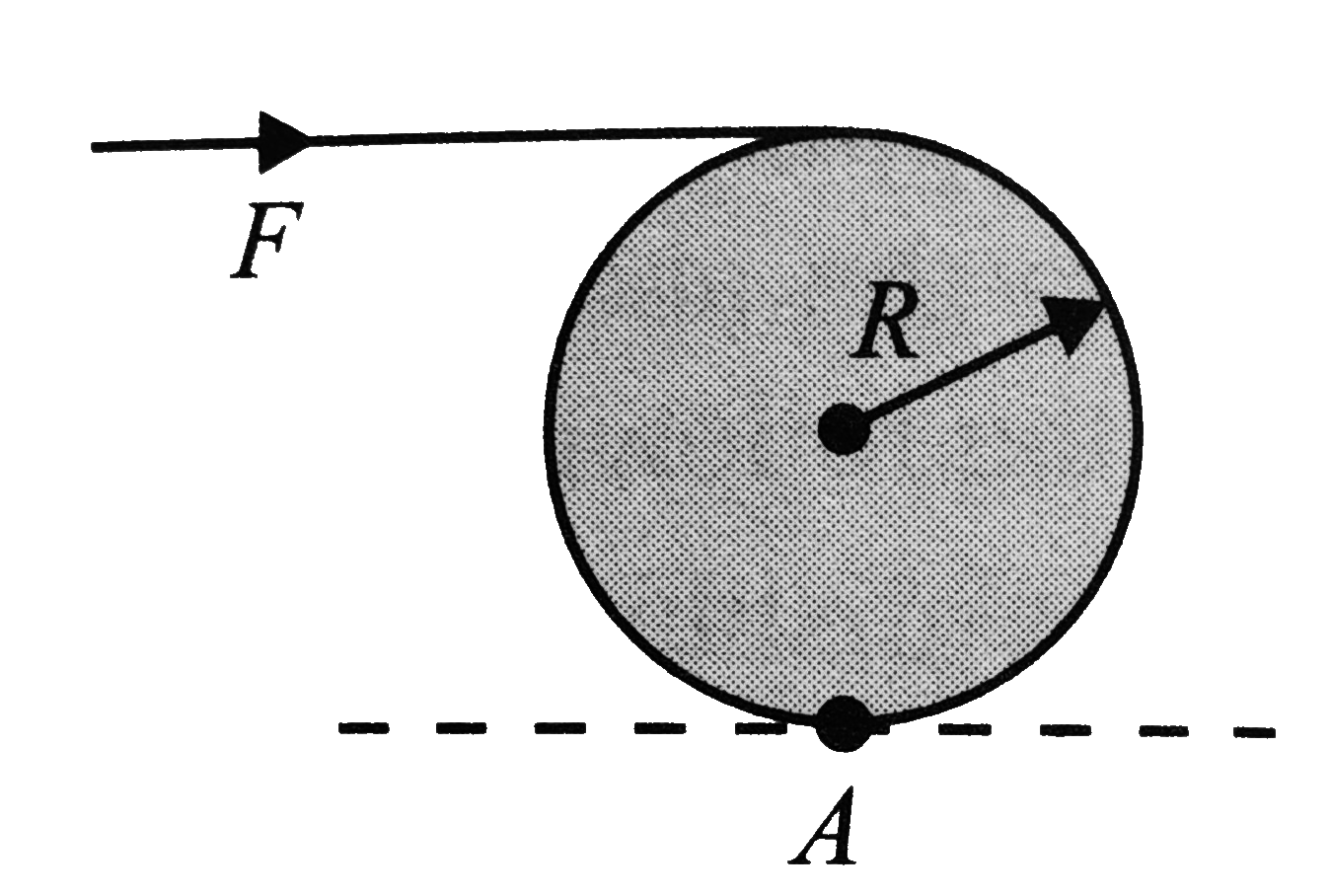
Tangential acceleration of the centre of mass is
View SolutionIs it possible that the restoring force is not equal and opposite to the applied force?
View Solution
